Замена переменных в тройном интеграле
Теорема о замене переменных в тройном интеграле
Пусть в пространстве $\mathbf { \textit { Ouvw } } $ задана область $\mathbf { \textit { G } } $, и пусть отображение $F(M)=M^\ast $ преобразует эту область в область $\mathbf { \textit { V } } $ пространства $\mathbf { \textit { Oxyz } } . $ Будем считать, что отображение $\mathbf { \textit { F } } $ задаётся функциями $F:\left[{ \begin{array} { l } x=x(u,v,w) \\ y=y(u,v,w) \\ z=z(u,v,w) \\ \end{array} }\right.$.
Пусть:
- $\mathbf { \textit { F } } $ взаимно однозначно отображает $\mathbf { \textit { G } } $ на $\mathbf { \textit { V } } $;
- Функции $\mathbf { \textit { x } } (\mathbf { \textit { u,v,w } } )\mathbf { \textit { , y } } (\mathbf { \textit { u,v,w } } ), \mathbf { \textit { z(u,v,w) } } $ непрерывно дифференцируемы на $\mathbf { \textit { G } } $ { имеют непрерывные частные производные } ;
-
Якобиан $J(u,v,w)=\frac { \partial (x,y,z) } { \partial (u,v,w) } =\left| { \begin{array} { l } \frac { \partial x } { \partial u } \quad \frac { \partial y } { \partial u } \quad \frac { \partial z } { \partial u } \\ \frac { \partial x } { \partial v } \quad \frac { \partial y } { \partial v } \quad \frac { \partial z } { \partial v } \\ \frac { \partial x } { \partial w } \quad \frac { \partial y } { \partial w } \quad \frac { \partial z } { \partial w } \\ \end{array} }\right|$ не обращается в нуль на $\mathbf { \textit { G } } .$
Тогда $\iiint\limits_V { f(x,y,z)dxdydz } =\iiint\limits_G { f(x(u,v,w),y(u,v,w),z(u,v,w))\cdot \left| { J(u,v,w) }\right|\cdot dudvdw } $.
Доказательство этой теоремы аналогично доказательству теоремы о замене переменных в двойном интеграле.
Рассмотрим наиболее часто употребляемые криволинейные системы координат в пространстве - цилиндрические и сферические.
Тройной интеграл в цилиндрических координатах
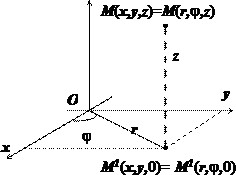
В этой координатной системе положение точки в пространстве характеризуется тремя числами: $\mathbf { \textit { r } } $, $\varphi $ и $\mathbf { \textit { z } } $, где $\mathbf { \textit { r } } $ и $\varphi $ - полярные координаты проекции $\mathbf { \textit { M } } ^ { 1 } $
точки $\mathbf { \textit { М } } $ на плоскость$\mathbf { \textit { Оху } } $, $\mathbf { \textit { z } } $ - аппликата точки $\mathbf { \textit { M } } $. Формулы перехода от цилиндрических координат к декартовым: $ \begin{array} { l } x=r\cos \varphi , \\ y=r\sin \varphi , \\ z=z. \\ \end{array} $
Вычислим якобиан этого преобразования: $J(r,\varphi ,z)=\left| { \begin{array} { l } \frac { \partial x } { \partial r } \quad \frac { \partial y } { \partial r } \quad \frac { \partial z } { \partial r } \\ \frac { \partial x } { \partial \varphi } \quad \frac { \partial y } { \partial \varphi } \quad \frac { \partial z } { \partial \varphi } \\ \frac { \partial x } { \partial z } \quad \frac { \partial y } { \partial z } \quad \frac { \partial z } { \partial z } \\ \end{array} }\right|=\left| { \begin{array} { l } \cos \varphi \quad -r\sin \varphi \quad 0 \\ \sin \varphi \quad \;\;r\cos \varphi \quad 0 \\ \;\;0\;\;\;\;\;\;\quad 0\;\;\;\;\;\quad 1 \\ \end{array} }\right|=r$, следовательно, $\iiint\limits_V { f(x,y,z)dxdydz } =\iiint\limits_V { f(r\cos \varphi ,r\sin \varphi ,z)\cdot r\cdot drd\varphi dz } $.
Тройной интеграл в сферических координатах
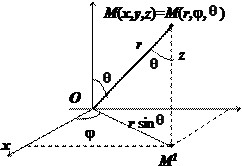
В этих координатах положение точки $\mathbf { \textit { M } } $ в пространстве характеризуется тремя числами: $\mathbf { \textit { r } } $, $\varphi $ и $\theta $, где $\mathbf { \textit { r } } $ - длина радиуса-вектора точки $\mathbf { \textit { M } } $, $\varphi $ - полярный угол проекции $\mathbf { \textit { M } } ^ { 1 } $точки $\mathbf { \textit { М } } $ на плоскость$\mathbf { \textit { Оху } } $, $\theta $ - угол между радиусом-вектором точки $\mathbf { \textit { M } } $ и осью $\mathbf { \textit { Oz } } $. Формулы перехода от сферических координат к декартовым: $ \begin{array} { l } x=r\sin \theta \cos \varphi , \\ y=r\sin \theta \sin \varphi , \\ z=r\cos \theta . \\ \end{array} $
Вычислим якобиан этого преобразования:
$=\left| { \begin{array} { l } \;\;\sin \theta \cos \varphi \quad \;\;\;\;\;\sin \theta \sin \varphi \;\;\quad \cos \theta \\ -r\sin \theta \sin \varphi \quad \;\;r\sin \theta \cos \varphi \;\;\;\;\;\quad 0 \\ \;\;r\cos \theta \cos \varphi \quad r\cos \theta \sin \varphi \;\;-r\sin \theta \\ \end{array} }\right|=r^2\sin \theta \left| { \begin{array} { l } \sin \theta \cos \varphi \;\;\;\;\sin \theta \sin \varphi \;\;\quad \cos \theta \\ \;-\sin \varphi \quad \;\;\;\;\cos \varphi \;\;\;\;\;\;\;\;\;\quad 0 \\ \cos \theta \cos \varphi \quad \cos \theta \sin \varphi \;\;-\sin \theta \\ \end{array} }\right|= \\ =r^2\sin \theta \left[ { \cos \theta (-\cos \theta \sin ^2\varphi -\cos \theta \cos ^2\varphi )-\sin \theta (\sin \theta \cos ^2\varphi +\sin \theta \sin ^2\varphi ) }\right]=-r^2\sin \theta ,$ следовательно, $\iiint\limits_V { f(x,y,z)dxdydz } =\iiint\limits_ { V_ { r,\varphi ,\theta } } { f(r\sin \theta \cos \varphi ,r\sin \theta \sin \varphi ,r\cos \theta )\cdot r^2\sin \theta \cdot drd\varphi d\theta } $.
Далее:
Определение криволинейного интеграла второго рода
Вычисление двойного интеграла
Равносильные формулы алгебры высказываний
Класс $T_1$. Теорема о замкнутости класса $T_1$
Лемма о построении множества $[F]_{x1,x2}$
Нахождение потенциала
Примеры применения цилиндрических и сферических координат
Логические операции над высказываниями
Класс $L$. Теорема о замкнyтости класса $L$
Инвариантное определение дивергенции
Введение
Линейный интеграл и циркуляция векторного поля
Критерий полноты {формулировка}. Лемма о несамодвойственной функции
Теорема Остроградского
Огравление $\Rightarrow $
Комментарии ()