Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному
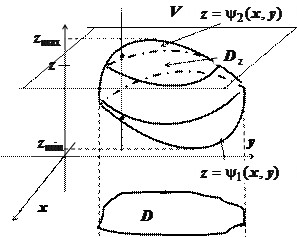
Будем называть ограниченную замкнутую область $\mathbf { \textit { V } } \textbf { простой правильной } $, если выполняются два условия : проекция $\mathbf { \textit { V } } $ на какую-либо координатную плоскость, например, на плоскость $\mathbf { \textit { Оху } } $ - простая область $\mathbf { \textit { D } } $, и любая прямая, перпендикулярная этой плоскости и проходящая через внутреннюю точку $\mathbf { \textit { V } } $, пересекает границу $\mathbf { \textit { V } } $ в двух точках. Такую область можно описать следующим образом: $V=\left( { (x,y,z)\vert (x,y)\in D,\;\psi _1 (x,y)\leqslant z\leqslant \psi _2 (x,y) }\right)$ поверхность $z=\psi _1 (x,y)$ образована множеством нижних точек пересечения прямой, параллельной оси$\mathbf { \textit { Oz } } $, с границей $\mathbf { \textit { V } } $; поверхность $z=\psi _2 (x,y)$ - множеством верхних точек пересечения).
Теорема
Если $\mathbf { \textit { V } } $ - простая область с кусочно-гладкой границей, $\mathbf { \textit { f } } (\mathbf { \textit { P } } )$ - непрерывная функция, то $\iiint\limits_V { f(P)dv } =\iint\limits_D { dxdy\int\limits_ { \psi _1 (x,y) } ^ { \psi _2 (x,y) } { f(x,y,z)dz } } $.
$\textbf { Доказать } $эту теорему можно так, как мы доказали теорему о переходе от двойного интеграла к повторному: установить, что для повторного интеграла в правой части формулы имеют место все свойства интеграла, разбить область $\mathbf { \textit { V } } $ на подобласти $\mathbf { \textit { V } } _ { i } (\mathbf { \textit { i } } = 1,2, { \ldots } ,\mathbf { \textit { n } } )$, пользуюсь свойствами аддитивности и теоремой о среднем, представить повторный интеграл как интегральную сумму для тройного $\left( { \sum\limits_ { i=1 } ^n { f(P_i )v(V_i ) } }\right)$ и перейти к пределу при $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n } diam(V_i )\to 0$.
Если расписать двойной интеграл по простой области $\mathbf { \textit { D } } \quad \left( { D=\left[{ (x,y)\left| { \begin{array} { l } a\leqslant x\leqslant b, \\ \varphi _1 (x)\leqslant y\leqslant \varphi _2 (x) \\ \end{array} }\right. }\right] }\right)$ в виде повторного, получим ещё более детализированную формулу для вычисления тройного интеграла: $\iiint\limits_V { f(P)dv } =\iint\limits_D { dxdy\int\limits_ { \psi _1 (x,y) } ^ { \psi _2 (x,y) } { f(x,y,z)dz } } =\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { dy\int\limits_ { \psi _1 (x,y) } ^ { \psi _2 (x,y) } { f(x,y,z)dz } } } $.
Можно также доказать, что тройной интеграл можно представить в виде повторного с другим порядком интегрирования. Обозначим $z_ { \min } =\mathop { \min z } \limits_ { (x,y,z)\in V } ,\;z_ { \max } =\mathop { \max z } \limits_ { (x,y,z)\in V } $ т.е. минимальное и максимальное значения ординаты для точек области $\mathbf { \textit { V } } )$, $D_z $ - плоскую область, получающуюся при сечении $\mathbf { \textit { V } } $ плоскостью $\mathbf { \textit { z } } $ = const. Тогда $\iiint\limits_V { f(P)dv } =\int\limits_ { z_ { \min } } ^ { z_ { \max } } { dz\iint\limits_ { D_z } { f(x,y,z) } } dxdy$. Естественно, для конкретной задачи может оказаться предпочтительней проектировать $\mathbf { \textit { V } } $ не на плоскость $\mathbf { \textit { Оху } } $, а на другую координатную плоскость.
Примеры решения задач
Пример 1
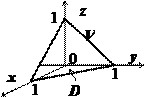
$I=\iiint\limits_V { \frac { dxdydz } { \left( { 1+x+y+z }\right)^3 } } ,\;V:\left[{ \begin{array} { l } x=0,\;y=0,\;z=0, \\ x+y+z=1. \\ \end{array} }\right.$
Проекция области $\mathbf { \textit { V } } $ на плоскость $\mathbf { \textit { Оху } } $ - треугольник $D:\left[{ x=0,\;y=0,\;x+y=1 }\right]$, поэтому $I=\iiint\limits_V { \frac { dxdydz } { \left( { 1+x+y+z }\right)^3 } } =\iint\limits_D { dxdy\int\limits_0^ { 1-x-y } { \frac { dz } { (1+x+y+z)^3 } } } =\iint\limits_D { \left. { \left[ { -\frac { 1 } { 2 } \cdot \frac { 1 } { (1+x+y+z)^2 } }\right] }\right|_0^ { 1-x-y } dxdy } =$
$=-\frac { 1 } { 2 } \int\limits_0^1 { dx } \int\limits_0^ { 1-x } { \left[ { \frac { 1 } { 4 } -\frac { 1 } { (1+x+y)^2 } }\right]dy } =-\frac { 1 } { 2 } \int\limits_0^1 { \left. { \left[ { \frac { y } { 4 } +\frac { 1 } { 1+x+y } }\right] }\right|_0^ { 1-x } dx } =-\frac { 1 } { 2 } \int\limits_0^1 { \left[ { \frac { 1-x } { 4 } +\frac { 1 } { 2 } -\frac { 1 } { 1+x } }\right]dx } = \\ =-\frac { 1 } { 2 } \int\limits_0^1 { \left[ { \frac { 1-x } { 4 } +\frac { 1 } { 2 } -\frac { 1 } { 1+x } }\right]dx } =-\frac { 1 } { 2 } \left( { \frac { 3x } { 4 } -\frac { x^2 } { 8 } -\ln (1+x) }\right)_0^1 =-\frac { 1 } { 2 } \left( { \frac { 3 } { 4 } -\frac { 1 } { 8 } -\ln 2 }\right)=\frac { 1 } { 2 } \left( { \ln 2-\frac { 5 } { 8 } }\right)$
Пример 2
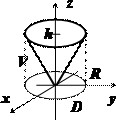
$I=\iiint\limits_V { z\cdot dxdydz } ,\;V:\left[{ \begin{array} { l } z^2=\frac { h^2 } { R^2 } \left( { x^2+y^2 }\right), \\ z=h. \\ \end{array} }\right.$ Здесь $\mathbf { \textit { V } } $ - внутренность конуса, $\mathbf { \textit { D } } $ - проекция круга, получающегося при сечении этого конуса плоскостью $\mathbf { \textit { z } } =\mathbf { \textit { h } } $ на $\mathbf { \textit { Оху } } $, т.е. круг, ограниченный кривой $h^2=\frac { h^2 } { R^2 } \left( { x^2+y^2 }\right)\Rightarrow x^2+y^2=R^2$, поэтому $I=\iint\limits_D { dxdy\int\limits_ { \frac { h } { R } \sqrt { x^2+y^2 } } ^h { zdz } = } \iint\limits_D { \left. { \frac { z^2 } { 2 } }\right|_ { \frac { h } { R } \sqrt { x^2+y^2 } } ^h dxdy= } \frac { 1 } { 2 } \iint\limits_D { \left[ { h^2-\frac { h^2 } { R^2 } \left( { x^2+y^2 }\right) }\right]dxdy } =$
$=\frac { h^2 } { 2R^2 } \iint\limits_D { \left[ { R^2-\left( { x^2+y^2 }\right) }\right]dxdy } =$ { переходим к полярным координатам } $=\frac { h^2 } { 2R^2 } \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^R { \left[ { R^2-r^2 }\right]rdr } = \frac { h^2 } { 2R^2 } \int\limits_0^ { 2\pi } { \left[ { R^2\frac { r^2 } { 2 } -\frac { r^4 } { 4 } }\right]_0^R d\varphi } =\frac { h^2 } { 2R^2 } 2\pi \frac { R^4 } { 4 } =\frac { \pi h^2R^2 } { 4 } $.
Вычислим тот же интеграл по другой формуле перехода к повторному интегралу: $I=\int\limits_0^h { dz\iint\limits_ { D_z } { zdxdy } } =\int\limits_0^h { zdz\iint\limits_ { D_z } { zdxdy } } =\int\limits_0^h { zdz\iint\limits_ { D_z } { dxdy } } =\int\limits_0^h { zdz\cdot s(D_z ) } =$ внутренний двойной интеграл - интеграл от функции, равной 1, поэтому он равен площади круга, получающегося при сечении конуса плоскостью $z=const$, уравнение ограничивающей окружности, площадь $s(D_z )=\frac { \pi z^2R^2 } { h^2 } )=\int\limits_0^h { z\frac { \pi z^2R^2 } { h^2 } dz } =\frac { \pi R^2 } { h^2 } \cdot \left. { \frac { z^4 } { 4 } }\right|_0^h =\frac { \pi h^2R^2 } { 4 } $.
Это решение оказалось проще; мы сыграли на том, что подынтегральная функция не зависит от $\mathbf { \textit { х } } $ и $\mathbf { \textit { у } } $.
Далее:
Гармонические поля
Поток жидкости через поверхность
Условия независимости криволинейного интеграла от пути интегрирования
Криволинейный интеграл первого рода
Равносильные формулы алгебры высказываний
Частные случаи векторных полей
Теорема о предполных классах
Замена переменных в тройном интеграле
Критерий полноты {формулировка}. Лемма о несамодвойственной функции
Лемма о построении множества $[F]_{x1,x2}$
Критерий полноты {формулировка}. Лемма о немонотонной функции
Теорема Стокса
Логические операции над высказываниями
Класс $T_1$. Теорема о замкнутости класса $T_1$
Введение
Огравление $\Rightarrow $
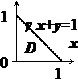
Комментарии ()