Вычисление вероятности заданного отклонения

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины $X$ от ее математического ожидания по абсолютной величине меньше заданного положительного числа $\xi $, т.е. требуется найти вероятность осуществления неравенства $\left| { X-a }\right|\prec \xi $

Заменим его равносильным $-\xi \prec X-a\prec \xi или a-\xi \prec X\prec \xi -a$.

Воспользуемся формулой Лапласа (*) $ P( { \alpha \prec X\prec \beta } )=\Phi ( { \frac { \beta -a } { \sigma } } )-\Phi ( { \frac { \alpha -a } { \sigma } } ) $ получим

$\begin{array} { l } P( { \left| { X-a }\right|\prec \xi } )=P( { a-\xi \prec X\prec \xi +a } )=\Phi ( { \frac { ( { a+\xi } )-a } { \sigma } } )-\Phi ( { \frac { a-\xi -a } { \sigma } } )= \\ =\Phi ( { \frac { \xi } { \sigma } } )-\Phi ( { \frac { -\xi } { \sigma } } )=2\Phi ( { \frac { \xi } { \sigma } } ) \\ \end{array} $

В частности для $a=0$

$P( { \left| X \right|\prec \xi } )=2\Phi ( { \frac { \xi } { \sigma } } )$

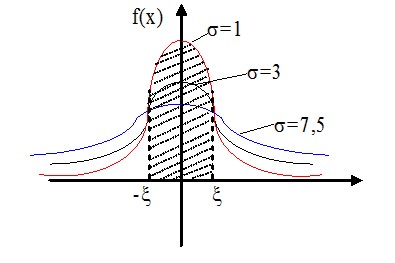
Из рисунка видно, что вероятность того, что случайная величина $X$ примет значения $\left| X \right|\prec \xi ( { при\,a=0 } )$ больше у той кривой, где $\sigma -$ меньше. Этот факт полностью соответствует вероятностному смыслу $\sigma , \sigma -$ есть среднее квадратическое отклонение, оно характеризует рассеяние случайной величины вокруг ее математического ожидания.

Замечание. Если событие $\left| { X-a }\right|\prec \xi $ осуществляется с вероятностью $P$, то противоположное событие $\left| { X-a }\right|\geqslant \xi $ с вероятностью $1-P=q$

Пример. Случайная величина $X$ распределена нормально. Математическое ожидание 20 и среднее квадратическое отклонение 10. Найти вероятность того, что отклонение от математического ожидания по абсолютной величине будет меньше 3. $ \begin{array} { l } P( { \left| { X-a }\right|\prec \xi } )=2\Phi ( { \frac { \xi } { \sigma } } ) \\ P( { \left| { X-20 }\right|<3 } )=2\Phi ( { \frac { 3 } { 10 } } )=2\Phi ( { 0,3 } )=2\cdot 0,1179=0,2358 \\ \end{array} $