Влияние параметров нормального распределения на форму кривой

Найдем влияние $a$ и $\delta $ на форму нормальной кривой $ y=\frac { 1 } { \sigma \sqrt { 2\pi } } e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } $

Известно, что графики функций $f( x )$ и $f( { x-a } )-$ имеют одинаковую форму, но сдвинуты на $a$, вправо, при $a\succ 0$ и влево при $a\prec 0$. Отсюда следует, что изменение параметра $a$ { математического ожидания } форму нормальной кривой не изменяет, а приводит лишь к ее сдвигу вдоль оси $OX$, вправо, если $a-$ возрастает и влево, если $a-$ убывает.

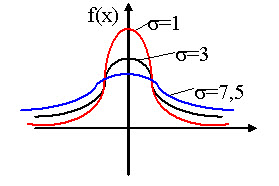
Исследуя $\sigma $, вспомним, что $max$ кривой нормального распределения находится в точке $y=\frac { 1 } { \sigma \sqrt { 2\pi } } $,

При росте $\sigma $ максимум убывает, а сама кривая становится более пологой, если $\sigma -$ убывает, то кривая растягивается вдоль оси $OY$.

Но при любых значениях $a$ и $\sigma$ площадь под кривой постоянна и равна 1. При $a=0$, $ \sigma =1-$ получаем нормированную кривую, кривую Гаусса.

Но при любых значениях $a$ и $\sigma $ площадь под кривой постоянна и равна 1.