Равномерное распределение

При решении практических задач приходится сталкиваться с различными распределениями случайной величины.

Опр. Распределение случайной величины называется равномерным если, на интервале которому принадлежат все возможные значения случайной величины, плотность распределения постоянна.

Найдем плотность равномерного распределения $f( x )$ считая, что все возможные значения случайной величины $X$ заключены на интервале $\left[ { a,b }\right]$ и $f( x )=C$.

Найдем $C$. Причем $f( x )=0$ при $x\geqslant b$ и $x\leqslant a$.

Так как все возможные значения случайной величины $X\in ( { a,b } )$ то должно выполнятся соотношение

$\int\limits_a^b { f( x )dx } =1$ или $\int\limits_a^b { Cdx } $. Тогда $Cx\left| { _a^b }\right.=1\Rightarrow C=\frac { 1 } { b-a } $

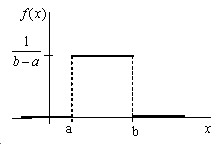
Итак: \begin{equation} \label { eq12 } f( x )=\left\{ { { \begin{array} { \c } { 0,если\,x\leqslant a } \\ { \frac { 1 } { b-a } ,если\,a<x\leqslant b } \\ { 0,если\,x>b } \\ \end{array} }}\right. \end{equation} Функция плотности равномерного распределения.

График плотности равномерного распределения

Числовые характеристики равномерного распределения

1. Математическое ожидание $M( x )=\int\limits_a^b { xf( x )dx } =\int\limits_a^b { x\cdot \frac { 1 } { b-a } dx=\frac { 1 } { b-a } \cdot \frac { x^2 } { 2 } \left| { _a^b }\right.=\frac { b+a } { 2 } } $
2. Дисперсия $D( x )=\int\limits_a^b { x^2f( x )dx-M^2( x )=\frac { ( { b-a } )^2 } { 12 } } $
3. Среднее квадратическое отклонение $\sigma ( x )=\frac { b-a } { 2\sqrt 3 } $.