Плотность распределения

Плотность распределения вероятностей непрерывной случайной величины

Опр Плотностью распределения вероятностей непрерывной случайной величины $X$ называют функцию $f( x )-$ первую производную от функции распределения $F( x )$ \begin{equation} \label { eq2 } { F } '( x )=f( x ) \end{equation}

Следовательно, функция распределения $F( x )$ является первообразной для функции плотности распределения вероятностей $f( x )$.

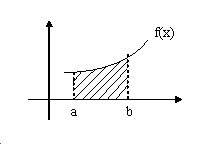
Теорема Вероятность того, что непрерывная случайная величина X примет значение принадлежащее интервалу $( { a,b } )$ равна определенному интегралу от плотности. \begin{equation} \label { eq3 } P( { a\leqslant X<b } )=\int\limits_a^b { f( x )dx } \end{equation}

Геометрически этот результат можно трактовать так: вероятность того, что случайная величина $X$ примет значение принадлежащее интервалу $( { a,b } )$ равна площади криволинейной трапеции.

Нахождение функции распределения по известной плотности распределения

Зная плотность распределения вероятностей $f( x )$ можно найти функцию распределения $F( x )$ по формуле: \begin{equation} \label { eq4 } F( x )=\int\limits_ { -\infty } ^x { f( x )dx } \end{equation}

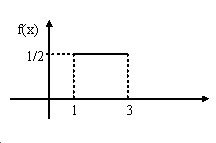
Пример. Найти функцию распределения по данной плотности и построить график. $ f( x )=\left\{ { { \begin{array} { \c } { 0,при\,x=1 } \\ { \frac { 1 } { 2 } ,при\,1<x\leqslant 3 } \\ { 0,при\,x>3 } \\ \end{array} } }\right. $

Решение. Построим график функции плотности распределения вероятностей.

$F( x )=\int\limits_ { -\infty } ^x { f( x )dx } $

Воспользуемся формулой

• при $x\leqslant 1$ из условия $f( x )=0,\Rightarrow F( x )=0 $
• при $\,1<x\leqslant 2,\, f( x )=\frac { 1 } { 2 } $, тогда

$F( x )=\int\limits_ { -\infty } ^x { f( x )dx } =\int\limits_ { -\infty } ^1 { 0dx } +\int\limits_1^x { \frac { 1 } { 2 } dx } =\frac { 1 } { 2 } x\left| { _ { _1 } ^ { ^x } }\right.=\frac { x-1 } { 2 } $

если $x>3$, тогда $ F( x )=\int\limits_ { -\infty } ^x { f( x )dx } =\int\limits_ { -\infty } ^1 { 0dx } +\int\limits_1^3 { \frac { 1 } { 2 } dx } +\int\limits_3^x { 0dx } =\frac { x } { 2 } \left| { _ { _1 } ^ { ^3 } }\right.=1. $

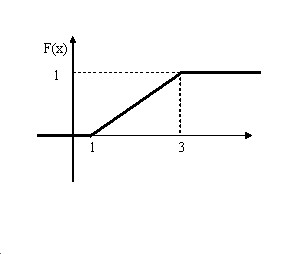
Итак $ F( x )=\left\{ { { \begin{array} { \c } { 0,если\,x\leqslant 1 } \\ { \frac { x-1 } { 2 } ,если\,1<x\leqslant 3 } \\ { 1,если\,x>3 } \\ \end{array} } }\right. $

Построим график функции распределения

Свойства плотности распределения

1). Плотность распределения неотрицательная функция $f( x )\geqslant 0$.

Доказательство Известно, что функция распределения $F( x )-$ неубывающая, следовательно, ее производная $ { F } '( x )=f( x )$ неотрицательная функция.

Геометрически это означает, что график $f( x )$ расположен выше оси OX или на оси OX.

График $f( x )$плотности распределения называется кривой распределения.

2). Несобственный интеграл от плотности распределения в пределах от $( { -\infty ,\infty } )$ равен 1. \begin{equation} \label { eq5 } \int\limits_ { -\infty } ^\infty { f( x ) } dx=1 \end{equation}

Если $X$ задана на $( { a,b } )$, то $\int\limits_a^b { f( x )dx=1 } $

Геометрически это означает, что площадь под кривой распределения равна 1.