Оценка отклонения теоретического распределения от нормального. Асимметрия и эксцесс

При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят две специальные характеристики - асимметрию и эксцесс.

Если распределение случайной величины симметрично относительно математического ожидания, то все центральные моменты нечетного порядка равны нулю.

Это объясняется тем, что в силу симметричности для каждого $+( { X-M( X ) } )$ найдется $-( { X-M( X ) } )$ с одинаковой вероятностью.

Если центральный момент нечетного порядка не равен 0, то говорят об асимметричности распределения, чем больше момент, тем больше асимметрия

Поэтому в качестве характеристики асимметрии разумнее всего взять какой-нибудь нечетный момент т.к. 1-го порядка всегда 0, то возьмем 3-го порядка.

Опр. Коэффициентом асимметрии $A$ называется величина $A=\frac { M_3 } { \sigma _x^3 } $, где $\sigma _x$ - среднее квадратическое отклонение. $M_3-$ центральный момент 3-го порядка.

Рассмотрим два случая**

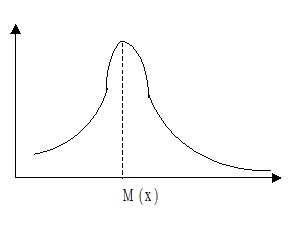
1) Если $A>0$ - это говорит о влиянии на центральный момент 3-го порядка $M_3$ отрицательных отклонений и форма кривой принимает вид: { пологая слева } кривая сама асимметрична

2) Если $A>0$ - преобладает влияние положительных отклонений и кривая полога справа.

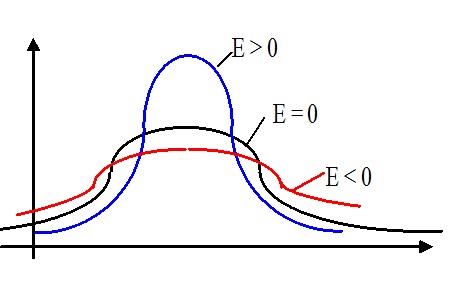
Опр Эксцессом $E$ называется величина $ E=M_4 /\sigma _x^4 -3 $

Можно показать, что для наиболее распространённого в природе нормального распределения $M_4 /\sigma _x^4 =3$ т.е. эксцесс равен 0. Если $E>0$ { эксцесс $>0$ } , то кривая более острая, если $E>0$, то более пологая.