Элементы комбинаторики в курсе теории вероятностей

Комбинаторика - один из разделов современной математики. Центральная задача комбинаторики - задача размещения объектов в соответствии со специальными правилами. Причем объекты принадлежат некоторому конечному множеству.

Под множеством будем понимать определенную совокупность объектов и обозначать заглавными буквами A, B, C.

Каждое множество определяется принадлежащими ему элементами $ { \rm A } =\left\{ { \chi _1 ,\chi _2 ,\ldots \chi _n }\right\} $.

• Запись $\chi \in { \rm A } $ означает, что $\chi $ принадлежит A.
• Запись $\chi \notin { \rm A } $ или $\chi \bar { \in } { \rm A } $ означает, что $\chi$ не принадлежит A.

Число элементов множества будем обозначать $n { A } $.

Простейшие операции над множествами:

1). Сложение или объединение обозначается знаком $\cup $

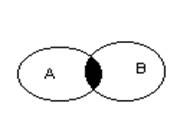
$ \chi \in { \rm A } \cup { \rm B }\Leftrightarrow \left\{ { \,\chi \in { \rm A } \,\,\vee \chi \in B }\right\} $

2). Умножение или пересечение, обозначается знаком $\cap $

$ \chi \in \left( { { \rm A } \cap { \rm B } }\right)\Leftrightarrow \left( { \chi \in { \rm A } \wedge \chi \in { \rm B } }\right) $

3). Вычитание. Обозначается знаком / и читается: А без В

$\chi \in \rm A/B\Rightarrow \left[ \chi \in A\wedge \chi \notin B\right]$

Операции над множествами

1). Правило сложения множеств

$n\left( { { \rm A } \cup { \rm B } }\right)=n\left( { \rm A }\right)\cup n\left( { \rm B }\right)$, при условии, что $ { \rm A } \cap { \rm B } =\emptyset $

2). Умножение { декартовое произведение }

$ n\left( { { \rm A } \times { \rm B } }\right)=n\left( { \rm A }\right)\cdot n\left( { \rm B }\right) $