Группировка наблюдений
Группировка наблюдений
При большом числе наблюдений, $n>80$, статистический материал, помещённый в таблицу, трудно обозрим. Поэтому составляется группировка. Это делается так: Находится
- размах выборки,
- шаг выборки,
- интервалы { разбиение на интервалы } ,
- центры интервалов,
- абсолютные частоты,
- относительные частоты.
- Чтобы найти размах выборки надо найти максимальные и минимальные значения вариант. Разность между ними называется размахом выборки $x_ { \max } -x_ { \min } =\Delta $.
- Определим шаг выборки. Для этого надо разделить $\Delta $ на $k$ - частей, где $k$ должно быть не более $20\div 25$ и не менее $6\div 10$. Обычно $6\div 10\leqslant k\leqslant 20\div 25$. Иногда $k$ считают по формуле $\log _2 n+1\approx k$, где $n$ - объём выборки. Шаг выборки вычисляется по формуле $h=\frac { \Delta } { k } $.
- Разбить на интервалы шириной $h$ по формуле $[x_i \,,\,x_i +h)$.
- Найти центры интервалов по формуле $x_i =\frac { x_i +x_ { i+1 } } { 2 } $.
- Найти абсолютные частоты. Для этого нужно подсчитать число выборочных значений $n_i $ величины $X$, попадающей в каждый интервал. Существует контроль $\sum { n_i =n } $.
- Подсчитать относительные частоты по формуле $W_i =\frac { n_i } { n } $.
- Выписать полученные интервалы или центры интервалов, выборочные значения и относительные частоты в таблицу.
- Представить выборку графически. Графическим представлением является полигон и гистограмма.
Полигон и гистограмма
Определение Полигоном абсолютных частот называют ломаную линию, отрезки которой соединяют точки $( { x_1 ,n_1 } ),( { x_2 ,n_2 } ),( { x_3 ,n_3 } )\ldots ( { x_k ,n_k } )$.
На оси абсцисс откладывают варианты $x_i $, на оси ординат - соответствующие им частоты $n_i $.
Определение Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки $( { x_1 ,w_1 } ),( { x_2 ,w_2 } ),( { x_3 ,w_3 } )\ldots ( { x_k ,w_k } )$. Для построения полигона относительных частот на оси $OX$ откладывают варианты $x_i $, а на оси ординат соответствующие им относительные частоты $w_i $. Точки $( { x_i ,w_i } )$ соединяют прямыми и получают полигон относительных частот.
Определение Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями служат интервалы длиной $h$, а высотами являются плотности частоты $\frac { n_i } { h } $. Площадь гистограммы частот равна сумме всех частот, т. е. объёму выборки.
Определение Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников с основаниями длиной $h$ и высотами $\frac { W_i } { h } $ { плотность относительных частот } . Площадь гистограммы равна сумме всех относительных частот, т. е. 1
Замечание Полигон и гистограмма строятся для того, чтобы получить представление о форме функции плотности распределения.
Пример группировки
Составить группировку и представить её графически, разбив на шесть интервалов
$\mathbf { 16\,\,\,\, } \mathbf { 17\,\,\,\, } \mathbf { 9\,\,\,\, } \mathbf { 13\,\,\,\, } \mathbf { 21\,\,\,\, } \mathbf { 11\,\,\,\, } \mathbf { 7\,\,\,\, } \mathbf { 19\,\,\,\, } \mathbf { 5\,\,\,\, } \mathbf { 20 } $
$\mathbf { 17\,\,\,\, } \mathbf { 5\,\,\,\,7\,\,\,\, } \mathbf { 18\,\,\,\, } \mathbf { 11\,\,\,\, } \mathbf { 4\,\,\,\,6\,\,\,\, } \mathbf { 22\,\,\,\,21\,\,\,\, } \mathbf { -1 } $
$\mathbf { 15\,\,\,\, } \mathbf { 22\,\,\,\, } \mathbf { 19\,\,\,\, } \mathbf { 23\,\,\,\, } \mathbf { 15 } $
Объём выборки $n=25$
1) $x_ { \max } =23,x_ { \min } =-1,\Delta =x_ { \max } -x_ { \min } =23+1=24$.
2) Разделим $\Delta $ на шесть частей $h=\frac { 24 } { 6 } =4$.
Вывод Будем иметь шесть интервалов, ширина интервала $h=4$.
3) Найдём выборочные значения $n_i $ в каждом интервале. Контроль $\sum { n_i =n } $
4) Подсчитаем относительные частоты $ W_i =\frac { n_i } { n } $
5) Подсчитаем плотность относительных частот $ f( x )=\frac { W_i } { h } . $
6) Строим полигон и гистограмму.
Занесем полученные значения в таблицу.
\begin{array} { |l|l|l|l|l|l|l| } \hline №& Интервал& Выборочные~частоты~ n_i & x_i -центр~интервала& W_i =\frac { n_i } { n } & f( x )=\frac { W_i } { h } & \frac { n_i } { h } \\ \hline 1& [ -1,3 ]& 1& 1& 0,04& 0,01& 0,25 \\ \hline 2& ( 3,7 ]& 6& 5& 0,24& 0,06& 1,5 \\ \hline 3& ( 7,11 ]& 3& 9& 0,12& 0,03& 0,75 \\ \hline 4& ( 11,15 ]& 3& 13& 0,12& 0,03& 0,75 \\ \hline 5& ( 15,19 ]& 6& 17& 0,24& 0,06& 1,5 \\ \hline 6& ( 19,23 ]& 6& 21& 0,24& 0,06& 1,5 \\ \hline \sum & & \sum { n_i =n } =25& & \sum { W_i =1 } & &\\ \hline \end{array}
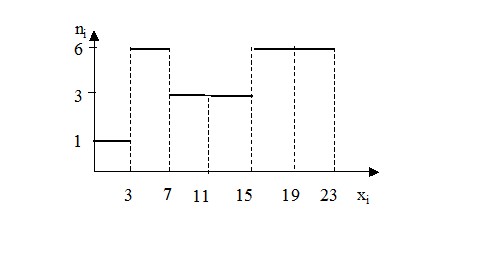
Гистограмма частот n$_ { i } $
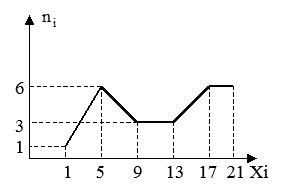
 полигон частот $n_i $ для средины интервалов
полигон частот $n_i $ для средины интервалов
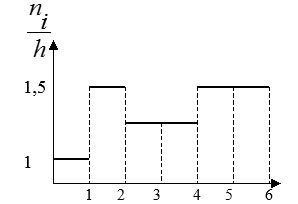
Гистограмма плотности частот $\frac { n_i } { h } $
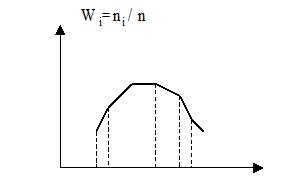
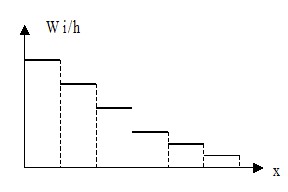
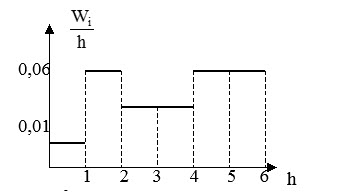
Гистограмма плотности относительных частот $\frac { W_i } { h } $
Эта величина носит вероятностный характер.
По полученной гистограмме выдвигается гипотеза о равномерном распределении.
Далее:
Вычисление двойного интеграла. Двукратный интеграл
Выражение площади плоской области через криволинейный интеграл
Гармонические поля
Критерий полноты {формулировка}. Лемма о нелинейной функции
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
Теорема Остроградского
Класс $T_0$. Теорема о замкнутости класса $T_0$
Формула Гаусса - Остроградского
Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы
Равносильные формулы алгебры высказываний
Поток жидкости через поверхность
Упрощение логических функций
Вычисление площади поверхности
Критерий полноты {формулировка}. Лемма о немонотонной функции
Поверхностный интеграл второго рода и его свойства
Огравление $\Rightarrow $
Комментарии ()