Дискретная случайная величина

Случайная величина. Закон распределения дискретной случайной величины

Опр Случайной величиной называют величину, которая в результате испытания примет одно из возможных значений, заранее неизвестное.

Например. Подбрасывается монета. Заранее не известен результат. Выпадения орла или решки - случайно. Случайные величины обозначают большими буквами Х, У:

$X( { x_1 ,x_2 ,\ldots x_n } )- значения\,x_1 \ldots x_n -$ возможные значения случайной величины.

Имеется три типа случайных величин: непрерывные, дискретные, смешанные.

Опр Дискретной { прерывной } называют случайную величину, которая принимает отдельные изолированные значения. Число случайных величин может быть конечным или бесконечным.

Опр Непрерывной - называют случайную величину, которая может принимать все значения из некоторого конечного промежутка.

Опр Законом распределения дискретной случайной величины называется соответствие между возможными значениями случайной величины и их вероятностями. Закон распределения можно задать в виде таблицы:

так как события $х_ { 1 } ,х_ { 2 } ,\ldots ,х_ { n } $ образуют полную группу то $р_ { 1 } + р_ { 2 } + \ldots + р_ { n } = 1 $

Пример. Написать закон распределения для суммы выпавших очков при подбрасывании двух игральных костей.

Пояснения к примеру: число благоприятных событий m :

$ 2) \left\{ { 1 } \right.\left. 1 \right\} -всего\,1\,, $

$ 3) \left\{ { \begin{array} { l } 2 1 \\ \,1 2 \\ \end{array} } \right\} \,-всего\,2\,, $

$4) \left\{ { \begin{array} { l } 2 2 \\ 3 1 \\ 1 3 \\ \end{array} } \right\} -всего\,3\,, $

$ 5) \left\{ { \begin{array} { l } 1 4 \\ 4 1 \\ 2 3 \\ 3 2 \\ \end{array} } \right\} -всего\,4, $

$ 6) \left\{ { \begin{array} { l } 1 5 \\ 5 1 \\ 2 4 \\ 4 2 \\ 3 3 \\ \end{array} }\right\} -всего\,5\,, $

$ 7) \left\{ { \begin{array} { l } 2 5 \\ 5 2 \\ 3 4 \\ 4 3 \\ 6 1 \\ 1 6 \\ \end{array} } \right\} -всего\,6\,, $

и так далее. Закон распределения имеет вид:

\begin{array} { |l|l|l|l|l|l|l|l|l|l|l|l| } \hline X& 2& 3& 4& 5& 6& 7& 8& 9& 10& 11& 12 \\ \hline p& \frac { 1 } { 36 } & \frac { 2 } { 36 } & \frac { 3 } { 36 } & \frac { 4 } { 36 } & \frac { 5 } { 36 } & \frac { 6 } { 36 } & \frac { 5 } { 36 } & \frac { 4 } { 36 } & \frac { 3 } { 36 } & \frac { 2 } { 36 } & \frac { 1 } { 36 } \\ \hline \end{array}

Пример 2. Охотник стреляет в цель до первого попадания, но делает 5-ть выстрелов. Вероятность попадания при одном выстреле 0,8. Построить закон распределения числа произведенных выстрелов.

Решение: Событие $A =$ { попал в цель } , тогда $\bar A =$ { промах } .

• $(\bar A ' A) =$ { попал со второго раза } ,
• $(\bar A ' \bar A ' A) =$ { попал с третьего раза } ,
• $(\bar A ' \bar A ' \bar A ' A) =$ { попал с четвертого раза } ,
• $(\bar A ' \bar A ' \bar A ' \bar A) =$ { попал с пятого раза } .

Подсчитаем вероятности этих событий.

• $P_ { 1 } (A)= p =0,8$
• $P_ { 2 } (\bar A ' A) = P(\bar A)\cdot P { A } =p\cdot q=0,8\cdot 0,2=0,16$
• $P_ { 3 } (\bar A ' \bar A ' A) = P(\bar A)^ { 2 } \cdot P { A } = p\cdot q^ { 2 } =0,8\cdot 0,2^ { 2 } =0,32$
• $P_ { 4 } (\bar A ' \bar A ' \bar A ' A) = P(\bar A)^ { 3 } \cdot P { A } = p\cdot q^ { 3 } =0,8\cdot 0,2^ { 3 } =0,0064$
• $P_ { 5 } (\bar A ' \bar A ' \bar A ' \bar A) = P(\bar A)^ { 4 } \cdot =q^ { 4 } =0,2^ { 4 } =0,0016$

Контроль:

$\Sigma p_ { i } = 0,8+0,16+0,032+0,0064+0,0016=1$

Закон распределения представим в виде таблицы:

\begin{array} { |l|l|l|l|l|l| } \hline X& 1& 2& 3& 4& 5 \\ \hline p& p& q p& q^ { 2 } p& q^ { 3 } p^ { } & q^ { 4 } \\ \hline p& 0,8& 0,16& 0,032& 0,0064& 0,0016 \\ \hline \end{array}

Функция распределения дискретной случайной величины

Функцией распределения называют функцию $F(x)$, определяющую вероятность того, что случайная величина $X$ в результате испытания примет значение, меньшее $х$, т. е. $F(x)=p(X<x)$. функция распределения д. с. в. строится по ряду распределения. Воспользуемся рядом, полученным в предыдущем примере.

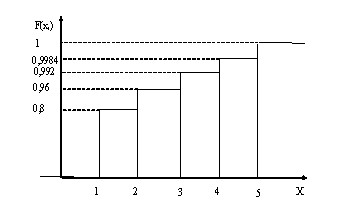
Построим график функции распределения д.с.в.

$ F(x_i )=\left\{ { \begin{array} { l } 0:x\in (-\infty , 1) \\ p_1 =0,8: x\in [\,1,\,2) \\ p_1 +p_2 =0,8+0,16=0,96: x\in [\,2,\,3) \\ p_1 +p_2 +p_3 =0,8+0,16+0,32=0,992: x\in [\,3,\,4) \\ p_1 +p_2 +p_3 +p_4 =0,8+0,16+0,32+0,064=0,9984: x\in [\,4,\,5) \\ p_1 +p_2 +p_3 +p_4 +p_5 =0,8+0,16+0,32+0,064+0,016=1, \\ \,x\in [\,5,\,\infty ] \\ \end{array} }\right. $

Функция распределения дискретной случайной величины - это ступенчатая разрывная функция.

Свойства функции распределения

1. функция распределения случайной величины есть не отрицательная функция, заключенная между нулем и единицей: $0\leqslant F(x)\leqslant 1$.
2. функция распределения случайной величины есть неубывающая функция на всей числовой оси.
3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна единице т. е. $F(-\infty )=\mathop { \lim } \limits_ { x\to -\infty } F(x)=0, F(+\infty )=\mathop { \lim } \limits_ { x\to +\infty } F(x)=1$.
4. Вероятность попадания случайной величины в интервал $[x_1 ,x_2 )$ равна приращению ее функции распределения на этом интервале, т. е. $P(x_1 \leqslant X<x_2 )=F(x_2 )-F(x_1 )$.

Биномиальное распределение

Если мы подсчитываем вероятность наступления события $k$ раз при $n$ испытаниях по формуле Бернулли $ P_n ( k )=C_n^k \cdot p^k\cdot q^ { n-k } $

Такое распределение вероятности называется биномиальным, потому что правая часть равенства совпадает с общим членом разложения бинома Ньютона. $ ( { p+q } )^n=C_n^n p^n+C_n^ { n-1 } p^ { n-1 } q+C_n^ { n-2 } p^ { n-2 } q^2+\ldots +C_n^k p^kq^ { n-k } +\ldots +C_n^0 p^0q^0 $

Пример. Монета брошена 2 раза. Написать закон распределения случайной величины $X$ - числа выпадений герба.

Решение: Вероятность появления герба $р = 1/2$, не появления $q = 1/2$. Закон распределения будет иметь вид.

\begin{array} { |l|l|l|l| } \hline X& 0& 1& 2 \\ \hline Р_ { 2 } (k)& С_ { 2 } ^ { 0 } p^ { 0 } q^ { 2 } & С_ { 2 } ^ { 1 } p^ { 1 } q^ { 1 } & С_ { 2 } ^ { 2 } p^ { 2 } q^ { 0 } \\ \hline Р & 0,25& 0,5& 0,25 \\ \hline \end{array}

Контроль: $\Sigma р_ { i } =0,25+0,5+0,25=1$

Распределение Пуассона

Пусть производится n испытаний. Вероятность появления события $A$ постоянна и равна P. Для подсчета вероятности появления события $А$ $k$ раз при $n$ испытаниях $P_n ( k )$ можно использовать формулу Бернулли или Лапласа { если $n$ большое, $n>100$ } . Но для массовых и редких явлений { когда $n$ велико, а $p$ мало $(p\leqslant 0,1)$ и $np<10$ лучше применять формулу Пуассона.

$P_n ( k )=\frac { \lambda ^k\cdot e^ { -\lambda } } { k! } $, где $\lambda =np$

$P_n ( { m\leqslant k } )=e^ { -\lambda } \sum\limits_ { m=0 } ^k { \frac { \lambda ^m } { m! } } $

Геометрическое распределение

Пусть вероятность появления события $A$ есть $p$. Не появления- $q$ и испытание заканчивается, если только событие $A$ появилось. Пусть в первых $k-1$ испытаниях событие $A$ не появилось, а в $k$ появилось. Тогда вероятность этого сложного события равна $ P( { x=k } )=q^ { k-1 } \cdot p $

Пример. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель 0,6. Найти вероятность того, что попадание произойдет при третьем выстреле.

$ P( { x=3 } )=q^2\cdot p=0,4^2\cdot 0,6=0,096 $

Гипергеометрическое распределение

Рассмотрим задачу: В партии из $N$ деталей имеется $n$ стандартных. Наудачу отбирают $m$ деталей. Найти вероятность того, что среди отобранных $m$деталей $k$ стандартных.

Решение. Общее число исходов - это есть число способов которыми можно извлечь $m$ деталей из $N$ т.е. $C_N^m $.

Число благоприятных исходов: будет сложным событием состоящим в том, что из $n$стандартных деталей $k$штук можно взять числом способов $C_n^k $, а оставшихся $m-k$ нестандартных можно взять из $N-n$ нестандартных числом способов равным $C_ { N-n } ^ { m-k } $. Тогда число благоприятных исходов есть $C_n^k \cdot C_ { N-n } ^ { m-k } $. Вероятность того, что среди отобранных $m$ деталей будет стандартных $k$ есть:

$ P( k )=\frac { C_n^k \cdot C_ { N-n } ^ { m-k } } { C_N^m } $