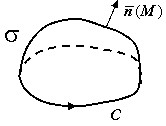
Теорема Стокса
Пусть в пространственной области $\mathbf { \textit { V } } $ задано гладкое векторное поле $\sigma \bar { a } $(M) и $\sigma $ - незамкнутая кусочно-гладкая поверхность, ограниченная контуром $\mathbf { \textit { C } } $. Единичный вектор нормали $\bar { n } (M)$ выбирается так, что с его конца направление обхода $\mathbf { \textit { C } } $ видно совершающимся против часовой стрелки. Тогда циркуляция поля $\bar { a } $ по контуру $\mathbf { \textit { C } } $ равна потоку ротора этого поля через поверхность $\sigma $: $\oint\limits_C { \bar { a } \cdot d\bar { r } } =\iint\limits_\sigma { rot~\bar { a } \cdot \bar { n } d } \sigma $.
Приведённую формулу называют формулой Стокса в векторной форме. В координатной форме формула Стокса имеет вид
$\oint\limits_C { Pdx+Qdy+Rdz } =\iint\limits_\sigma { \left( { \frac { \partial R } { \partial y } -\frac { \partial Q } { \partial z } }\right)dydz+\left( { \frac { \partial P } { \partial z } -\frac { \partial R } { \partial x } }\right)dxdz+\left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)dxdy } $ или $ \oint\limits_C { Pdx+Qdy+Rdz } =\iint\limits_\sigma { \left[ { \left( { \frac { \partial R } { \partial y } -\frac { \partial Q } { \partial z } }\right)\cos \alpha +\left( { \frac { \partial P } { \partial z } -\frac { \partial R } { \partial x } }\right)\cos \beta z+\left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)\cos \gamma }\right]d\sigma } . $ Мы примем эту формулу без доказательства.
Пример непосредственного вычисления циркуляции векторного поля и вычисления по формуле Стокса
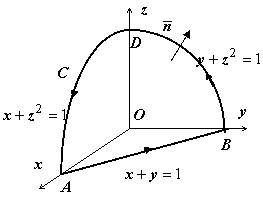
Требуется вычислить циркуляцию поля $\bar { a } =y\bar { i } -\bar { j } +xz\bar { k } $ по контуру $\mathbf { \textit { C } } $, образующемуся в результате пересечения поверхности $x+y+z^2=1$ с координатными плоскостями.
Решение. Непосредственное вычисление
$ Ц$=\oint\limits_C { \bar { a } \cdot d\bar { r } } =\oint\limits_C { ydx-dy+xzdz } =\oint\limits_ { \mathop { AB } \limits^\cup } { \bar { a } \cdot d\bar { r } } + \oint\limits_ { \mathop { BD } \limits^\cup } { \bar { a } \cdot d\bar { r } } +\oint\limits_ { \mathop { DA } \limits^\cup } { \bar { a } \cdot d\bar { r } } $
- На $\mathbf { \textit { AB } } z=dz=0,\,y=1-x,\,dy=-dx$, поэтому $ W_1 =\int\limits_ { \mathop { AB } \limits^\cup } { \bar { a } \cdot d\bar { r } } =\int\limits_1^0 { \left[ { (1-x)-(-1) }\right]dx } =\int\limits_1^0 { (2-x)dx } =-\left. { \frac { (2-x)^2 } { 2 } }\right|_1^0 = \\ =-2+1/2=-3/2. $
- На $\mathbf { \textit { BD } } x=dx=0,\,y=1-z^2,\,dy=-2zdz$, поэтому $W_2 =\int\limits_ { \mathop { BD } \limits^\cup } { \bar { a } \cdot d\bar { r } } =-\int\limits_1^0 { dy } =-\left. y \right|_1^0 =1$.
- На $\mathbf { \textit { DA } } y=dy=0,\,x=1-z^2,\,dx=-2zdz$, поэтому $W_3 =\int\limits_ { \mathop { DA } \limits^\cup } { \bar { a } \cdot d\bar { r } } =\int\limits_1^0 { (1-z^2)zdz } =\left. { \left( { \frac { z^2 } { 2 } -\frac { z^4 } { 4 } }\right) }\right|_1^0 =-\frac { 1 } { 4 } $.
Итак, Ц$=W_1 +W_2 +W_3 =-\frac { 3 } { 2 } +1-\frac { 1 } { 4 } =-\frac { 3 } { 4 } $.
Вычисление по формуле Стокса
Находим ротор поля $\bar { a } $:$rot~\bar { a } =\left| { \begin{array} { l } \,\,\bar { i } \,\,\,\bar { j } \,\,\,\bar { k } \\ \frac { \partial } { \partial x } \,\,\,\frac { \partial } { \partial y } \,\frac { \partial } { \partial z } \\ \,y\,\,-1\,\,\,xz \\ \end{array} }\right|=-z\bar { j } -\bar { k } \mathbf { . } $
Дальше требуется определить, что мы должны взять в качестве поверхности $\sigma $ { или, как часто говорят, какую поверхность натянуть на контур $\mathbf { \textit { C } } $ } . В рассматриваемом случае ответ очевиден - единственная поверхность, которая у нас есть, это цилиндрическая поверхность $x+y+z^2=1$, следы которой в координатных плоскостях и образуют контур $\mathbf { \textit { C } } $.
Однако возможны случаи, когда удачный выбор поверхности существенно упрощает вычисления. Пусть, например, контур С - окружность, образованная пересечением параболоида $z=x^2+y^2$ и конуса $z^2=x^2+y^2$. В качестве $\sigma $ можно взять и часть параболоида и часть конуса, опирающиеся на эту окружность, но лучше всего взять часть плоскости $z=1$, ограниченную этой окружностью.
Вернёмся к задаче. Находим нормаль к $\sigma : \bar { n } =\frac { \bar { i } +\bar { j } +2z\bar { k } } { \sqrt { 1+1+4z^2 } } $, знак взят с учётом того, что должно быть $\cos \gamma >0$. Теперь $rot~\bar { a } \cdot \bar { n } =(-\bar { z } j-\bar { k } )\frac { \bar { i } +\bar { j } +2z\bar { k } } { \sqrt { 2+4z^2 } } =-\frac { 3z } { \sqrt { 2+4z^2 } } $, спроецируем $\sigma $ на $\mathbf { \textit { Охz } } : d\sigma =\frac { dxdz } { \vert \cos \beta \vert } =\sqrt { 2+4z^2 } dxdz, rot~\bar { a } \cdot \bar { n } d\sigma =-\frac { 3z } { \sqrt { 2+4z^2 } } \cdot \sqrt { 2+4z^2 } dxdz=-3zdxdz$.
Вычисляем Ц$=\iint\limits_\delta { rot~\bar { a } \bar { n } d\delta } =-3\iint\limits_ { D_ { xz } } { zdz } = =-3\int\limits_0^1 { zdz\int\limits_0^ { 1-z^2 } { dx } } =-3\int\limits_0^1 { (1-z^2)zdz } =-3\left. { \left( { \frac { z^2 } { 2 } -\frac { z^4 } { 4 } }\right) }\right|_0^1 =-\frac { 3 } { 4 } $.
Самостоятельно доказать, что если $\bar { a } (\mathbf { \textit { M } } )$ - плоское поле и $\sigma $ лежит в плоскости $\mathbf { \textit { Оху } } $, то формула Стокса сводится к формуле Грина.
Инвариантное определение ротора
Пусть $M\in V$. Возьмём малую плоскую площадку $\sigma $, ограниченную контуром $\mathbf { \textit { C } } $. По теореме Стокса циркуляция по $\mathbf { \textit { C } } $ равна Ц$=\oint\limits_C { \bar { a } \cdot d\bar { r } } =\iint\limits_\sigma { rot~\bar { a } \cdot \bar { n } d } \sigma $. Считая, что $rot~\bar { a } $ мало меняется на $\sigma $ и что поверхностный интеграл равен $rot~\bar { a } (M)\cdot \bar { n } (M)\sigma =\vert rot~\bar { a } (M)\vert \cos \varphi \cdot \sigma $, получим Ц$=\vert rot~\bar { a } (M)\vert \cos \varphi \cdot \sigma $.
Будем теперь крутить площадку вокруг точки $\mathbf { \textit { M } } $, при этом циркуляция меняется вместе с $\cos \varphi $. Максимальное значение циркуляция получит при $\varphi =0$, т.е. когда направления $rot~\bar { a } (M)$ и $\bar { n } (M)$ совпадут. Следовательно, $rot~\bar { a } (M)$ указывает направление, вокруг которого циркуляция максимальна и равна Ц$_ { \mbox { max } } =\vert rot\bar { a } (M)\vert \cdot \sigma $. Модуль ротора определяется соотношением $\vert rot\bar { a } (M)\vert =\frac { \mbox { Ц } _ { \mbox { max } } } { \sigma } $.
Далее:
Класс $T_0$. Теорема о замкнутости класса $T_0$
Вычисление поверхностного интеграла второго рода
Выражение площади плоской области через криволинейный интеграл
Векторное поле
Соленоидальное векторное поле
Формула Гаусса - Остроградского
Поток векторного поля через поверхность
Теорема о полныx системаx в Pk
Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному
Лемма о построении множества $[F]_{x1,x2}$
Механические и физические приложения поверхностного интеграла первого рода
Гармонические поля
Несобственные интегралы от неограниченной функции
Функции k-значной логики. Элементарные функции. Лемма об аналоге правила де Моргана
Огравление $\Rightarrow $
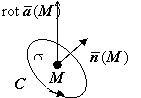
Комментарии ()