Теорема Остроградского

Пусть $\sigma $ - кусочно-гладкая замкнутая поверхность, ограничивающая область $\mathbf { \textit { V } } , \bar { а } (M)=P(M)\bar { i } +Q(M)\bar { j } +R(M)\bar { k } $ - гладкое векторное поле. Тогда поток поля $\bar { a } $ через внешнюю сторону $\sigma $ равен тройному интегралу от дивергенции поля $\bar { a } $ по $\mathbf { \textit { V } } $:

$ \iint\limits_\sigma { \bar { a } (M)\cdot \bar { n } (M)d\sigma } =\iiint\limits_V { diva\cdot dv } . $

Приведённую выше формулу обычно называют формулой Остроградского в векторной форме. Если записать её в виде $\mathop { { \iint } } \limits_\sigma { \left( { P\cdot \cos \alpha +Q\cdot \cos \beta +R\cdot \cos \gamma }\right) } d\sigma =\iiint\limits_V { \left( { \frac { \partial P } { \partial x } +\frac { \partial Q } { \partial y } +\frac { \partial R } { \partial z } }\right)dxdydz } $ или $\mathop { { \iint } } \limits_\sigma { P\cdot dydz+Q\cdot dxdz+R\cdot } dxdy=\iiint\limits_V { \left( { \frac { \partial P } { \partial x } +\frac { \partial Q } { \partial y } +\frac { \partial R } { \partial z } }\right)dxdydz } $, то получим формулу Остроградского в координатной форме. Естественно, для потока в левой части формулы могут применяться и другие обозначения.

Доказательство

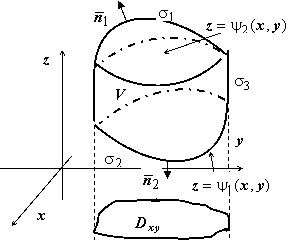
Достаточно доказать формулу в случае, когда тело $\mathbf { \textit { V } } $ - простое, т.е. проекция $\mathbf { \textit { V } } $ на любую координатную плоскость - простая область $\mathbf { \textit { D } } $, и любая прямая, перпендикулярная этой плоскости и проходящая через внутреннюю точку $\mathbf { \textit { V } } $, пересекает границу $\mathbf { \textit { V } } $ в двух точках.

Если $\mathbf { \textit { V } } $ не является простой областью, мы разобьём её на простые части, тогда сумма тройных интегралов по этим частям, в силу аддитивности, даст интеграл по всей области $\mathbf { \textit { V } } $, а при вычислении поверхностных интегралов интегралы по введённым внутренним перегородкам будут браться дважды с противоположными направлениями нормали и взаимно уничтожатся.

Кроме того, достаточно доказать формулу Остроградского для каждого из слагаемых: $\mathop { { \iint } } \limits_\sigma { P\cdot dydz } =\iiint\limits_V { \frac { \partial P } { \partial x } dxdydz } \mathbf { , } \mathop { { \iint } } \limits_\sigma { Q\cdot dxdz } =\iiint\limits_V { \frac { \partial Q } { \partial y } dxdydz } \mathbf { , } \mathop { { \iint } } \limits_\sigma { R\cdot } dxdy=\iiint\limits_V { \frac { \partial R } { \partial z } dxdydz } $, тогда сумма этих формул даст общую формулу.

Докажем, например, что $\mathop { { \iint } } \limits_\sigma { R\cdot } dxdy=\iiint\limits_V { \frac { \partial R } { \partial z } dxdydz } $.

Простую область $\mathbf { \textit { V } } $, как мы знаем, можно описать следующим образом: $V={ { (x,y,z)\vert (x,y)\in D_ { xy } ,\psi _1 (x,y)\leqslant z\leqslant \psi _2 (x,y) }}$. Вычисляем $\iiint\limits_V { \frac { \partial R } { \partial z } dxdydz } \mathbf { : } \iiint\limits_V { \frac { \partial R } { \partial z } dxdydz } =\iint\limits_ { D_ { xy } } { dxdy } \int\limits_ { \psi _1 (x,y) } ^ { \psi _2 (x,y) } { \frac { \partial R } { \partial z } dz } = -\iint\limits_ { D_ { xy } } { R(x,y,\psi _1 (x,y))dxdy } =\iint\limits_ { \sigma _1 } { R(x,y,z)dxdy } + \\ +\iint\limits_ { \sigma _2 } { R(x,y,z)dxdy } .$

Знак последнего слагаемого выбран с учётом того, что на $\sigma _2 \cos \gamma <0$. Если в полной границе области $\mathbf { \textit { V } } $ присутствует цилиндрическая составляющая $\sigma _3 $, то $\iint\limits_ { \sigma _3 } { R(x,y,z)dxdy } =0$, поэтому окончательно $\mathop { { \iint } } \limits_\sigma { R\cdot } dxdy=\iiint\limits_V { \frac { \partial R } { \partial z } dxdydz } $.

Совершенно аналогично доказываются формулы для двух других слагаемых. Формула Остроградского доказана.

Применим формулу Остроградского для решения задачи, рассмотренной в предыдущем разделе: найти поток векторного поля $\bar { a } =x\bar { i } +y^2\bar { j } +z^3\bar { k } $ через полную внешнюю поверхность тела, ограниченного поверхностями $z=-x^2-y^2,x^2+y^2+z^2=6$: $div\bar { a } =\frac { \partial x } { \partial x } +\frac { \partial y^2 } { \partial y } +\frac { \partial z^3 } { \partial z } =1+2y+3z^2$,

$\Pi =\iint\limits_\sigma { \bar { a } (M)\cdot \bar { n } (M)d\sigma } =\iiint\limits_V { div\bar { a } \cdot dv } =\iiint\limits_V { (1+2r\sin \varphi +3z^2)rdrd\varphi dz } =\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { \sqrt 2 } { \left. { \left( { z+z^3 }\right) }\right|_ { -\sqrt { 6-r^2 } } ^ { -r^2 } rdr } } + \\ +2\int\limits_0^ { 2\pi } \sin \varphi d\varphi \int\limits_0^ { \sqrt 2 } { r^2dr\int\limits_ { -\sqrt { 6-r^2 } } ^ { -r^2 } { dz } } =2\pi \int\limits_0^ { \sqrt 2 } { \left( { \sqrt { 6-r^2 } -r^2+\left( { 6-r^2 }\right)^ { 3/2 } -r^6 }\right)rdr } = \\ =2\pi \left[ \frac { 1 } { 3 } \left( { 6-r^2 }\right)^ { 3/2 } -\frac { r^4 } { 4 }\right. \left. { -\frac { 1 } { 5 } \left( { 6-r^2 }\right)^ { 5/2 } -\frac { r^8 } { 8 } }\right]_0^ { \sqrt 2 } = \\ = 2\pi \left[ { -\frac { 1 } { 3 } \left( { 8-6\sqrt 6 }\right)-1-\frac { 1 } { 5 } \left( { 32-36\sqrt 6 }\right)-2 }\right]=\frac { \pi } { 5 } \left( { 92\sqrt 6 -\frac { 362 } { 3 } }\right)$

Естественно, ответ получился тот же, но этот способ вычисления оказался самым простым.