Свойства потока векторного поля

Согласно определению, поток - поверхностный интеграл, поэтому он имеет все свойства поверхностного интеграла. Понятно, что некоторые из этих свойств теряют смысл { интеграл от единичной функции, например } , поэтому перечислим основные свойства потока.

1. Линейность. $\iint\limits_\sigma { \left( { \alpha \bar { a } _1 +\beta \bar { a } _2 }\right)\bar { n } d\sigma } =\alpha \iint\limits_\sigma { \bar { a } _1 \bar { n } d\sigma } +\beta \iint\limits_\sigma { \bar { a } _2 \bar { n } d\sigma } $;
2. Аддитивность. $\iint\limits_ { \sigma _1 \cup \sigma _2 } { \bar { a } (M)\bar { n } (M)d\sigma } =\iint\limits_ { \sigma _1 } { \bar { a } (M)\bar { n } (M)d\sigma } +\iint\limits_ { \sigma _2 } { \bar { a } (M)\bar { n } (M)d\sigma } $. Здесь $\sigma _1 $ и $\sigma _2 $ - кусочно-гладкие поверхности, которые могут пересекаться только по границам; нормали на этих поверхностях должны быть согласованы так, чтобы определять одну сторону всей составной поверхности $\sigma _1 \cup \sigma _2 $.
3. Поток меняет знак при изменении стороны поверхности { так как в каждой точке $M\in \sigma $ вектор $\bar { n } (M)$ меняется на -$\bar { n } (M))$.

Вычисление потока векторного поля

В соответствии с определением $\prod =\iint\limits_\sigma { \bar { a } (M)\bar { n } (M)d\sigma } =\iint\limits_\sigma { P(M)dydz+Q(M)dxdz+R(M)dxdy } $, поток может вычисляться и с помощью поверхностного интеграла первого рода, и с помощью поверхностного интеграла второго рода. В примере раздела Вычисление поверхностного интеграла второго рода было приведено вычисление потока поля $\bar { v } (M)=3x\bar { i } +z\bar { j } +5y\bar { k } $ через часть плоскости $2x+3y-4z=12$, ограниченную координатными плоскостями, в том и другом представлении. Рассмотрим более сложный пример.

Пример 1

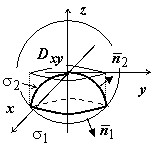
Найти поток векторного поля $\bar { a } =x\bar { i } +y^2\bar { j } +z^3\bar { k } $ через полную внешнюю поверхность тела, ограниченного поверхностями $z=-x^2-y^2,x^2+y^2+z^2=6$.

Решение. Поверхность состоит из двух частей: $\sigma _2 $ - часть поверхности параболоида $z=-x^2-y^2,$ накрытая шапочкой $\sigma _1 $ - частью нижней полусферы $z=-\sqrt { 6-x^2-y^2 } $; уровень пересечения этих поверхностей по оси $\mathbf { \textit { Oz } } $ определяется уравнением $z^2 - z = 6 $, откуда $z=-2$; проекция линии пересечения на плоскость $\mathbf { \textit { Oxy } } $ - окружность радиуса $R=\sqrt 2 $.

Выпишем нормали: $\bar { n } _1 =\pm \frac { 2x\bar { i } +2y\bar { j } +2z\bar { k } } { \sqrt { 4x^2+4y^2+4z^2 } } $; выбираем знак "+", так как на $\sigma _1 $ нормаль образует тупой угол с осью $\mathbf { \textit { Oz } } $, и коэффициент при $\bar { k } $ должен быть отрицателен { мы находимся в полупространстве $z<0$ } . С учётом того, что на $\sigma _1 x^2+y^2+z^2=6, \bar { n } _1 =\frac { x\bar { i } +y\bar { j } +z\bar { k } } { \sqrt 6 } , \vert \cos \gamma \vert =\left| { \frac { z } { \sqrt 6 } }\right|=-\frac { z } { \sqrt 6 } $. Уравнение $\sigma _2 $ в виде поверхности уровня: $x^2+y^2+z=0, \bar { n } _2 =\frac { 2x\bar { i } +2y\bar { j } +\bar { k } } { \sqrt { 4x^2+4y^2+1 } } $, знак "+", так как угол между $\bar { n } _2 $ и осью $\mathbf { \textit { Oz } } $ острый, $\vert \cos \gamma \vert =\frac { 1 } { \sqrt { 4x^2+4y^2+1 } } $.

1). Вычисление с помощью поверхностного интеграла первого рода: $\prod=\prod_ { 1 } +\prod_ { 2 } $,

$\prod_ { 1 } =\iint\limits_ { \sigma _1 } { \bar { a } (M)\bar { n } (M)d\sigma } , \prod_ { 2 } =\iint\limits_ { \sigma _2 } { \bar { a } (M)\bar { n } (M)d\sigma } $, обе поверхности однозначно проектируются на плоскость $\mathbf { \textit { Oxy } } $ в круг радиуса $R=\sqrt 2 $, поэтому $\prod_ { 1 } =\iint\limits_ { \sigma _1 } { \bar { a } (M)\bar { n } (M)d\sigma } =\iint\limits_ { D_ { xy } } { \frac { x^2+y^3+z^4 } { \sqrt 6 } \cdot \left. { \frac { -\sqrt 6 } { z } }\right|_ { z=-\sqrt { 6-x^2-y^2 } } dxdy } =\int\limits_0^ { 2\pi } { \cos ^2\varphi d\varphi \int\limits_0^ { \sqrt 2 } { \frac { r^2 } { \sqrt { 6-r^2 } } } } rdr+ \\ +\int\limits_0^ { 2\pi } { \sin ^3\varphi d\varphi \int\limits_0^ { \sqrt 2 } { \frac { r^3 } { \sqrt { 6-r^2 } } } } rdr+\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { \sqrt 2 } { \sqrt { (6-r^2)^3 } } } rdr=\frac { \pi } { 2 } \int\limits_0^ { \sqrt 2 } { \frac { (6-r^2)-6 } { \sqrt { 6-r^2 } } d(6-r^2) } -\pi \frac { 2 } { 5 } \left. { \left( { 6-r^2 }\right)^ { 5/2 } }\right|_0^ { \sqrt 2 } = \\ =\frac { \pi } { 5 } \left( { 92\sqrt 6 -\frac { 332 } { 3 } }\right)$.

$\prod_ { 2 } =\iint\limits_ { \sigma _2 } { \bar { a } (M)\bar { n } (M)d\sigma } =\iint\limits_ { D_ { xy } } { \frac { 2x^2+2y^3+z^3 } { \sqrt { 1+4(x^2+y^2) } } \cdot \left. { \sqrt { 1+4(x^2+y^2) } }\right|_ { z=-x^2-y^2 } d\sigma } = \\ =2\int\limits_0^ { 2\pi } { \cos ^2\varphi d\varphi \int\limits_0^ { \sqrt 2 } { r^2 } } rdr+2\int\limits_0^ { 2\pi } { \sin ^3\varphi d\varphi \int\limits_0^ { \sqrt 2 } { r^2 } } rdr-\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { \sqrt 2 } { r^6 } } rdr=2\pi \left. { \frac { r^4 } { 4 } }\right|_0^ { \sqrt 2 } -2\pi \left. { \frac { r^8 } { 8 } }\right|_0^ { \sqrt 2 } =-2\pi$

$\prod=\prod_ { 1 } $+$\prod_ { 2 } =\frac { \pi } { 5 } \left( { 92\sqrt 6 -\frac { 332 } { 3 } }\right)-2\pi =\frac { \pi } { 5 } \left( { 92\sqrt 6 -\frac { 362 } { 3 } }\right)_ { . } $

2). Посмотрим, к каким вычислениям приводит применение поверхностного интеграла второго рода.

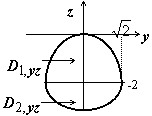
$\Pi =\iint\limits_\sigma { xdydz+y^2dxdz+z^3dxdy } $. Для вычисления $I_1 =\iint\limits_\sigma { xdydz } $ придется разбить полную поверхность $\sigma =\sigma _1 \cup \sigma _2 $ на части $\sigma _3 $, находящуюся в полупространстве $x\geqslant 0$, где $\cos \alpha \geqslant 0$, и $\sigma _4 $, находящуюся в полупространстве $x<0$, где $\cos \alpha <0$; $I_1 =\iint\limits_ { \sigma _3 } { xdydz } -\iint\limits_ { \sigma _4 } { xdydz } =2\iint\limits_ { \sigma _3 } { xdydz } $

С учётом того, что подынтегральная функция меняет знак при переходе от $\sigma _3 $ к $\sigma _4$

$ = 2\iint\limits_ { D_ { 1,yz } } { \left. x \right|_ { x=\sqrt { -y^2-z } } dydz } +2\iint\limits_ { D_ { 2,yz } } { \left. x \right|_ { x=\sqrt { 6-y^2-z^2 } } dydz } =2\int\limits_ { -\sqrt 2 } ^ { \sqrt 2 } { dy\int\limits_ { -2 } ^ { -y^2 } { \sqrt { -y^2-z } dz } +2\int\limits_ { -\sqrt 6 } ^ { -2 } { dz\int\limits_ { -\sqrt { 6-z^2 } } ^ { \sqrt { 6-z^2 } } { \sqrt { 6-y^2-z^2 } dy } } } = \\ =-4\int\limits_0^ { \sqrt 2 } { \frac { 2 } { 3 } \left. { \left( { -y^2-z }\right)^ { 3/2 } }\right|_ { -2 } ^ { -y^2 } dy+4\int\limits_ { -\sqrt 6 } ^ { -2 } { dz\cdot \frac { 1 } { 2 } \left. { \left[ { y\sqrt { 6-y^2-z^2 } +\left( { 6-z^2 }\right)\arcsin \frac { y } { \sqrt { 6-z^2 } } }\right] }\right|_0^ { \sqrt { 6-z^2 } } } } = \\ =\frac { 8 } { 3 } \int\limits_0^ { \sqrt 2 } { \left( { 2-y^2 }\right)^ { 3/2 } dy+2\int\limits_ { -\sqrt 6 } ^ { -2 } { \left( { 6-z^2 }\right)\frac { \pi } { 2 } dz } } =\frac { 8 } { 3 } \int\limits_0^ { \pi /2 } { 4\cos ^4tdt } +\pi \left. { \left( { 6z-z^3/3 }\right) }\right|_ { -\sqrt 6 } ^ { -2 } = 2\pi +\pi \left( { 4\sqrt 6 -28/3 }\right)= \\ =\pi \left( { 4\sqrt 6 -22/3 }\right)$.

Интеграл $I_2 =\iint\limits_\sigma { y^2dxdz } $ равен нулю, так как подынтегральная функция чётна по $\mathbf { \textit { у } } $, а интегралы по частям поверхности, находящихся в полупространствах $y\geqslant 0$, где $\cos \beta \geqslant 0$, и $y<0$, где $\cos \beta <0$, берутся с разными знаками.

Интеграл $I_3 =\iint\limits_\sigma { z^3dxdy } =\iint\limits_ { \sigma _2 } { z^3dxdy } +\iint\limits_ { \sigma _1 } { z^3dxdy } =$ { в соответствии со знаками } $\cos \gamma $ на $\sigma _1 $ и $\sigma _2 =\iint\limits_ { D_ { xy } } { (-x^2-y^2)^3dxdy } -\iint\limits_ { D_ { xy } } { \left( { -\sqrt { 6-x^2-y^2 } }\right)^3dxdy } =-\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { \sqrt 2 } { r^7dr } } +\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { \sqrt 2 } { \left( { 6-r^2 }\right)^ { 3/2 } rdr } } = \\ =-4\pi -\frac { 2\pi } { 5 } \left( { 32-36\sqrt 6 }\right)=\frac { 2\pi } { 5 } \left( { 36\sqrt 6 -42 }\right)$.

Поток $\Pi =\pi \left( { 4\sqrt 6 -22/3 }\right)+\frac { 2\pi } { 5 } \left( { 36\sqrt 6 -42 }\right)=\frac { \pi } { 5 } \left( { 92\sqrt 6 -\frac { 362 } { 3 } }\right)$.

Ответы, как и должно быть, совпали, однако вычисления с помощью криволинейного интеграла первого рода оказались существенно более простыми.