Нахождение потенциала

В предыдущем разделе мы доказали, что если выполняются условия потенциальности поля $\bar { a } (\mathbf { \textit { M } } )$, то $\varphi (M)=\int\limits_ { \mathop { M_0 M } \limits^\cup } { \bar { a } d\bar { r } } $, где $M_0 \in V$ - фиксированная точка. Обычно, если в точке $\mathbf { \textit { O } } (0,0,0)$ поле не имеет особенностей, то в качестве точки $M_0 (x_0 ,y_0 ,z_0 )$ берётся именно эта точка, если в этой точке поле не определено, берётся другая точка.

Интегрирование ведут по пути, состоящим из отрезков, параллельных координатным осям. В результате получим $\varphi (M)=\int\limits_ { x_0 } ^x { P(x,y_0 ,z_0 )dx } +\int\limits_ { y_0 } ^y { Q(x,y,z_0 )dy } +\int\limits_ { z_0 } ^z { R(x,y,z)dz } $.

Пример 1

Доказать, что поле $\bar { a } (x,y,z)=\frac { y\cos (xy) } { z } \bar { i } +\frac { x\cos (xy) } { z } \bar { j } -\frac { \sin (xy) } { z^2 } \bar { k } $ потенциально и найти потенциал этого поля.

Решение

Мы будем доказывать, что это поле потенциально в любой односвязной области $\mathbf { \textit { V } } $, не содержащей точку $\mathbf { \textit { O } } (0,0,0)$. Условие безвихревости поля $\bar { a } $:

$rot\bar { a } (M)=\left| { \begin{array} { l } \,\bar { i } \,\,\,\,\bar { j } \,\,\,\bar { k } \\ \frac { \partial } { \partial x } \,\,\frac { \partial } { \partial y } \,\,\frac { \partial } { \partial z } \\ \,P\,\,Q\,\,\,R \\ \end{array} }\right|=\left( { \frac { \partial R } { \partial y } -\frac { \partial Q } { \partial z } }\right)\bar { i } +\left( { \frac { \partial P } { \partial z } -\frac { \partial R } { \partial x } }\right)\bar { j } +\left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)\bar { k } =0$ в координатной форме сводится к равенствам $\frac { \partial R } { \partial y } =\frac { \partial Q } { \partial z } , \frac { \partial P } { \partial z } =\frac { \partial R } { \partial x } , \frac { \partial Q } { \partial x } =\frac { \partial P } { \partial y } $.

В нашем поле $P(x,y,z)=\frac { y\cos (xy) } { z } , Q(x,y,z)=\frac { x\cos (xy) } { z } ,R(x,y,z)=-\frac { \sin (xy) } { z^2 } $. Находим производные:

$\frac { \partial R } { \partial y } =-\frac { x\cos (xy) } { z^2 } $,

$\frac { \partial Q } { \partial z } =-\frac { x\cos (xy) } { z^2 } =\frac { \partial R } { \partial y } $,

$\frac { \partial P } { \partial z } =-\frac { y\cos (xy) } { z^2 } $,

$\frac { \partial R } { \partial x } =-\frac { y\cos (xy) } { z^2 } =\frac { \partial P } { \partial z } $,

$\frac { \partial Q } { \partial x } =\frac { \cos (xy)-xy\sin (xy) } { z } $,

$\frac { \partial P } { \partial y } =\frac { \cos (xy)-xy\sin (xy) } { z } =\frac { \partial Q } { \partial x } $ Потенциальность поля доказана.

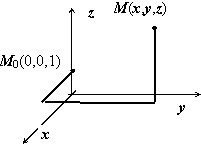
Ищем потенциал. Интеграл $\varphi (M)=\int\limits_ { \mathop { M_0 M } \limits^\cup } { \bar { a } d\bar { r } } $ вычисляем по изображённому на рисунке пути, отправляясь от точки $\mathbf { \textit { M } } _ { 0 } $(0,0,1). $\varphi (x,y,z)=\int\limits_0^x { \frac { 0\cdot \cos (x\cdot 0) } { 1 } dx } +\int\limits_0^y { \frac { x\cdot \cos (xy) } { 1 } dy } -\int\limits_1^z { \frac { \sin (xy) } { z^2 } dz } = =\left. { \sin (xy) }\right|_0^y +\left. { \frac { \sin (xy) } { z } }\right|_1^z =\sin (xy)+\left[ { \frac { \sin (xy) } { z } -\sin (xy) }\right]=\frac { \sin (xy) } { z } $.

Если бы мы взяли в качестве точки $\mathbf { \textit { M } } _ { 0 } $ другую точку $\mathbf { \textit { M } } _ { 1 } $, то получили бы выражение, отличающееся на некоторую постоянную { более точно, на $C=\int\limits_ { \mathop { M_0 M_1 } \limits^\cup } { \bar { a } d\bar { r } } )$, поэтому $\varphi (x,y,z)= \frac { \sin (xy) } { z } +C$.