Линейный интеграл и циркуляция векторного поля

Определение линейного интеграла

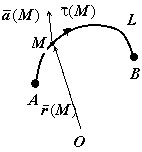
Пусть в пространственной области $\mathbf { \textit { V } } $ определено непрерывное векторное поле $\bar { a } (\mathbf { \textit { M } } ), \mathbf { \textit { L } } $ - гладкая кривая, расположенная в $\mathbf { \textit { V } } $. Линейным интегралом поля $\bar { a } $ вдоль линии $\mathbf { \textit { L } } $ называется криволинейный интеграл по длине дуги от скалярного произведения $\bar { a } (\mathbf { \textit { M } } )$ на единичный касательный вектор $\bar { \tau } (\mathbf { \textit { M } } ): W=\int\limits_L { \bar { a } (M)\cdot \bar { \tau } (M)\,ds } $.

Как и поток, этот интеграл может представляться различным образом. Так, если учесть, что произведение $\bar { \tau } (M)$ на $ds$ даёт изменение радиуса-вектора точки $\mathbf { \textit { M } } $, т.е. $\bar { \tau } \cdot ds=d\bar { r } =dx\bar { i } +dy\bar { j } +dz\bar { k } $,то $W=\int\limits_L { \bar { a } (M)d\bar { r } } $ и $W=\int\limits_L { Pdx+Qdy+Rdz } $. Следовательно, линейный интеграл может быть выражен и через линейный интеграл по координатам.

Физический смысл линейного интеграла:

если $\bar { a } (\mathbf { \textit { M } } )$ - силовое поле, то $W$ равен работе этого поля при перемещении материальной точки вдоль линии $\mathbf { \textit { L } } $ см. раздел Тройные интегралы.

Основные свойства линейного интеграла.

1). Линейность

$\int\limits_L { \left( { С_1 \bar { a } _1 +С_2 \bar { a } _2 }\right)\bar { \tau } \,ds } =С_1 \int\limits_L { \bar { a } _1 \bar { \tau } \,ds } +С_2 \int\limits_L { \bar { a } _2 \bar { \tau } \,ds } $,

2). Аддитивность

$\int\limits_ { L_1 \cup L_2 } { \bar { a } \cdot \bar { \tau } \,ds } =\int\limits_ { L_1 } { \bar { a } \cdot \bar { \tau } \,ds } +\int\limits_ { L_2 } { \bar { a } \cdot \bar { \tau } \,ds } $. Направление на каждой из частей $\mathbf { \textit { L } } _ { 1 } $ и $\mathbf { \textit { L } } _ { 2 } $ должно быть таким же, как и на всей кривой $L_1 \cup L_2 $,

3). При изменении направления вдоль $\mathbf { \textit { L } } $ линейный интеграл меняет знак.

Это следует из того, что вектор $\bar { \tau } (\mathbf { \textit { M } } )$ меняется на - $\bar { \tau } (\mathbf { \textit { M } } )$.

4). Если $\mathbf { \textit { L } } $ - векторная линия поля и движение происходит в направлении поля, то $\mathbf { \textit { W } } >0$. В этом случае вектор $\bar { \tau } (\mathbf { \textit { M } } )$ коллинеарен $\bar { a } (\mathbf { \textit { M } } )$, поэтому $\bar { a } \cdot \bar { \tau } =\mathop { \mbox { пр } \bar { a } } \limits_ { \bar { \tau } } =\vert \bar { a } \vert >0$.

Вычисление линейного интеграла

Как и любой криволинейный интеграл, линейный интеграл вычисляется сведением к определённому интегралу по параметру на кривой, обычно вычисляют криволинейный интеграл $W=\int\limits_L { Pdx+Qdy+Rdz } $. Если кривая при параметрическом задании имеет вид $L:\left\ { { \begin{array} { l } x=x(t), \\ y=y(t), \\ z=z(t), \\ \end{array} }\right. t_0 \leqslant t\leqslant t_k $, где $x(t),\,y(t),\,z(t)$- непрерывно дифференцируемые функции, то $W=\int\limits_L { P(x,y,z)\cdot dx+Q(x,y,z)\cdot dt+R(x,y,z)\cdot dz } = \\ =\int\limits_ { t_0 } ^ { t_k } { \left[ { P(x(t),y(t),z(t))\cdot { x } '(t)+Q(x(t),y(t),z(t))\cdot { y } '(t)+R(x(t),y(t),z(t))\cdot { z } '(t) }\right]dt } .$

Направление интегрирования определяется направлением движения по кривой.

Циркуляция векторного поля

Циркуляцией называется линейный интеграл векторного поля по замкнутой кривой $\mathbf { \textit { C } } $: Ц$=\oint\limits_C { \bar { a } \cdot d\bar { r } } $.

Обычно говорят, что циркуляция характеризует вращательную способность поля. Имеется в виду следующее. Если векторные линии поля замкнуты, то, как мы видели, циркуляция по ним в направлении поля положительна, при этом в гидродинамической интерпретации частицы жидкости крутятся по этим замкнутым линиям. Пусть теперь линии тока произвольны, вообразим в объёме $\mathbf { \textit { V } } $ замкнутый контур $\mathbf { \textit { C } } $. Если в результате движения жидкости этот контур будет вращаться, то поле обладает вращательной способностью, абсолютная величина циркуляции будет определять угловую скорость вращения { чем больше $\vert$ Ц $\vert $, тем выше скорость } , знак циркуляции покажет, совпадает ли направление вращения с направлением интегрирования.