Расчет сварного соединения с угловыми швами на одновременное действие продольной и поперечной сил

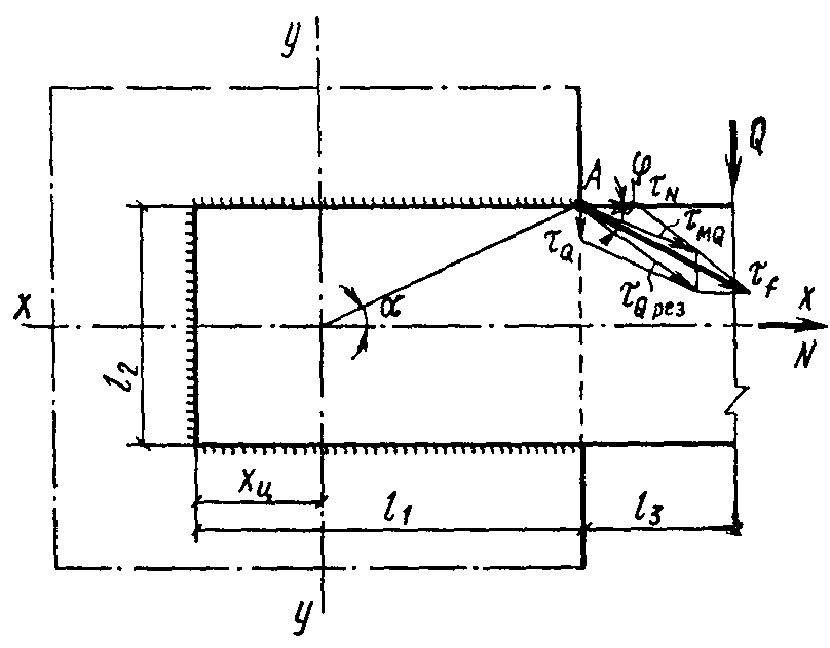
Полоса прикрепляется двумя горизонтальными и одним вертикальным швом { рис. 1 } . Продольная сила $N = 100$ кН, поперечная сила $Q = 38$ кН. Материал пластины - сталь марки ВСт3 $R_ { un } = 370$ МПа. Сварка выполняется покрытыми электродами типа Э46 $R_ { wf } = 200$ МПа, $\beta_ { f } = 0,7$. Коэффициенты условий работы $\gamma _ { wf } =\gamma _ { c } = 1$.

Необходимо определить катет углового шва.

Решение

Для указанного сочетания стали, электродов и способа сварки расчетным сечением является сечение по металлу шва. Поэтому расчет должен выполняться по формуле: $\tau _ { f } \leqslant R_ { wf } \gamma _ { wf } \gamma _ { c } $.

Принимаем $k_ { f } = 10$ мм.

1). Определяем напряжение в соединении от продольной силы $N\tau _ { N } =N / A_ { w } $, где расчетная площадь шва $A_ { w } = (2l_ { 1 } +l_ { 2 } ) k_ { f } \beta _ { f } $.

Рис. 1. К расчету сварного соединения с угловыми швами на одновременное действие продольной и поперечной сил $l_ { 1 } = 30$ см; $l_ { 2 } = 20$ см; $l_ { 3 } = 81$ см

С учетом того, что расчетная длина шва принимается меньше его полной длины на 10 мм:

$A_ { w } = (2 \cdot 29 + 20) 1 \cdot 0,7 = 54,6 см^ { 2 } $,

$\tau _ { N } = 100 \cdot 10 / 54,6 = 18,3$ МПа.

2). Определяем напряжение в соединении от поперечной силы $Q$.

Результирующее напряжение $\tau _ { Q рез } $ является суммой векторов напряжения от силы $Q$, перенесенной в центр тяжести периметра швов $\tau _ { Q } $ и напряжения от момента $\tau _ { мQ } $:

$\tau _ { Q } =Q / A_ { w } = 38 \cdot 10 / 54,6 = 7$ МПа;

$ \tau _ { мQ } =M/(I_ { fx } +I_ { fy } ^ )\sqrt { x^2+y^2 } $

Центр тяжести периметра швов определяется по формуле

$x_ { \mbox { ц } } = (l^ { 2 } _ { 1 } - 0,5l_ { 2 } k_ { f } ) / (2l_ { 1 } +l_ { 2 } ) = (900 - 0,5 \cdot 20 \cdot 1) / (60 + 20) = 11$ см.

Координаты точки $А$, наиболее удаленной от центра тяжести расчетного сечения швов: $x = 19$ см, $у = 10$ см.

Моменты инерции расчетного сечения соединения по металлу шва относительно его главных осей:

$I_ { fx } \approx \beta _ { f } { \ { } l^ { 3 } _ { 2 } k_ { f } / 12 + 2l_ { 1 } k_ { f } [(l_ { 2 } +k_ { f } ) / 2]^ { 2 } { \ } } = \\ = 0,7 { \ { } 20^ { 3 } \cdot 1/12 + 2 \cdot 29 \cdot 1[(20 + 1) / 2]^ { 2 } { \ } } = 4942$ см$^ { 4 } $,

$I_ { fy } \approx \beta _ { f } { \ { } 2 [l^ { 3 } _ { 1 } k_ { f } / 12 + l_ { 1 } k_ { f } (l_ { 1 } / 2 - x_ { \mbox { ц } } )^ { 2 } ] + l_ { 2 } k_ { f } (x_ { \mbox { ц } } +k_ { f } / 2)^ { 2 } { \ } } = \\ = 0,7 { \ { } 2 [29^ { 3 } \cdot 1/12 + 29 \cdot 1 (29 / 2 - 11)^ { 2 } ] + 20 \cdot 1 (11 + 1 / 2)^ { 2 } { \ } } = 5194$ см$^ { 4 } $.

Расстояние точки шва, наиболее удаленной от центра тяжести расчетного сечения соединения:

$\sqrt { x^2+y^2 } =\sqrt { 19^2+10^2 } =21,5$ см.

$\tau _ { мQ } = 38 \cdot 1 \cdot 10^ { 3 } / (4942 + 5194) 21,5 = 80,6$ МПа.

Результирующее напряжение от действия поперечной силы $Q$:

$\tau _ { Q { рез } } =\sqrt { \tau _ { Q } ^2 +\tau _ { мQ } ^2 +2\tau _ { Q } \tau _ { мQ } \cos \alpha } $ ,

где $\alpha $ - угол, определяемый размерами соединения { см. рис. 1);

$\tau _ { Q { рез } } =\sqrt { 7^2 +80,6^2 +2\cdot 7\cdot 80,6\cdot 0,89 } =86,9$ МПа.

3). Определяем угол между векторами $\vec { \tau } _N $ и $\vec { \tau } _ { Q { рез } } $.

Угол $\phi $ определяют, пользуясь координатным методом на плоскости и свойством скалярного произведения двух векторов: $ \cos \varphi =\vec { a } \vec { b } /\left( { \left| { \vec { a } }\right|\cdot \left| { \vec { b } }\right| }\right), $ где $\vec { a } $ и $\vec { b } $ - векторы; $\vert \vec { a } \vert $ и $\vert \vec { b } \vert $ - длины векторов.

Поскольку скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов $\vec { a } \cdot \vec { b } =x_ { 1 } x_ { 2 } +y_ { 1 } y_ { 2 } $ и длина вектора равна $ \left| { \vec { a } }\right|=\sqrt { x_1^2 +y_1^2 } ; \left| { \vec { b } }\right|=\sqrt { x_2^2 +y_2^2 } , \cos \varphi =\left( { x_1 x_2 +y_1 y_2 }\right)/\left( { \sqrt { x_1^2 +y_1^2 } \sqrt { x_2^2 +y_2^2 } }\right). $

В рассматриваемом примере координаты вектора $\vec { \tau } _N : х_ { 1 } = \tau _ { N } , y_ { 1 } = 0$; координаты вектора $\vec { \tau } _ { Q { рез } } : x_ { 2 } =\tau _ { yQ } sin \alpha , y_ { 2 } =\tau _ { yQ } cos \alpha +\tau _ { Q } $:

$\cos \varphi =\tau _ { мQ } \sin \alpha /\sqrt { (\tau _ { мQ } \sin \alpha )^2+(\tau _ { мQ } \cos \alpha +\tau _Q )^2 } = 80,6\cdot 0,46/\sqrt { (80,6\cdot 0,46)^2+(80,6\cdot 0,89+7,3)^2 } =0,43$

4). Определяем суммарное напряжение в соединении

$\tau _f =\sqrt { \tau _N^2 +\tau _ { Q { рез } } ^2 +2\tau _N \tau _ { Q { рез } } \cos \varphi } = \sqrt { 18,3^2+86,9^2+2\cdot 18,3\cdot 86,9\cdot 0,43 } =96,2$ МПа

$\tau _ { f } / R_ { wf } = 96,2 / 200 = 0,48$.

Таким образом, при $k_ { f } = 10$ мм суммарное напряжение в 0,48 раза меньше расчетного сопротивления. Следовательно, катет шва в соединении следует принять $k_ { f } = 5$ мм.

$l_ { 1 } = 20$ см; $l_ { 2 } = 16$ см; $l_ { 3 } = 90$ см

Проверка прочности соединения при $k_ { f } = 5$ мм показывает правильность расчета:

$А_ { w } = 27,3 см^ { 2 } ; \tau _ { N } = 100 \cdot 10 / 27,3 = 36,6$ МПа;

$\tau _ { Q } = 38 \cdot 10 / 27,3 = 13,9 МПа; I_ { fx } = 2366 см^ { 4 } ; I_ { fy } = 2557$ см$^ { 4 } $;

$\tau _ { мQ } = 38 \cdot 10^ { 3 } \cdot 21,5 / 4923 = 166$ МПа;

$\tau _ { Q { рез } } =\sqrt { 13,9^2 +166^2 +2\cdot 13,9\cdot 166\cdot 0,89 } =179$ МПа; $cos \phi = 0,43$;

$\tau _f =\sqrt { 36,6^2+179^2+2\cdot 36,6\cdot 179\cdot 0,43 } =198 МПа < 200$ МПа.