Расчет с угловыми швами на действие момента в плоскости перпендикулярной плоскости расположения шва

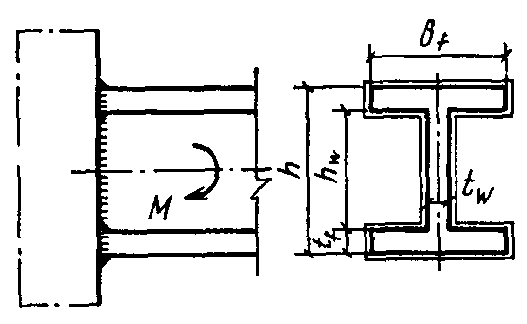
Консоль двутаврового профиля прикрепляется угловым швом путем обварки по периметру профиля. Размеры поперечного сечения показаны на рис. 1

Изгибающий момент $M = 75$ кНм. Материал консоли - листовая сталь марки 15ХСНД $R_ { yn } = 345$ МПа, $R_ { un } = 490$ МПа. Сварка выполняется полуавтоматом в углекислом газе проволокой диаметром 2 мм марки Св-08Г2С в нижнем положении $R_ { wf } = 215$ МПа, $\beta _ { f } = 0,9$. Коэффициенты условий работы $\gamma _ { wf } =\gamma _ { c } = 1$.

Необходимо определить катет углового шва.

Решение

Сечение, по которому следует производить расчет сварного соединения для указанного сочетания стали, сварочной проволоки и способа сварки - по металлу шва. Расчет должен выполняться по формуле $M / W_ { f } \leqslant R_ { wf } \gamma _ { wf } \gamma _ { c } $.

Момент сопротивления расчетного сечения периметра швов

$W_ { f } =I_ { f } / y_ { max } $,

где момент инерции расчетного сечения $ I_f \approx \beta _f \left[ { \frac { 2h_w^3 k_f } { 12 } +2b_f k_f \left( { \frac { h+k_f } { 2 } }\right)^2+2(b_f -t_w )k_f \left( { \frac { h_w -k_f } { 2 } }\right)^2 }\right]; $ $y_ { max } =h / 2 + k_ { f } $.

Для углового шва $k_ { f } = 10$ мм:

$I_ { f } = 0,9 { \ { } 2 \cdot 24^ { 3 } \cdot 1/12 + 2 \cdot 18 \cdot 1 [25,6 + 1) / 2]^ { 2 } + 2 (18 - 0,6) 1 [(24 - 1) / 2]^ { 2 } { \ } } = 11946 см^ { 4 } $;

$y_ { max } = 25,6 / 2 + 1 = 13,8 см; W_ { f } = 11946,9 / 13,8 = 866 см^ { 3 } $.

Напряжение в шве:

$\tau _ { f } =М / W_ { f } = 75 \cdot 10^ { 3 } / 866 = 86,6$ МПа;

$\tau _ { f } / R_ { wf } = 86,6 / 215 = 0,4$.

Таким образом, при $k_ { f } $ = 10 мм напряжение условного среза в соединении $\tau _ { f } $ в 0,4 раза ниже расчетного сопротивления $R_ { wf } $. Следовательно, катет углового шва в соединении должен быть принят $k_ { f } $ = 4 мм.

Рис. 1. К примеру расчета сварного соединения с угловыми швами на действие момента в плоскости, перпендикулярной плоскости расположения швов

$b_ { f } = 18 см; t_ { f } = 0,8 см; t_ { w } = 0,6 см; h_ { w } = 24 см; h = 25,6 см$

$l_ { 1 } = 30$ см; $l_ { 2 } = 20$ см

Проверка прочности соединения при $k_ { f } $ = 4 мм показывает правильность расчета:

$I_ { f } = 4764 см^ { 4 } ; y_ { max } = 13,2 см; W_ { f } = 361 см^ { 3 } ; \tau _ { f } =M / W_ { f } = 75 \cdot 10^ { 3 } / 361 = 208 < 215$ МПа.