Примеры расчета сварных соединений

Расчет сварного соединения с угловыми швами на действие момента в плоскости, перпендикулярной плоскости расположения шва

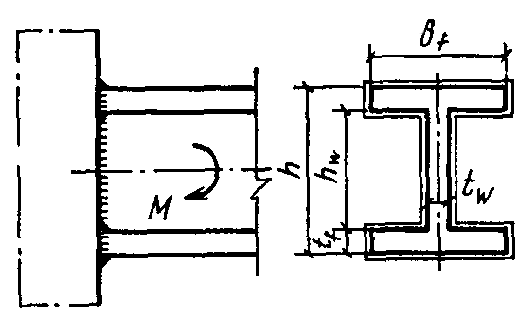
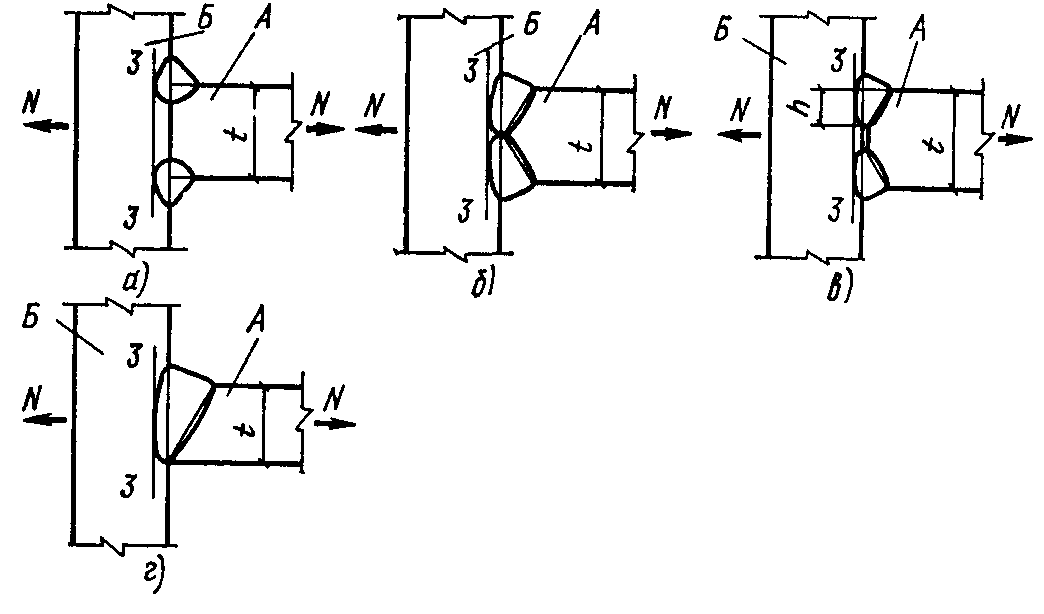
Консоль двутаврового профиля прикрепляется угловым швом путем обварки по периметру профиля. Размеры поперечного сечения показаны на рис. 1

Изгибающий момент $M = 75$ кНм. Материал консоли - листовая сталь марки 15ХСНД $R_ { yn } = 345$ МПа, $R_ { un } = 490$ МПа. Сварка выполняется полуавтоматом в углекислом газе проволокой диаметром 2 мм марки Св-08Г2С в нижнем положении $R_ { wf } = 215$ МПа, $\beta _ { f } = 0,9$. Коэффициенты условий работы $\gamma _ { wf } =\gamma _ { c } = 1$.

Необходимо определить катет углового шва.

Решение

Сечение, по которому следует производить расчет сварного соединения для указанного сочетания стали, сварочной проволоки и способа сварки - по металлу шва. Расчет должен выполняться по формуле $M / W_ { f } \leqslant R_ { wf } \gamma _ { wf } \gamma _ { c } $.

Момент сопротивления расчетного сечения периметра швов

$W_ { f } =I_ { f } / y_ { max } $,

где момент инерции расчетного сечения $ I_f \approx \beta _f \left[ { \frac { 2h_w^3 k_f } { 12 } +2b_f k_f \left( { \frac { h+k_f } { 2 } }\right)^2+2(b_f -t_w )k_f \left( { \frac { h_w -k_f } { 2 } }\right)^2 }\right]; $ $y_ { max } =h / 2 + k_ { f } $.

Для углового шва $k_ { f } = 10$ мм:

$I_ { f } = 0,9 { \ { } 2 \cdot 24^ { 3 } \cdot 1/12 + 2 \cdot 18 \cdot 1 [25,6 + 1) / 2]^ { 2 } + 2 (18 - 0,6) 1 [(24 - 1) / 2]^ { 2 } { \ } } = 11946 см^ { 4 } $;

$y_ { max } = 25,6 / 2 + 1 = 13,8 см; W_ { f } = 11946,9 / 13,8 = 866 см^ { 3 } $.

Напряжение в шве:

$\tau _ { f } =М / W_ { f } = 75 \cdot 10^ { 3 } / 866 = 86,6$ МПа;

$\tau _ { f } / R_ { wf } = 86,6 / 215 = 0,4$.

Таким образом, при $k_ { f } $ = 10 мм напряжение условного среза в соединении $\tau _ { f } $ в 0,4 раза ниже расчетного сопротивления $R_ { wf } $. Следовательно, катет углового шва в соединении должен быть принят $k_ { f } $ = 4 мм.

Рис. 1. К примеру расчета сварного соединения с угловыми швами на действие момента в плоскости, перпендикулярной плоскости расположения швов

$b_ { f } = 18 см; t_ { f } = 0,8 см; t_ { w } = 0,6 см; h_ { w } = 24 см; h = 25,6 см$

$l_ { 1 } = 30$ см; $l_ { 2 } = 20$ см

Проверка прочности соединения при $k_ { f } $ = 4 мм показывает правильность расчета:

$I_ { f } = 4764 см^ { 4 } ; y_ { max } = 13,2 см; W_ { f } = 361 см^ { 3 } ; \tau _ { f } =M / W_ { f } = 75 \cdot 10^ { 3 } / 361 = 208 < 215$ МПа.

Расчет сварного соединения с угловыми швами на действие момента в плоскости расположения швов

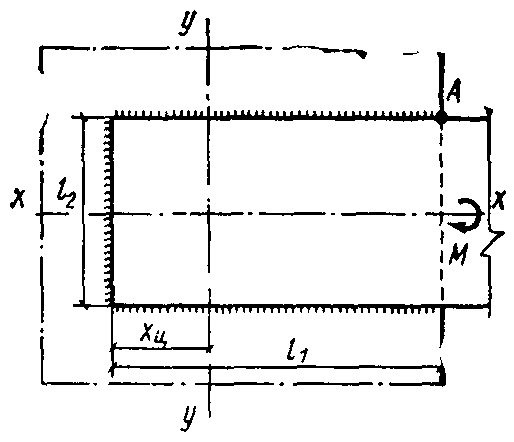
Полоса прикрепляется двумя горизонтальными и одним вертикальным швом { рис. 2 } .

Изгибающий момент $M = 55$ кНм. Материал пластины - сталь марки ВСт3 $R_ { un } = 370$ МПа. Сварка выполняется покрытыми электродами типа Э46 $R_ { wf } = 200$ МПа, $\beta _ { f } = 0,7$. Коэффициенты условий работы $\gamma _ { wf } =\gamma _ { c } = 1$. Необходимо определить катет углового шва.

Решение

Для указанного сочетания стали, электродов и способа сварки расчетным сечением является сечение по металлу шва, поэтому расчет должен выполняться по формуле: $M/(I_ { fx } +I_ { fy } )\sqrt { x^2+y^2 } \leqslant R_ { wf } \gamma _ { wf } \gamma _c$

Рис. 2. К примеру расчета сварного соединения с угловыми швами на действие момента в плоскости расположения швов

Центр тяжести периметра швов определяется по формуле

$x_ { \mbox { ц } } = (l^ { 2 } _ { 1 } - 0,5 l_ { 2 } k_ { f } ) / (2l_ { 1 } +l_ { 2 } )$.

При $k_ { f } = 10$ мм $х_ { \mbox { ц } } = (900 - 0,5 \cdot 20) / (60 + 20) = 11$ см.

Координаты точки $A$, наиболее удаленной от центра тяжести расчетного сечения швов, $х = 19$ см, $у = 10$ см.

Моменты инерции расчетного сечения соединения по металлу шва относительно его главных осей:

$I_ { fx } \approx \beta_ { f } { \ { } l^ { 3 } _ { 2 } k_ { f } / l_ { 2 } + 2l_ { 1 } k_ { f } [(l_ { 2 } +k_ { f } ) / 2]^ { 2 } { \ } } $; $I_ { fy } \approx \beta _f \left[{ 2\left[ { \frac { l_1^3 k_f } { 12 } +l_1 k_f \left( { \frac { l_1 } { 2 } -x_ц }\right)^2 }\right]+l_2 k_f \left( { x_ц +\frac { k_f } { 2 } }\right)^2 }\right]$

Для углового шва $k_ { f } = 10$ мм с учетом того, что расчетная длина шва принимается меньше его полной длины на 10 мм $(l_ { 1 } = 29 см)$:

$I_ { fx } = 0,7 { \ { } 20^ { 3 } \cdot 1/12 + 2 \cdot 29 \cdot 1 [(20 + 1) / 2]^ { 2 } { \ } } = 4942 см^ { 4 } $;

$I_ { fy } = 0,7 { \ { } 2[29^ { 3 } \cdot 1/12 + 29 \cdot 1 (29 / 2 - 11)^ { 2 } ] + 20 \cdot 1 (11 + 1/2)^ { 2 } { \ } } = 5194 см^ { 4 } $;

Расстояние от центра тяжести периметра швов до точки $A$

$\sqrt { x^2+y^2 } =\sqrt { 11^2+10^2 } =21,5$ см.

Напряжения в соединении:

$\tau _ { f } = 55 \cdot 10^ { 3 } \cdot 21,5 / (4942 + 5194) = 117$ МПа.

$\tau _ { f } / R_ { wf } = 117 / 200 = 0,58$.

Таким образом, при $k_ { f } = 10$ мм напряжения в соединении $\tau _ { f } $ составляют 0,58 от расчетного сопротивления $(R_ { wf } )$. Следовательно, катет шва в соединении должен быть принят $k_ { f } = 5,8$ мм $\approx 6$ мм.

Проверка прочности соединения при $k_ { f } = 6$ мм показывает правильность расчета:

$I_ { fx } = 2864 см^ { 4 } ; I_ { fy } = 3078 см^ { 4 } ; \sqrt { x^2+y^2 } = 21,5$ см.

$\tau _ { f } = 55 \cdot 10^ { 3 } \cdot 21,5 / 5942 = 199 < 200$ МПа.

Расчет сварного соединения с угловыми швами на одновременное действие продольной и поперечной сил

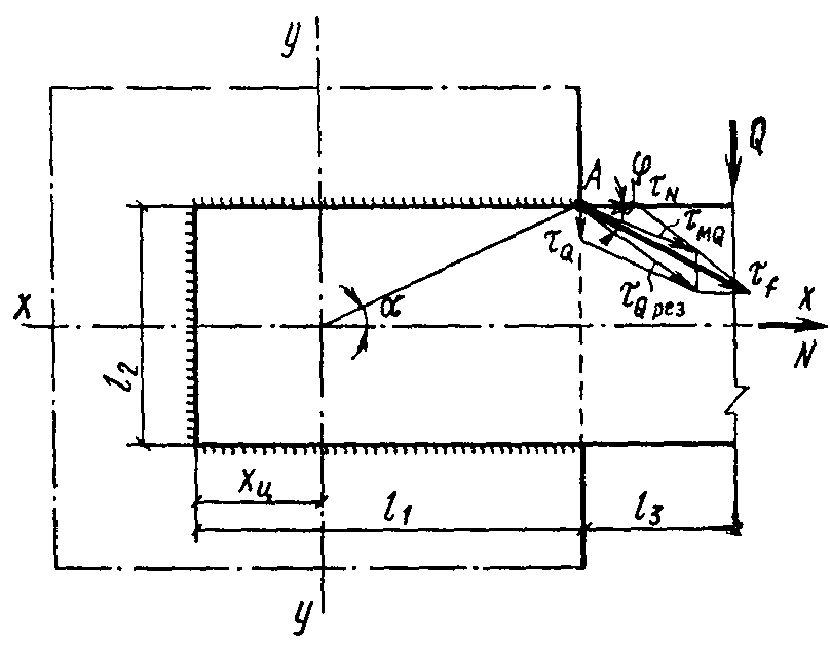
Полоса прикрепляется двумя горизонтальными и одним вертикальным швом { рис. 3 } . Продольная сила $N = 100$ кН, поперечная сила $Q = 38$ кН. Материал пластины - сталь марки ВСт3 $R_ { un } = 370$ МПа. Сварка выполняется покрытыми электродами типа Э46 $R_ { wf } = 200$ МПа, $\beta_ { f } = 0,7$. Коэффициенты условий работы $\gamma _ { wf } =\gamma _ { c } = 1$.

Необходимо определить катет углового шва.

Решение

Для указанного сочетания стали, электродов и способа сварки расчетным сечением является сечение по металлу шва. Поэтому расчет должен выполняться по формуле: $\tau _ { f } \leqslant R_ { wf } \gamma _ { wf } \gamma _ { c } $.

Принимаем $k_ { f } = 10$ мм.

1). Определяем напряжение в соединении от продольной силы $N\tau _ { N } =N / A_ { w } $, где расчетная площадь шва $A_ { w } = (2l_ { 1 } +l_ { 2 } ) k_ { f } \beta _ { f } $.

Рис. 3. К расчету сварного соединения с угловыми швами на одновременное действие продольной и поперечной сил $l_ { 1 } = 30$ см; $l_ { 2 } = 20$ см; $l_ { 3 } = 81$ см

С учетом того, что расчетная длина шва принимается меньше его полной длины на 10 мм:

$A_ { w } = (2 \cdot 29 + 20) 1 \cdot 0,7 = 54,6 см^ { 2 } $,

$\tau _ { N } = 100 \cdot 10 / 54,6 = 18,3$ МПа.

2). Определяем напряжение в соединении от поперечной силы $Q$.

Результирующее напряжение $\tau _ { Q рез } $ является суммой векторов напряжения от силы $Q$, перенесенной в центр тяжести периметра швов $\tau _ { Q } $ и напряжения от момента $\tau _ { мQ } $:

$\tau _ { Q } =Q / A_ { w } = 38 \cdot 10 / 54,6 = 7$ МПа;

$ \tau _ { мQ } =M/(I_ { fx } +I_ { fy } ^ )\sqrt { x^2+y^2 } $

Центр тяжести периметра швов определяется по формуле

$x_ { \mbox { ц } } = (l^ { 2 } _ { 1 } - 0,5l_ { 2 } k_ { f } ) / (2l_ { 1 } +l_ { 2 } ) = (900 - 0,5 \cdot 20 \cdot 1) / (60 + 20) = 11$ см.

Координаты точки $А$, наиболее удаленной от центра тяжести расчетного сечения швов: $x = 19$ см, $у = 10$ см.

Моменты инерции расчетного сечения соединения по металлу шва относительно его главных осей:

$I_ { fx } \approx \beta _ { f } { \ { } l^ { 3 } _ { 2 } k_ { f } / 12 + 2l_ { 1 } k_ { f } [(l_ { 2 } +k_ { f } ) / 2]^ { 2 } { \ } } = \\ = 0,7 { \ { } 20^ { 3 } \cdot 1/12 + 2 \cdot 29 \cdot 1[(20 + 1) / 2]^ { 2 } { \ } } = 4942$ см$^ { 4 } $,

$I_ { fy } \approx \beta _ { f } { \ { } 2 [l^ { 3 } _ { 1 } k_ { f } / 12 + l_ { 1 } k_ { f } (l_ { 1 } / 2 - x_ { \mbox { ц } } )^ { 2 } ] + l_ { 2 } k_ { f } (x_ { \mbox { ц } } +k_ { f } / 2)^ { 2 } { \ } } = \\ = 0,7 { \ { } 2 [29^ { 3 } \cdot 1/12 + 29 \cdot 1 (29 / 2 - 11)^ { 2 } ] + 20 \cdot 1 (11 + 1 / 2)^ { 2 } { \ } } = 5194$ см$^ { 4 } $.

Расстояние точки шва, наиболее удаленной от центра тяжести расчетного сечения соединения:

$\sqrt { x^2+y^2 } =\sqrt { 19^2+10^2 } =21,5$ см.

$\tau _ { мQ } = 38 \cdot 1 \cdot 10^ { 3 } / (4942 + 5194) 21,5 = 80,6$ МПа.

Результирующее напряжение от действия поперечной силы $Q$:

$\tau _ { Q { рез } } =\sqrt { \tau _ { Q } ^2 +\tau _ { мQ } ^2 +2\tau _ { Q } \tau _ { мQ } \cos \alpha } $ ,

где $\alpha $ - угол, определяемый размерами соединения { см. рис. \href { } { 16 } );

$\tau _ { Q { рез } } =\sqrt { 7^2 +80,6^2 +2\cdot 7\cdot 80,6\cdot 0,89 } =86,9$ МПа.

3). Определяем угол между векторами $\vec { \tau } _N $ и $\vec { \tau } _ { Q { рез } } $.

Угол $\phi $ определяют, пользуясь координатным методом на плоскости и свойством скалярного произведения двух векторов: $ \cos \varphi =\vec { a } \vec { b } /\left( { \left| { \vec { a } }\right|\cdot \left| { \vec { b } }\right| }\right), $ где $\vec { a } $ и $\vec { b } $ - векторы; $\vert \vec { a } \vert $ и $\vert \vec { b } \vert $ - длины векторов.

Поскольку скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов $\vec { a } \cdot \vec { b } =x_ { 1 } x_ { 2 } +y_ { 1 } y_ { 2 } $ и длина вектора равна $ \left| { \vec { a } }\right|=\sqrt { x_1^2 +y_1^2 } ; \left| { \vec { b } }\right|=\sqrt { x_2^2 +y_2^2 } , \cos \varphi =\left( { x_1 x_2 +y_1 y_2 }\right)/\left( { \sqrt { x_1^2 +y_1^2 } \sqrt { x_2^2 +y_2^2 } }\right). $

В рассматриваемом примере координаты вектора $\vec { \tau } _N : х_ { 1 } = \tau _ { N } , y_ { 1 } = 0$; координаты вектора $\vec { \tau } _ { Q { рез } } : x_ { 2 } =\tau _ { yQ } sin \alpha , y_ { 2 } =\tau _ { yQ } cos \alpha +\tau _ { Q } $:

$\cos \varphi =\tau _ { мQ } \sin \alpha /\sqrt { (\tau _ { мQ } \sin \alpha )^2+(\tau _ { мQ } \cos \alpha +\tau _Q )^2 } = 80,6\cdot 0,46/\sqrt { (80,6\cdot 0,46)^2+(80,6\cdot 0,89+7,3)^2 } =0,43$

4). Определяем суммарное напряжение в соединении

$\tau _f =\sqrt { \tau _N^2 +\tau _ { Q { рез } } ^2 +2\tau _N \tau _ { Q { рез } } \cos \varphi } = \sqrt { 18,3^2+86,9^2+2\cdot 18,3\cdot 86,9\cdot 0,43 } =96,2$ МПа

$\tau _ { f } / R_ { wf } = 96,2 / 200 = 0,48$.

Таким образом, при $k_ { f } = 10$ мм суммарное напряжение в $0,48$ раза меньше расчетного сопротивления. Следовательно, катет шва в соединении следует принять $k_ { f } = 5$ мм.

$l_ { 1 } = 20$ см; $l_ { 2 } = 16$ см; $l_ { 3 } = 90$ см

Проверка прочности соединения при $k_ { f } = 5$ мм показывает правильность расчета:

$А_ { w } = 27,3 см^ { 2 } ; \tau _ { N } = 100 \cdot 10 / 27,3 = 36,6$ МПа;

$\tau _ { Q } = 38 \cdot 10 / 27,3 = 13,9 МПа; I_ { fx } = 2366 см^ { 4 } ; I_ { fy } = 2557$ см$^ { 4 } $;

$\tau _ { мQ } = 38 \cdot 10^ { 3 } \cdot 21,5 / 4923 = 166$ МПа;

$\tau _ { Q { рез } } =\sqrt { 13,9^2 +166^2 +2\cdot 13,9\cdot 166\cdot 0,89 } =179$ МПа; $cos \phi = 0,43$;

$\tau _f =\sqrt { 36,6^2+179^2+2\cdot 36,6\cdot 179\cdot 0,43 } =198 МПа < 200$ МПа.

Расчет сварного соединения с угловыми швами на одновременное действие продольной и поперечной сил и момента

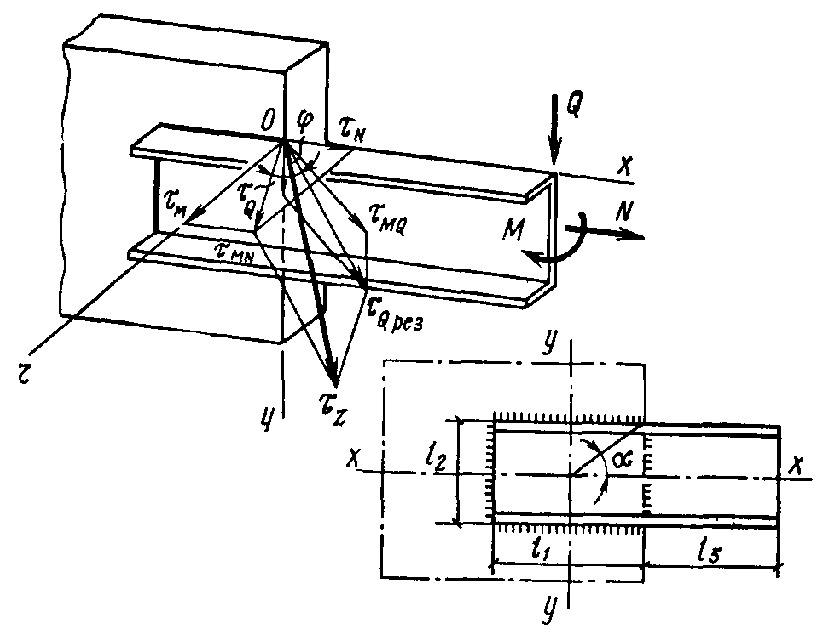
Консоль, подвергающаяся действию продольной и поперечной сил и момента, прикрепляется угловым швом по периметру соприкасающихся поверхностей { рис. 4 } .

Продольная сила $N = 195$ кН, поперечная сила $Q = 30$ кН, изгибающий момент $М = 24,5$ кНм. Материал консоли - сталь марки 18пс $R_ { un } = 370$ МПа, $R_ { wz } = 165$ МПа. Сварка выполняется полуавтоматом в углекислом газе проволокой диаметром 2 мм марки Св-08Г2С в нижнем положении $R_ { wf } = 215$ МПа; $\beta _ { f } = 0,9; \beta _ { z } = 1,05$. Коэффициенты условий работы $\gamma _ { wz } =\gamma _ { c } = 1$.

Рис. 4. К расчету сварного соединения с угловыми швами на одновременное действие продольной и поперечной сил и момента

Необходимо определить катет углового шва.

Решение

Сечение, по которому следует производить расчет сварного соединения для указанного сочетания стали, сварочной проволоки и способа сварки - по металлу границы сплавления. Принимаем $k_ { f } = 10$ мм.

1). Определяем напряжение в соединении от продольной силы $N:\tau _ { N } =N / A_ { w } $, где расчетная площадь шва $A_ { w } = 2 (l_ { 1 } +l_ { 2 } ) k_ { f } \beta _ { z } $.

С учетом того, что расчетная длина шва принимается меньше его полной длины на 10 мм $l_ { 1 } = 19,5$ см, $l_ { 2 } = 15,5$ см:

$A_ { w } = 2(19,5 + 15,5) \cdot 1 \cdot 1,05 = 73,5$ см$^ { 2 } $.

$\tau _ { N } = 195 \cdot 10 / 73,5 = 26,5$ МПа.

2). Определяем напряжение в соединении от поперечной силы $Q$.

Результирующее напряжение $\tau _ { Q рез } $ является суммой векторов напряжения от силы $Q$, перенесенной в центр тяжести периметра швов $(\tau _ { Q } )$ и напряжения от момента $(\tau _ { мQ } )$:

$\tau _ { Q } =Q / A_ { w } = 30 \cdot 10 / 73,5 = 4,1$ МПа; $ \tau _ { мQ } =M\sqrt { x^2+y^2 } /\left( { I_ { zx } +I_ { zy } }\right). $

Моменты инерции расчетного сечения соединения по металлу границы сплавления относительно его главных осей:

$I_ { zx } \approx \beta _ { z } { \ { } 2l^ { 3 } _ { 2 } k_ { f } / 12 + 2l_ { 1 } k_ { f } [(l_ { 2 } +k_ { f } ) / 2]^ { 2 } { \ } } = \\ = 1,05 { \ { } 2 \cdot 15,5^ { 3 } \cdot 1/12 + 2 \cdot 19,5 \cdot 1[(15,5 + 1) / 2]^ { 2 } { \ } } = 3439$ см$^ { 4 } $,

$I_ { zy } \approx \beta _ { z } { \ { } 2l^ { 3 } _ { 1 } k_ { f } / 12 + 2l_ { 2 } k_ { f } [(l_ { 1 } +k_ { f } ) / 2]^ { 2 } { \ } } = \\ = 1,05 { \ { } 2 \cdot 19,5^ { 3 } \cdot 1/12 + 2 \cdot 15,5 \cdot 1 [(19,5 + 1) / 2]^ { 2 } { \ } } = 4717$ см$^ { 4 } $.

Расстояние точки шва, наиболее удаленной от центра тяжести расчетного сечения соединения:

$\sqrt { x^2+y^2 } =\sqrt { 10^2+8^2 } =12,8$ см.

$\tau _ { мQ } = 30 \cdot 10^ { 3 } \cdot 12,8 / 8156 = 47$ МПа.

Результирующее напряжение от действия поперечной силы в плоскости $XOY$:

$\tau _ { Q { рез } } =\sqrt { \tau _Q^2 +\tau _ { мQ } ^2 +2\tau _Q \tau _ { мQ } \cos \alpha } $ ,

где $\alpha $ - угол, определяемый размерами соединения (см. рис. \href { } { 17 } ).

$\tau _ { Q { рез } } =\sqrt { 4,1^2 +47^2 +2\cdot 4,1\cdot 47\cdot 0,78 } =50,3$ МПа.

3). Определение напряжения в соединении от момента $М$:

$\tau _ { м } =Мy_ { max } / I_ { zy } $;

$y_ { max } =l_ { 1 } / 2 + k_ { f } = 20 / 2 + 1 = 11$ см;

$\tau _ { м } = 24,5 \cdot 10^ { 3 } \cdot 11 / 4717 = 57$ МПа.

4). Результирующее напряжение от действия продольной силы $N$ и момента $М $ в плоскости $XOZ$:

$\tau _ { мN } =\sqrt { \tau _м^2 +\tau _N^2 } =\sqrt { 57^2 +26,5^2 } =62,8$ МПа.

5). Определение угла между векторами $\vec { \tau } _ { мN } $ и $\vec { \tau } _ { Q { рез } } $.

Угол $\phi $ определяют, пользуясь координатным методом в пространстве и свойством скалярного произведения двух векторов: $ \cos \varphi =\vec { a } \vec { b } /\left( { \left| { \vec { a } }\right|\cdot \left| { \vec { b } }\right| }\right), $ где $\vec { a } $ и $\vec { b } $ - векторы; $\vert \vec { a } \vert $ и $\vert \vec { b } \vert $ - длины векторов.

Поскольку скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов $\vec { a } \cdot \vec { b } =x_ { 1 } x_ { 2 } +y_ { 1 } y_ { 2 } $ и длина вектора равна корню квадратному из суммы квадратов его координат $\left| { \vec { a } }\right|=\sqrt { x_1^2 +y_1^2 +z_1^2 } , \cos \varphi =\left( { x_1 x_2 +y_1 y_2 +z_1 z_2 }\right)/\left( { \sqrt { x_1^2 +y_1^2 +z_1^2 } \sqrt { x_2^2 +y_2^2 +z_2^2 } }\right)$.

В рассматриваемом примере координаты вектора $\vec { \tau } _ { мN } $:

$х_ { 1 } = \tau _ { N } ; y_ { 1 } = 0; z_ { 1 } =\tau _ { м } $;

координаты вектора $\vec { \tau } _ { Q { рез } } $:

$x_ { 2 } =\tau _ { мQ } sin \alpha ; y_ { 2 } =\tau _ { мQ } cos \alpha +\tau _ { Q } ; z_ { 2 } = 0$; $ \begin{array} { c } \cos \varphi =\tau _N \tau _ { мQ } \sin \alpha /\left[ { \tau _ { мQ } \sqrt { (\tau _ { мQ } \sin \alpha )^2+(\tau _ { мQ } \cos \alpha +\tau _Q )^2 } }\right]= \\ =26,5\cdot 47\cdot 0,625/\left[ { 62,8\sqrt { (47\cdot 0,625)^2+(47\cdot 0,78+4,1)^2 } }\right]=0,25. \\ \end{array} $

6). Определяем суммарное напряжение в соединении

$\tau _z =\sqrt { \tau _ { мN } ^2 +\tau _ { Q { рез } } ^2 +2\tau _ { мN } \tau _ { Q { рез } } \cos \varphi } =\sqrt { 62,8^2+50,3^2+2\cdot 62,8\cdot 50,3\cdot 0,25 } =89,7$ МПа,

$\tau _ { z } / R_ { wz } = 89,7 / 165 = 0,54$.

Таким образом, при $k_ { f } = 10$ мм суммарное напряжение в 0,54 раза меньше расчетного сопротивления. Следовательно, катет шва в соединении следует принять $k_ { f } $ = 6 мм.

7). Проверяем прочность соединения при $k_ { f } = 6$ мм:

Проверка прочности соединения при $k_ { f } = 5$ мм показывает правильность расчета:

$А_ { w } = 2 (19,5 + 15,5) 0,6 \cdot 1,05 = 44,1$ см$^ { 2 } $;

$\tau _ { N } = 195 \cdot 10 / 44,1 = 44,2$ МПа;

$\tau _ { Q } = 30 \cdot 10 / 44,1 = 6,8$ МПа;

$I_ { zx } = 1983 см^ { 4 } ; I_ { zy } = 2754$ см$^ { 4 } $;

$\tau _ { мQ } = 30 \cdot 10^ { 3 } \cdot 12,8 / 4737 = 81$ МПа;

$\tau _ { Q { рез } } =\sqrt { 6,8^2 +81^2 +2\cdot 6,8\cdot 81\cdot 0,78 } =86,4$ МПа;

$\tau _ { м } = 24,5 \cdot 10^ { 3 } \cdot 10,3 / 2754 = 92$ МПа;

$\tau _ { мN } =\sqrt { 92^2 +44,2^2 } =102$ МПа;

$\cos \varphi =44,2\cdot 81\cdot 0,625/\left[ { 102\sqrt { \left( { 81\cdot 0,625 }\right)^2+\left( { 81\cdot 0,78+6,8 }\right)^2 } }\right]=0,25$;

$\tau _z =\sqrt { 102^2+86,4^2+2\cdot 102\cdot 86,4\cdot 0,25 } =149 < 165$ МПа.

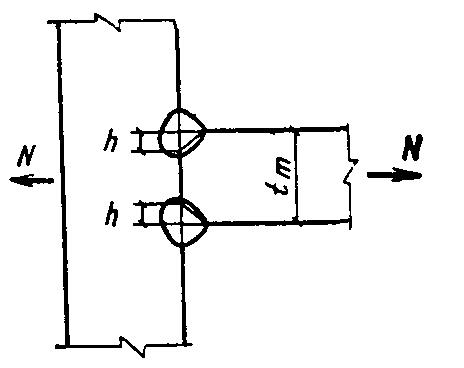
Расчет сварного таврового соединения с разделкой кромок и неполным проваром прикрепляемого элемента на действие растягивающей силы

Элемент толщиной $t_ { m } = 30$ мм и длиной $l = 500$ мм, на которой действует сила $N = 2300$ кН, прикрепляется угловыми швами с разделкой кромок { рис. 5 } . Материал элемента - сталь марки 18Гсп $R_ { wz } = 175$ МПа. Коэффициенты условий работы $\gamma _ { wf } =\gamma _ { wz } = 1; \gamma _ { c } = 0,95$.

Рис. 5. К расчету таврового соединения с разделкой кромок элемента и неполным его проваром

Необходимо выбрать тип электрода для ручной сварки, обеспечивающей требуемую несущую способность соединения.

Расчет соединения производится по формуле, в которой расчетная длина шва $l_ { w } = 500 - 30 = 470$ мм, глубина разделки кромок $h = 10$ мм соединение типа Т9 по ГОСТ 5264-80,

$R_ { wf } \geqslant N / (2,6hl_ { w } \gamma _ { c } ) = 2300 \cdot 10 / (2,6 \cdot 1 \cdot 47 \cdot 0,95) = 198$ МПа.

Выбираем $R_ { wf } = 200$ МПа, соответствующее электродам типа Э46 и Э46А.

Производим проверку прочности по металлу границы сплавления по формуле $2300 \cdot 10 / 2,8 \cdot 1 \cdot 47 \cdot 0,95 = 184$ МПа.

Таким образом, применение электродов типа Э46 и Э46А обеспечивает необходимую несущую способность данного соединения.

Расчет сварного таврового соединения по основному металлу в сечении, перпендикулярном направлению растягивающей силы

Элемент $А$ длиной $l = 200$ мм, на который действует сила $N = 1200$ кН, прикрепляется швом с односторонней разделкой кромки к элементу Б { рис. 6 } . Оба элемента выполнены из листового проката стали марки 10ХСНД толщиной 20 мм $R_ { y } = 355$ МПа, $R_ { u } = 480$ МПа. Коэффициент условий работы $\gamma _ { с } = 1$. Необходимо рассчитать соединение по сечению $3-3$.

Рис. 6. К расчету таврового соединения по основному металлу в сечении, перпендикулярном направлению растягивающей силы

Расчет соединения производится по формуле, в которой длина шва $l_ { w } =l =200$ мм:

$R_ { th } = 0,5 \cdot 480 = 240$ МПа; $N / (1,15tl_ { w } ) = 1200 \cdot 10 / (1,15 \cdot 2 \cdot 20) = 260 > 240$ МПа.

Таким образом, необходимо увеличить толщину $t$ элемента А или длину шва $l_ { w } $. Увеличение необходимо произвести пропорционально соотношению между расчетными сопротивлениями соединяемых элементов следующим образом:

$t^ { A } = 1,74tR^ { A } _ { y } / R^ { \mbox { Б } } _ { u } $ или $l^ { A } _ { w } = 1,74l_ { w } R^ { A } _ { y } / R^ { \mbox { Б } } _ { u } $, где $t^ { A } (l^ { A } _ { w } )$ - толщина { длина } элемента А, выбираемая из условия обеспечения прочности элемента Б по сечению $3-3$.

$t^ { A } = 1,74 \cdot 20 \cdot 355 / 480 = 26$ мм.