Вычисление поверхностного интеграла первого рода

Определение единичного вектора нормали к поверхности. Выражения для элемента площади поверхности

Предположим, что поверхность $\sigma $ задаётся неявным уравнением $\Phi (x,y,z)=0 (\Phi (x,y,z)$ - непрерывно дифференцируемая функция и взаимно однозначно проецируется в область $D_ { xy } $ на плоскости $\mathbf { \textit { Oxy } } $.

Из теории функций нескольких переменных известно, что градиент функции ортогонален поверхности уровня этой функции, проходящей через точку, в которой найден градиент. Рассматривая уравнение $\Phi (x,y,z)=0$ как уравнение поверхности уровня функции трёх переменных $\Phi (x,y,z)$, получаем, что в каждой точке поверхности $\sigma grad\Phi (x,y,z)$ ортогонален $\sigma $, т.е. является нормальным к $\sigma $ вектором.

Чтобы получить единичный нормальный вектор, достаточно просто пронормировать $grad\Phi (x,y,z): \bar { n } =\pm \frac { grad\Phi (x,y,z) } { \vert grad\Phi (x,y,z)\vert } $, где знак перед дробью соответствует возможности выбора двух возможных взаимно противоположных направлений нормали. В координатной форме $\bar { n } =\pm \frac { \frac { \partial \Phi } { \partial x } \bar { i } +\frac { \partial \Phi } { \partial y } \bar { j } +\frac { \partial \Phi } { \partial z } \bar { k } } { \sqrt { \left( { \frac { \partial \Phi } { \partial x } }\right)^2+\left( { \frac { \partial \Phi } { \partial y } }\right)^2+\left( { \frac { \partial \Phi } { \partial z } }\right)^2 } } $, где $\bar { i } ,\bar { j } ,\bar { k } $ - базисные орты.

Если сравнить это выражение с представлением градиента через направляющие косинусы: $\bar { n } =\cos \alpha \bar { i } +\cos \beta \bar { j } +\cos \gamma \bar { k } $, то $\vert \cos \alpha \vert =\frac { \left| { \frac { \partial \Phi } { \partial x } }\right| } { \sqrt { \left( { \frac { \partial \Phi } { \partial x } ^2 }\right)+\left( { \frac { \partial \Phi } { \partial y } ^2 }\right)+\left( { \frac { \partial \Phi } { \partial z } ^2 }\right) } } $, $\vert \cos \beta \vert =\frac { \left| { \frac { \partial \Phi } { \partial y } }\right| } { \sqrt { \left( { \frac { \partial \Phi } { \partial x } ^2 }\right)+\left( { \frac { \partial \Phi } { \partial y } ^2 }\right)+\left( { \frac { \partial \Phi } { \partial z } ^2 }\right) } } $, $\vert \cos \gamma \vert =\frac { \left| { \frac { \partial \Phi } { \partial z } }\right| } { \sqrt { \left( { \frac { \partial \Phi } { \partial x } ^2 }\right)+\left( { \frac { \partial \Phi } { \partial y } ^2 }\right)+\left( { \frac { \partial \Phi } { \partial z } ^2 }\right) } } $.

Теперь мы можем выразить элемент площади поверхности через элемент площади в каждой координатной плоскости: $d\sigma =\frac { dxdy } { \vert \cos \gamma \vert } =\frac { dxdy } { \left| { \frac { \partial \Phi } { \partial z } }\right| } \cdot \sqrt { \left( { \frac { \partial \Phi } { \partial x } }\right)^2+\left( { \frac { \partial \Phi } { \partial y } }\right)^2+\left( { \frac { \partial \Phi } { \partial z } }\right)^2 } $, $d\sigma =\frac { dxdz } { \vert \cos \beta \vert } =\frac { dxdz } { \left| { \frac { \partial \Phi } { \partial y } }\right| } \cdot \sqrt { \left( { \frac { \partial \Phi } { \partial x } }\right)^2+\left( { \frac { \partial \Phi } { \partial y } }\right)^2+\left( { \frac { \partial \Phi } { \partial z } }\right)^2 } $, $d\sigma =\frac { dydz } { \vert \cos \alpha \vert } =\frac { dydz } { \left| { \frac { \partial \Phi } { \partial x } }\right| } \cdot \sqrt { \left( { \frac { \partial \Phi } { \partial x } }\right)^2+\left( { \frac { \partial \Phi } { \partial y } }\right)^2+\left( { \frac { \partial \Phi } { \partial z } }\right)^2 } $.

В частном случае задания уравнения поверхности в явном виде $z=F(x,y)$ получим $z-F(x,y)=0$, т.е. $\Phi (x,y,z)=z-F(x,y)$, $\frac { \partial \Phi } { \partial x } =-\frac { \partial F } { \partial x } $, $\frac { \partial \Phi } { \partial y } =-\frac { \partial F } { \partial y } $, $\frac { \partial \Phi } { \partial z } =1$, поэтому $grad\Phi =-\frac { \partial F } { \partial x } \bar { i } -\frac { \partial F } { \partial y } \bar { j } +\bar { k } $, $\vert grad\Phi \vert =\sqrt { \left( { \frac { \partial F } { \partial x } }\right)^2+\left( { \frac { \partial F } { \partial y } }\right)^2+1 } $, $\cos \gamma =\frac { 1 } { \sqrt { 1+\left( { \frac { \partial F } { \partial x } }\right)^2+\left( { \frac { \partial F } { \partial y } }\right)^2 } } $, и $d\sigma =\frac { dxdy } { \vert \cos \gamma \vert } =\sqrt { 1+\left( { \frac { \partial F } { \partial x } }\right)^2+\left( { \frac { \partial F } { \partial y } }\right)^2 } \cdot dxdy$. Мы уже пользовались этой формулой при вычислении площади поверхности с помощью двойного интеграла.

Выражение поверхностного интеграла через двойной интеграл по проекции поверхности на координатную плоскость

Пусть $\mathbf { } $ поверхность $\sigma $ взаимно однозначно проецируется в область $D_ { xy } $ на плоскости $\mathbf { \textit { Oxy } } $. Будем считать, что поверхность задана уравнением $z=F(x,y)$, $(x,y)\in D_ { xy } $.

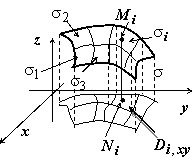
В интегральной сумме $\sum\limits_ { i=1 } ^n { f(M_i )\cdot \sigma _i } $ выразим площадь $\sigma _i $ через двойной интеграл по её проекции $D_ { i,xy } $ на плоскость $\mathbf { \textit { Oxy } } $: $\sigma _i =\iint\limits_ { D_ { i,xy } } { \sqrt { 1+\left( { \frac { \partial F } { \partial x } }\right)^2+\left( { \frac { \partial F } { \partial y } }\right)^2 } dxdy } $.

Применим к этому интегралу теорему о среднем: существует точка $N_i (x_i ,y_i )\in D_ { i,xy } $ такая, что $\sigma _i =\sqrt { 1+\left( { \frac { \partial F } { \partial x } }\right)^2+\left( { \frac { \partial F } { \partial y } }\right)^2 } \left( { N_i }\right)\cdot S(D_ { i,xy } )$. Значение подынтегральной функции $f(x,y,z)$ будем вычислять в точке $M_i (x_i ,y_i ,z_i )$, такой, что $z_i =F(x_i ,y_i )$. Тогда $\sum\limits_ { i=1 } ^n { f(M_i )\cdot \sigma _i } =\sum\limits_ { i=1 } ^n { f(x_i ,y_i ,F(x_i ,y_i ))\cdot \sqrt { 1+\left( { \frac { \partial F } { \partial x } }\right)^2+\left( { \frac { \partial F } { \partial y } }\right)^2 } \left( { (x_i ,y_i ) }\right)\cdot S(D_ { i,xy } ) } $.

Слева стоит интегральная сумма для поверхностного интеграла, справа - для двойного; переход к пределу при $\mathop { \max } \limits_ { i=1,2,\ldots n } diam\sigma _i \to 0$ { при этом и $\mathop { \max } \limits_ { i=1,2,\ldots n } diamD_ { i,xy } \to 0$ } даёт $ \iint\limits_\sigma { f(x,y,z)d\sigma } =\iint\limits_ { D_ { xy } } { f(x,y,F(x,y)) } \cdot \sqrt { 1+\left( { \frac { \partial F } { \partial x } }\right)^2+\left( { \frac { \partial F } { \partial y } }\right)^2 } \cdot dxdy. $

Эта формула и применяется для вычисления поверхностных интегралов. Естественно, в каждой задаче надо выбирать, на какую из координатных плоскостей предпочтительней проецировать поверхность; если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.

Пример 1

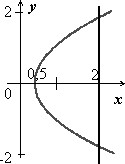
Найти $\iint\limits_\sigma { \sqrt { \frac { x } { 2x-1 } } } d\sigma $, где $\sigma $ - часть цилиндра $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } = 2\mathbf { \textit { x } } $, вырезаемая гиперболоидом $\mathbf { \textit { x } } ^ { 2 } -\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } = 1$ и плоскостью $\mathbf { \textit { z } } = 0 \mathbf { \textit { z } } > 0$.

Решение

Найдем проекцию поверхности $\sigma $ на плоскость $\mathbf { \textit { OXY } } $. Исключим из уравнений цилиндра и гиперболоида переменную $\mathbf { \textit { z } } $:

$\left\ { { \begin{array} { l } x^2+z^2=2x \\ x^2-y^2+z^2=1 \\ \end{array} }\right.\Rightarrow 2\mathbf { \textit { x } } =\mathbf { \textit { y } } ^ { 2 } +1$ - уравнение проекции линии пересечения двух поверхностей на $\mathbf { \textit { OXY } } $.

Полагая в уравнении цилиндра $\mathbf { \textit { z } } = 0$, получим уравнение линии пересечения цилиндра и плоскости $\mathbf { \textit { OXY } } $. Таким образом, поверхность $\sigma $ проецируется в область $\mathbf { \textit { D } } $, ограниченную параболой $\mathbf { \textit { x } } =\frac { 1 } { 2 } (\mathbf { \textit { y } } ^ { 2 } +1)$ и прямой $\mathbf { \textit { x } } =2$.

Часть цилиндра, удовлетворяющая условию $\mathbf { \textit { z } } >0$, задается уравнением $\mathbf { \textit { z } } =\sqrt { 2x-x^2 } $. Тогда $\frac { \partial z } { \partial x } =\frac { 1-x } { \sqrt { 2x-x^2 } } ,\frac { \partial z } { \partial y } =0, \sqrt { 1+\left( { \frac { \partial z } { \partial x } }\right)^2+\left( { \frac { \partial z } { \partial y } }\right)^2 } =\sqrt { 1+\frac { (1-x)^2 } { 2x-x^2 } } =\frac { 1 } { \sqrt { 2x-x^2 } } $.

Таким образом, $\iint\limits_\sigma { \sqrt { \frac { x } { 2x-1 } } } d\sigma =\iint\limits_D { \sqrt { \frac { x } { 2x-1 } } } \cdot \frac { 1 } { \sqrt { 2x-x^2 } } dxdy=2\int\limits_ { 1/2 } ^2 { \frac { dx } { \sqrt { 2x-1 } \cdot \sqrt { 2-x } } \cdot \int\limits_0^ { \sqrt { 2x-1 } } { dy= } } 2\int\limits_ { 1/2 } ^2 { \frac { dx } { \sqrt { 2-x } } = } \left. { 4\sqrt { 2-x } }\right|_2^ { 1/2 } =4\sqrt { \frac { 3 } { 2 } } $.

Пример 2

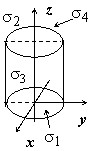
Найти $\iint\limits_\sigma { z\left| { xy }\right|d\sigma } $, где $\sigma $ - полная поверхность цилиндра $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } = 1, 0\leq \mathbf { \textit { z } } \leq 1$.

Решение

Искомый интеграл равен сумме трех интегралов: по нижнему и верхнему основаниям $\sigma _ { 1 } $ и $\sigma _ { 2 } $ и боковой поверхности. Так как на нижнем основании $z=0$, то $\iint\limits_ { \sigma _1 } { z\left| { xy }\right|d\sigma } =0$. Для верхнего основания $\sigma _ { 2 } $ имеем $\mathbf { \textit { z } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } )=1, \frac { \partial z } { \partial x } =\frac { \partial z } { \partial y } =0$, поэтому поверхностный интеграл по $\sigma _ { 2 } $ совпадает с двойным интегралом от функции $\mathbf { \textit { z } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } )\vert \mathbf { \textit { xy } } \vert =\vert \mathbf { \textit { xy } } \vert $, взятым по кругу $\mathbf { \textit { D } } = { \ { } \mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } <1 { \ } } $:

$ \iint\limits_ { \sigma _2 } { z\left| { xy }\right|d\sigma } =\iint\limits_D { \left| { xy }\right|dxdy=4\int\limits_0^ { \pi /2 } { \cos \varphi \sin \varphi d\varphi \cdot \int\limits_0^1 { r^3dr } =4\left. { \frac { \sin ^2\varphi } { 2 } }\right|_0^ { \pi /2 } \cdot \left. { \frac { r^4 } { 4 } }\right|_0^1 =\frac { 1 } { 2 } } } $

Найдем интеграл по боковой поверхности. Она состоит из двyх частей: $\sigma _ { 3 } $ и $\sigma _ { 4 } $ , симметричных относительно плоскости $\mathbf { \textit { OYZ } } $. Так как фyнкция $\mathbf { \textit { z } } \vert \mathbf { \textit { xy } } \vert $ - четная по $\mathbf { \textit { x } } $, то интегралы по $\sigma _ { 3 } $ и $\sigma _ { 4 } $ равны.

Проекция $\sigma _ { 3 } $ на плоскость $\mathbf { \textit { OYZ } } $ - прямоyгольник $\mathbf { \textit { D } } : { \ { } -1 \leq \mathbf { \textit { y } } \leq 1, 0 \leq \mathbf { \textit { z } } \leq 1 { \ } } $.

Уравнение $\sigma _ { 3 } : \mathbf { \textit { x } } =\sqrt { 1-y^2 } , \sqrt { 1+\left( { \frac { \partial x } { \partial y } }\right)^2+\left( { \frac { \partial x } { \partial z } }\right)^2 } =\frac { 1 } { \sqrt { 1-y^2 } } $

Отсюда: $\iint\limits_ { \sigma _3 \cup \sigma _4 } { z\left| { xy }\right|d\sigma } =2\iint\limits_D { z\left| y \right|\sqrt { 1-y^2 } \frac { dydz } { \sqrt { 1-y^2 } } =\int\limits_0^1 { 4zdz\cdot \int\limits_0^1 { ydy } =1 } } $

Окончательно полyчаем: $\iint\limits_\sigma { z\left| { xy }\right|d\sigma } =0+\frac { 1 } { 2 } +1=\frac { 3 } { 2 } $

Пример 3

Найти $\iint\limits_\sigma { x^2d\sigma } $, где $\sigma $ - сфера $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } =\mathbf { \textit { R } } ^ { 2 } $.

Решение

Использование соображений симметрии позволяет иногда существенно упростить вычисление интегралов. Очевидно, что для сферы $\iint\limits_\sigma { x^2d\sigma } =\iint\limits_\sigma { y^2d\sigma } =\iint\limits_\sigma { z^2d\sigma } $. Тогда $ \iint\limits_\sigma { x^2d\sigma } =\frac { 1 } { 3 } \iint\limits_\sigma { (x^2+y^2+z^2)d\sigma } =\frac { 1 } { 3 } R^2\iint\limits_\sigma { d\sigma } =\frac { 4\pi R^4 } { 3 } . $