Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы

Если выполнены условия независимости от формы пути, соединяющего начальную $A(x_1 ,y_1 )$ и конечную $B(x_2 ,y_2 )$ точки кривой, то значение интеграла $\int\limits_ { \mathop { AB } \limits^\cup } { Pdx+Qdy } \mathbf { } $ определяется только точками $\mathbf { \textit { A } } $ и $\mathbf { \textit { B } } $

Поэтому в этом случае для обозначения интеграла применяется обозначение $\int\limits_A^B { Pdx+Qdy } \mathbf { } $ или $\int\limits_ { (x_1 ,y_1 ) } ^ { (x_2 ,y_2 ) } { Pdx+Qdy } $.

Докажем следующую теорему.

Теорема

Если в односвязной области $\mathbf { \textit { G } } $ выполнено условие $\frac { \partial Q } { \partial x } =\frac { \partial P } { \partial y } $, то существует функция $u(x,y)$ такая, что для любых точек $A(x_1 ,y_1 )\in G$ и $B(x_2 ,y_2 )\in G \quad \int\limits_ { (x_1 ,y_1 ) } ^ { (x_2 ,y_2 ) } { Pdx+Qdy } =u(x_2 ,y_2 )-u(x_1 ,y_1 )\mathbf { . } $

Функцию $u(x,y)$ принято называть потенциальной функцией.

Доказательство

Фиксируем произвольную точку $M_0 (x_0 ,y_0 )\in G$, и докажем, что в качестве искомой функции $u(x,y)$ можно взять $u(x,y)=\int\limits_ { (x_0 ,y_0 ) } ^ { (x,y) } { Pdx+Qdy } \mathbf { . } $

Действительно, по свойству аддитивности $\int\limits_ { \mathop { M_0 AB } \limits^\cup } { Pdx+Qdy } =\int\limits_ { \mathop { M_0 A } \limits^\cup } { Pdx+Qdy } +\int\limits_ { \mathop { AB } \limits^\cup } { Pdx+Qdy } \Rightarrow \mathbf { } \int\limits_ { \mathop { AB } \limits^\cup } { Pdx+Qdy } =\mathbf { } =\int\limits_ { \mathop { M_0 AB } \limits^\cup } { Pdx+Qdy } -\int\limits_ { \mathop { M_0 A } \limits^\cup } { Pdx+Qdy } \mathbf { , } $ или $\int\limits_ { (x_1 ,y_1 ) } ^ { (x_2 ,y_2 ) } { Pdx+Qdy } =\int\limits_ { (x_0 ,y_0 ) } ^ { (x_2 ,y_2 ) } { Pdx+Qdy } -\int\limits_ { (x_0 ,y_0 ) } ^ { (x_1 ,y_1 ) } { Pdx+Qdy } \mathbf { , } $т.е. $\int\limits_ { (x_1 ,y_1 ) } ^ { (x_2 ,y_2 ) } { Pdx+Qdy } =u(x_2 ,y_2 )-u(x_1 ,y_1 )$, что и требовалось доказать.

Разность $u(x_2 ,y_2 )-u(x_1 ,y_1 )\mathbf { } $обозначается символом $\left. { u(x,y) }\right|_ { (x_1 ,y_1 ) } ^ { (x_2 ,y_2 ) } \mathbf { } $ или $\left. { u(x,y) }\right|_A^B $.

Формула $\int\limits_ { (x_1 ,y_1 ) } ^ { (x_2 ,y_2 ) } { Pdx+Qdy } =\left. { u(x,y) }\right|_ { (x_1 ,y_1 ) } ^ { (x_2 ,y_2 ) } $ является аналогом формулы Ньютона-Лейбница для двухмерного случая; ещё раз отметим, что она имеет место в случае, когда выполняются условия независимости интеграла от формы пути.

$ { M } '(x+\Delta x,y) M(x,y) M_0 (x_0 ,y_0 ) \bar { x } $

Докажем, что для построенной функции $u(x,y)$ выполняются следующие соотношения:

$\frac { \partial u } { \partial x } =P(x,y),\;\frac { \partial u } { \partial y } =Q(x,y).$

Доказательство

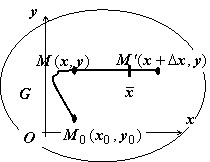
Действительно, пусть $M(x,y)\in G,$

$ { M } '(x+\Delta x,y)\in G.$ Тогда $u(M)=\int\limits_ { \mathop { M_0 M } \limits^\cup } { Pdx+Qdy } $,

$u( { M } ')=\int\limits_ { \mathop { M_0 M { M } ' } \limits^\cup } { Pdx+Qdy } =\int\limits_ { \mathop { M_0 M } \limits^\cup } { Pdx+Qdy } +\int\limits_ { \mathop { M { M } ' } \limits^\cup } { Pdx+Qdy } \Rightarrow u(x+\Delta x,y)=u(x,y)+\int\limits_x^ { x+\Delta x } { P(x,y)dx } $ { на $M { M } 'y=const$ } $\Rightarrow \Delta _x u(x,y)=u(x+\Delta x,y)-u(x,y)= \int\limits_x^ { x+\Delta x } { P(x,y)dx } =P(\bar { x } ,y)\cdot \Delta x$ { по теореме о среднем } $\Rightarrow \frac { \Delta _x u } { \Delta x } =P(\bar { x } ,y)$.

Точка $\bar { x } $ удовлетворяет условиям $x<\bar { x } <x+\Delta x$. Устремим $\Delta x\to 0$, тогда $\bar { x } \to x$, и $\mathop { \lim } \limits_ { \Delta x\to 0 } \frac { \Delta _x u } { \Delta x } =\mathop { \lim } \limits_ { \bar { x } \to x } P(\bar { x } ,y)=P(x,y)$.

Аналогично доказывается, что $\frac { \partial u } { \partial y } =Q(x,y)$.

Условие $\frac { \partial Q } { \partial x } =\frac { \partial P } { \partial y } $ теперь означает просто, что $\frac { \partial ^2u } { \partial x\partial y } =\frac { \partial ^2u } { \partial y\partial x } $.

Кроме того, из $\frac { \partial u } { \partial x } =P(x,y), \quad \frac { \partial u } { \partial y } =Q(x,y),$ следует, что подынтегральное выражение $P(x,y)dx+Q(x,y)dy = \frac { \partial u } { \partial x } dx+\frac { \partial u } { \partial y } dy=du$ является полным дифференциалом функции $u(x,y)$ { условие $\frac { \partial Q } { \partial x } =\frac { \partial P } { \partial y } $ есть условие того, что обыкновенное дифференциальное уравнение первого порядка $P(x,y)dx+Q(x,y)dy=0$ - уравнение в полных дифференциалах } .

Для отыскания потенциальной функции $u(x,y)$ можно:

1. Решить уравнение в полных дифференциалах;
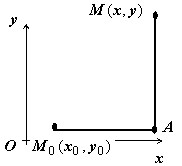
2. Построить $u(x,y)$ напрямую по формуле $u(x,y)=\int\limits_ { (x_0 ,y_0 ) } ^ { (x,y) } { Pdx+Qdy } $. В качестве пути интегрирования обычно берётся путь $\mathbf { \textit { M } } _ { 0 } \mathbf { \textit { AM } } $, состоящий из отрезков, параллельных координатным осям.

Тогда на $\mathbf { \textit { M } } _ { 0 } \mathbf { \textit { A } } y=y_0, dy=0, x_0 \leqslant x$ { как переменная интегрирования } $\leqslant x_M $; на $\mathbf { \textit { AM } } x=x_M ;dx=0, y_0 \leqslant y$ { как переменная интегрирования } $\leqslant y_M $.

Продемонстрируем оба метода на примере $\int\limits_L { 2xydx+(x^2+y^2)dy } $. Здесь $P=2xy, \frac { \partial P } { \partial y } =2x, Q=x^2+y^2, \frac { \partial Q } { \partial y } =2x=\frac { \partial P } { \partial y } $, т.е. условия независимости выполняются. В качестве точки $M_0 $ берём начало координат $M_0 (0,0)$.

1. Решаем систему уравнений $\left[{ \begin{array} { l } \frac { \partial u } { \partial x } =2xy, \\ \frac { \partial u } { \partial y } =x^2+y^2. \\ \end{array} }\right.$ Из первого уравнения $u(x,y)=\int\limits_0^x { 2xydx } =x^2y+\varphi (y)$, подставляем эту функцию во второе уравнение $\frac { \partial u } { \partial y } =x^2+ { \varphi } '(y)=x^2+y^2\Rightarrow { \varphi } '(y)=y^2\Rightarrow \varphi (y)=y^3/3+C\Rightarrow u(x,y)=x^2y+\frac { x^3 } { 3 } +C$ { потенциал всегда определяется с точностью до произвольной постоянной, физический смысл имеет разность потенциалов в двух точках, которая не зависит от этой постоянной } .
2. $u(x,y)=\int\limits_0^x { 2x\cdot 0\cdot dx } +\int\limits_0^y { \left( { x^2+y^2 }\right)dy } =x^2y+\frac { y^3 } { 3 } +C$.

Теперь, когда потенциальная функция определена, легко находится любой интеграл: $\int\limits_ { (0,0) } ^ { (2,4) } { 2xydx+(x^2+y^2)dy } =\left. { \left( { x^2y+\frac { y^3 } { 3 } }\right) }\right|_ { (0,0) } ^ { (2,4) } =16+\frac { 64 } { 3 } -0=37\frac { 1 } { 3 } $.