Вычисление криволинейного интеграла второго рода. Примеры.
Пусть кривая $L$ задана параметрическими уравнениями $L:\left[{ \begin{array} { l } x=x(t), \\ y=y(t), \\ z=z(t); \\ \end{array} }\right.\quad t_0 \leqslant t\leqslant t_k $, где $x(t),\;y(t),\;z(t)$- непрерывно дифференцируемые функции, и пусть точкам $A_i (x_i ,y_i ,z_i )$, которые задают разбиение кривой, соответствуют значения параметра $t_i $, т.е. $x_i =x(t_i ),\;y_i =y(t_i ),\;z_i =z(t_i )$.
Тогда по теореме Лагранжа существуют такие точки $\bar { t } _i \;(i=1,2,\ldots ,n)$, что $\Delta x_i =x_i -x_ { i-1 } = { x } '(\bar { t } _i )(t_i -t_ { i-1 } )$.
Выберем точки $M_i $, получающиеся при этих значениях параметра: $M_i (x_i ,y_i ,z_i )=M_i (x(\bar { t } _i ),y(\bar { t } _i ),z(\bar { t } _i ))$.
Тогда интегральная сумма для криволинейного интеграла $\sum\limits_ { i=1 } ^n { P(x_i ,y_i ,z_i )\cdot \Delta x_i } $ будет равна интегральной сумме для определенного интеграла $\sum\limits_ { i=1 } ^n { P(x(\bar { t } _i ),y(\bar { t } _i ),z(\bar { t } _i ))\cdot { x } '(\bar { t } _i )\cdot \Delta t_i } $.
Так как $\Delta l_i \to 0\Leftrightarrow \Delta t_i \to 0$, то, переходя к пределу при $\mathop { \max } \limits_ { i=1,2,\ldots ,n } \Delta l_i \to 0,\;\mbox { или, } \;\mbox { что } \;\mbox { тоже } \;\mbox { самое } ,\;\mathop { \max } \limits_ { i=1,2,\ldots ,n } \Delta t_i \to 0$ в равенстве $\sum\limits_ { i=1 } ^n { P(x_i ,y_i ,z_i )\cdot \Delta x_i } =\sum\limits_ { i=1 } ^n { P(x(\bar { t } _i ),y(\bar { t } _i ),z(\bar { t } _i ))\cdot { x } '(\bar { t } _i )\cdot \Delta t_i } $, получим
$\int\limits_L { P(x,y,z)\cdot dx } =\int\limits_ { t_0 } ^ { t_k } { P(x(t),y(t),z(t))\cdot { x } '(t)\cdot dt } .$
Аналогично доказываются формулы для интегралов по другим координатам. Окончательно $\begin{array} { l } \int\limits_L { P(x,y,z)\cdot dx+Q(x,y,z)\cdot dy+R(x,y,z)\cdot dz } = \\ =\int\limits_ { t_0 } ^ { t_k } { \left[ { P(x(t),y(t),z(t))\cdot { x } '(t)+Q(x(t),y(t),z(t))\cdot { y } '(t)+R(x(t),y(t),z(t))\cdot { z } '(t) }\right]dt } . \\ \end{array} $
Таким образом, вычисление криволинейного интеграла второго рода ни чем не отличается от вычисления интеграла первого и сводится к интегрированию по параметру. Направление интегрирования определяется условиями задачи .
Пример 1
Найти $\int\limits_ { \mathop { AB } \limits^\cup } { ydx-xdy+zdz } $, где $\mathop { AB } \limits^\cup $ - виток винтовой линии $\mathbf { \textit { x } } =\mathbf { \textit { a } } \cdot \cos \mathbf { \textit { t } } , \mathbf { \textit { y } } =\mathbf { \textit { a } } \cdot \sin \mathbf { \textit { t } } , \mathbf { \textit { z } } =\mathbf { \textit { a } } \cdot \mathbf { \textit { t } } , 0 \leqslant\mathbf { \textit { t } } \leqslant $ 2$\pi $.
Решение:
$\int\limits_ { \mathop { AB } \limits^\cup } { ydx-xdy+zdz } =\int\limits_0^ { 2\pi } { (a\sin t\cdot (-a\sin t)-a\cos t\cdot a\cos t+at\cdot a)dt } =a^2\int\limits_0^ { 2\pi } { (t-1)dt } =2a^2(\pi ^2-\pi )$
Пусть плоская кривая задана в декартовой системе координат уравнением $\mathbf { \textit { y } } =\mathbf { \textit { y } } (\mathbf { \textit { x } } )$, $\mathbf { \textit { A } } (\mathbf { \textit { a } } $,$\mathbf { \textit { y } } (\mathbf { \textit { a } } ))$, $\mathbf { \textit { B } } (\mathbf { \textit { b } } $,$\mathbf { \textit { y } } (\mathbf { \textit { b } } ))$.
Тогда $ \int\limits_ { \mathop { AB } \limits^\cup } { Pdx+Qdy } =\int\limits_a^b { (P(x,y(x))+Q(x,y(x)) { y } '(x))dx } . $
Пример 2
Найти $\int\limits_ { \mathop { AB } \limits^\cup } { (x+y)dx+y^2dy } $ по кривой $\left[{ \begin{array} { l } y=0,\;0\leqslant x\leqslant 1 \\ y=\ln x,\;1\leqslant x\leqslant e \\ \end{array} }\right.$.
Решение:
Пользуясь свойством аддитивности, разобьем интеграл на сумму двух:
$\int\limits_0^1 { (x+o)dx+\int\limits_1^e { (x+\ln x+ } } \ln ^2x\cdot \frac { 1 } { x } )dx=\left. { \frac { x^2 } { 2 } }\right|_0^1 + \left. { (\frac { x^2 } { 2 } +x\ln x-x+ \frac { \ln ^3x } { 3 } ) }\right|_1^e =\frac { e^2 } { 2 } +\frac { 4 } { 3 } $
Пример 3
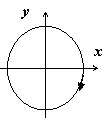
Найти $\oint\limits_c { x(1-y)dx+xdy } $, где $\mathbf { \textit { C } } $ - окружность, проходимая в отрицательном направлении { по часовой стрелке } .
Решение:
Параметризуем окружность $\mathbf { \textit { x } } =2\cos \mathbf { \textit { t } } , \mathbf { \textit { y } } =2\sin \mathbf { \textit { t } } , 0 \leqslant \mathbf { \textit { t } } \leqslant 2\pi $. Движению по часовой стрелке соответствует уменьшение параметра $\mathbf { \textit { t } } $, поэтому интегрируем от $2\pi $ до 0:
$\begin{array} { l } \oint\limits_С { x(1-y)dx+xdy=\int\limits_ { 2\pi } ^0 { (2\cos t(1-2\sin t)(-2\sin t)+2\cos t\cdot 2\cos t)dt=\int\limits_ { 2\pi } ^0 { (-4\cos t\sin t } } } + \\ +8\cos t\cdot \sin ^2t+4\cos ^2t)dt=\left. { (-2\sin ^2t+\frac { 8 } { 3 } \sin ^3t+2t+\sin 2t) }\right|_ { 2\pi } ^0 =-4\pi . \\ \end{array} $
Пример 4
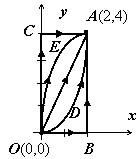
Вычислить $\int\limits_L { 2xydx+(x^2+y^2)dy } $ по каждому из путей, соединяющих точки $\mathbf { \textit { O } } (0,0)$ и $\mathbf { \textit { A } } (2,4)$, и изображённых на рисунке:
- Ломаная $\mathbf { \textit { OBA } } $, состоящая из прямолинейных отрезков;
- Ломаная $\mathbf { \textit { OCA } } $;
- Прямолинейный отрезок $\mathbf { \textit { OA } } $;
- Параболы $\mathbf { \textit { ODA } } $ и $\mathbf { \textit { OEA } } $, симметричные относительно координатных осей.
Решение:
1). $\int\limits_ { OBA } { 2xydx+(x^2+y^2)dy } =\int\limits_ { OB } { 2xydx+(x^2+y^2)dy } + \quad +\int\limits_ { BA } { 2xydx+(x^2+y^2)dy } $ { по свойству аддитивности } . На $\mathbf { \textit { ОВ } } $ в качестве параметра естественно выбрать переменную $\mathbf { \textit { х } } $, при этом $y=0,\;dy=0$, поэтому $\int\limits_ { OB } { 2xydx+(x^2+y^2)dy } =0$.
На $\mathbf { \textit { ВА } } \quad x=2,\;dx=0,\;0\leqslant y\leqslant 4$, поэтому $\int\limits_ { BA } { 2xydx+(x^2+y^2)dy } =\int\limits_0^4 { \left( { 2^2+y^2 }\right)dy } =\left. { \left( { 4y+\frac { y^3 } { 3 } }\right) }\right|_0^4 =37\frac { 1 } { 3 } $.
Окончательно, $I_1 =\int\limits_ { OBA } { 2xydx+(x^2+y^2)dy } =37\frac { 1 } { 3 } $.
2). $\int\limits_ { OCA } { 2xydx+(x^2+y^2)dy } =\int\limits_ { OC } { 2xydx+(x^2+y^2)dy } +\int\limits_ { CA } { 2xydx+(x^2+y^2)dy } $.
$\int\limits_ { OC } { 2xydx+(x^2+y^2)dy } =\left| { x=0,\;dx=0,\;0\leqslant y\leqslant 4 }\right|=\int\limits_0^4 { y^2dy } =\frac { 64 } { 3 } =21\frac { 1 } { 3 } . \\ \int\limits_ { CA } { 2xydx+(x^2+y^2)dy } =\left| { y=4,\;dy=0,\;0\leqslant x\leqslant 2 }\right|=\int\limits_0^2 { 8xdx } =16.$ Окончательно, $I_2 =\int\limits_ { OСA } { 2xydx+(x^2+y^2)dy } =37\frac { 1 } { 3 } $.
3). На прямолинейном отрезке $\mathbf { \textit { OA } } \quad y=2x$, поэтому $\int\limits_ { OA } { 2xydx+(x^2+y^2)dy } =\int\limits_0^2 { \left( { 2x\cdot 2x\cdot 1+(x^2+4x^2)\cdot 2 }\right)dx } =\int\limits_0^2 { 14x^2dx } =\frac { 112 } { 3 } =37\frac { 1 } { 3 } $.
4). Уравнение параболы $\mathbf { \textit { OEA } } $ имеет вид $x=ky^2$, значение коэффициента $\mathbf { \textit { k } } $ найдём, подставляя в это уравнение координаты точки $\mathbf { \textit { А } } $:
$2=k4^2\rightarrow k=1/8\rightarrow x=y^2/8;~x'_y=y/4$, поэтому
$\int\limits_ { OEA } { 2xydx+(x^2+y^2)dy } =\int\limits_0^4 { \left[ { \left( { 2\cdot \frac { y^2 } { 8 } \cdot y }\right)\cdot \frac { y } { 4 } +\left( { \frac { y^4 } { 64 } +y^2 }\right) }\right]dy } =\int\limits_0^4 { \left( { \frac { 5y^4 } { 64 } +y^2 }\right)dy } =37\frac { 1 } { 3 } $.
5). Совершенно также убеждаемся, что интеграл по параболе $\mathbf { \textit { ODA } } $ имеет то же значение.
Закономерен вопрос: для любого ли интеграла и любых начальной и конечной точек значение интеграла не зависит от формы пути, соединяющего эти точки?
Убедимся в том, что это не так, на примере интеграла $\int\limits_L { 2xydx-(x^2+y^2)dy } $: $I_1 =\int\limits_ { OBA } { 2xydx-(x^2+y^2)dy } =-\int\limits_0^4 { (2^2+y^2)dy } =-37\frac { 1 } { 3 } $; $I_2 =\int\limits_ { OCA } { 2xydx+(x^2-y^2)dy } =\int\limits_0^4 { y^2dy } -\int\limits_0^2 { 8xdx } =\frac { 64 } { 3 } -16=5\frac { 1 } { 3 } \ne I_1 $.
Следующие разделы будут посвящены ответу на поставленный вопрос: при каких условиях криволинейный интеграл второго рода $\int\limits_С { Pdx+Qdy } $ не зависит от формы пути, соединяющего начальную и конечную точки, и определяется только этими точками? В трёхмерном случае этот вопрос будет изучаться в теории поля.
Далее:
Класс $T_1$. Теорема о замкнутости класса $T_1$
Вычисление объёмов
Лемма о построении множества $[F]_{x1,x2}$
Решение задач с помощью алгебры высказываний
Замена переменных в тройном интеграле
Теорема об алгоритме распознавания полноты
Вычисление поверхностного интеграла первого рода
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Механические приложения тройного интеграла
Определение тройного интеграла. Теорема существования тройного интеграла
Формула Гаусса - Остроградского
Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Теорема Стокса
Булевы функции от $n$ переменных
Огравление $\Rightarrow $
Комментарии ()