Вычисление криволинейного интеграла первого рода. Примеры

Пусть кривая $L$ задана параметрическими уравнениями

$L:\left[{ \begin{array} { l } x=x(t), \\ y=y(t), \\ z=z(t); \\ \end{array} }\right.\quad t_0 \leqslant t\leqslant t_k $, где $x(t),\;y(t),\;z(t)$- непрерывно дифференцируемые функции, и пусть точкам $A_i (x_i ,y_i ,z_i )$, которые задают разбиение кривой, соответствуют значения параметра $t_i $, т.е. $x_i =x(t_i ),\;y_i =y(t_i ),\;z_i =z(t_i )$. Тогда { см. Вычисление длин кривых } $\Delta l_i =\int\limits_ { t_ { i-1 } } ^ { t_i } { \sqrt { \left[ { { x } '(t) }\right]^2+\left[ { { y } '(t) }\right]^2+\left[ { { z } '(t) }\right]^2 } \cdot dt } $. По теореме о среднем, существует точка $\bar { t } _i $ такая, что

$\Delta l_i = { \sqrt { \left[ { { x } '(t) }\right]^2+\left[ { { y } '(t) }\right]^2+\left[ { { z } '(t) }\right]^2 } } \cdot \Delta t_i $, где $\Delta t_i = t_i - t_ { i-1 } $

Выберем точки $M_i $, получающиеся при этом значении параметра: $M_i (x_i ,y_i ,z_i )=M_i (x(\bar { t } _i ),y(\bar { t } _i ),z(\bar { t } _i ))$.

Тогда интегральная сумма для криволинейного интеграла $\sum\limits_ { i=1 } ^n { f(x_i ,y_i ,z_i )\cdot \Delta l_i } $ будет равна интегральной сумме для определенного интеграла $\sum\limits_ { i=1 } ^n { f(x(\bar { t } _i ),y(\bar { t } _i ),z(\bar { t } _i ))\cdot \sqrt { \left[ { { x } '(\bar { t } _i ) }\right]^2+\left[ { { y } '(\bar { t } _i ) }\right]^2+\left[ { { z } '(\bar { t } _i ) }\right]^2 } \cdot \Delta t_i } $.

Так как $\Delta l_i \to 0\Leftrightarrow \Delta t_i \to 0$, то, переходя к пределу при $\mathop { \max } \limits_ { i=1,2,\ldots ,n } \Delta l_i \to 0,\;\mbox { или, } \;\mbox { что } \;\mbox { тоже } \;\mbox { самое } ,\;\mathop { \max } \limits_ { i=1,2,\ldots ,n } \Delta t_i \to 0$ в равенстве $\sum\limits_ { i=1 } ^n { f(x_i ,y_i ,z_i )\cdot \Delta l_i } =\sum\limits_ { i=1 } ^n { f(x(\bar { t } _i ),y(\bar { t } _i ),z(\bar { t } _i ))\cdot \sqrt { \left[ { { x } '(\bar { t } _i ) }\right]^2+\left[ { { y } '(\bar { t } _i ) }\right]^2+\left[ { { z } '(\bar { t } _i ) }\right]^2 } \cdot \Delta t_i } $, получим

$ \int\limits_L { f(x,y,z)\cdot dl } =\int\limits_ { t_0 } ^ { t_k } { f(x(t),y(t),z(t))\cdot \sqrt { \left[ { { x } '(t) }\right]^2+\left[ { { y } '(t) }\right]^2+\left[ { { z } '(t) }\right]^2 } \cdot dt } . $

Таким образом, вычисление криволинейного интеграла первого рода сводится к вычислению определённого интеграла по параметру. Если кривая задана параметрически, то этот переход не вызывает трудностей; если дано качественное словесное описание кривой, то основной трудностью может быть введение параметра на кривой. Ещё раз подчеркнём, что интегрирование всегда ведётся в сторону возрастания параметра.

Примеры:

Пример 1

Вычислить $\int\limits_L { (x+y+z)dl } $, где $L$ - один виток спирали $L:\left[{ \begin{array} { l } x=R\cos t, \\ y=R\sin t, \\ z=at;\;0\leqslant t\leqslant 2\pi . \\ \end{array} }\right.$

Решение:

Здесь переход к определённому интегралу проблем не вызывает: находим $ { x } '(t)=-R\sin t,\; { y } '(t)=R\cos t,\; { z } '(t)=a,\;\sqrt { ( { x } '(t))^2+( { y } '(t))^2+( { z } '(t))^2 } =\sqrt { R^2+a^2 } $ , и $\int\limits_L { (x+y+z)dl } =\int\limits_0^ { 2\pi } { (R\cos t+R\sin t+at)\sqrt { R^2+a^2 } dt } =2\pi ^2a\sqrt { R^2+a^2 } $.

Пример 2

Вычислить тот же интеграл по отрезку прямой, соединяющей точки $A(1,2,3)$ и $B(-3,3,-8)$.

Решение:

Здесь прямого параметрического задания кривой нет, поэтому на $AB$ необходимо ввести параметр. Параметрические уравнения прямой имеют вид $\left[{ \begin{array} { l } x=x_0 +mt, \\ y=y_0 +nt, \\ z=z_0 +pt, \\ \end{array} }\right.$ где $\vec { a } \left[{ m,n,p }\right]$ - направляющий вектор, $(x_0 ,y_0 ,z_0 )$ - точка прямой.

В качестве точки берем точку $A(1,2,3)$, в качестве направляющего вектора - вектор $\mathop { AB } \limits^\to \left[{ -4,1,-11 }\right]$: $\left[{ \begin{array} { l } x=1-4t, \\ y=2+t, \\ z=3-11t, \\ \end{array} }\right.\Rightarrow dl=\sqrt { 16+1+121 } dt=\sqrt { 138 } dt$.

Легко видеть, что точка $A(1,2,3)$ соответствует значению $t=0$, точка $B(-3,3,-8)$ - значению $t=1$, поэтому $\int\limits_ { AB } { (x+y+z)dl } =\int\limits_0^1 { \left[ { (1-4t)+(2+t)+(3-11t) }\right] } \sqrt { 138 } dt=\sqrt { 138 } \int\limits_0^1 { (6-14t) } dt=-\sqrt { 138 } $.

Пример 3

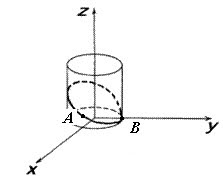
Найти $\int\limits_ { AB } { xyd\ell } $, где $\mathop { AB } \limits^\cup $ - часть сечения цилиндра $x^2+y^2=4$ плоскостью $\mathbf { \textit { z } } =\mathbf { \textit { x } } +1$, лежащая в первом октанте.

Решение:

Параметрические уравнения окружности - направляющей цилиндра имеют вид $\mathbf { \textit { x } } =2cos\varphi, \mathbf { \textit { y } } =2sin\varphi $, и так как $\mathbf { \textit { z=x } } +1$, то $\mathbf { \textit { z } } = 2cos\varphi +1$.

Итак,

$L=\mathop { AB } \limits^\cup :\left[{ \begin{array} { l } x=2\cos \varphi ,\;y=2\sin \varphi , \\ z=2\cos \varphi +1,\quad 0\leqslant \varphi \leqslant \pi /2; \\ \end{array} }\right.$ поэтому

$ \int\limits_ { AB } { xydl } = 8\int\limits_0^ { \pi/2 } { \cos \varphi \sin \varphi \sqrt { \sin ^2\varphi +\cos ^2\varphi +\sin ^2\varphi \, } } d\varphi = \frac { 8 } { 2 } \int\limits_0^ { \pi / 2 } { \sqrt { 1+\sin ^2\varphi } } d\sin ^2\varphi = \frac { 8 } { 3 } \left. { (1+\sin ^2\varphi )^ { 3 / 2 } }\right| _0^ { \pi / 2 } = 8\cdot \frac { 2\sqrt 2 -1 } { 3 } $