Условия независимости криволинейного интеграла от пути интегрирования

В этом разделе будет дан ответ на вопрос: при каких условиях криволинейный интеграл второго рода $\int\limits_ { \mathop { AB } \limits^\cup } { Pdx+Qdy } $ не зависит от формы пути, соединяющего точки $\mathbf { \textit { A } } $ и $\mathbf { \textit { B } } $, а определяется только этими точками?

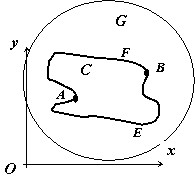
Будем предполагать, что в некоторой односвязной области $G$ на плоскости заданы непрерывно дифференцируемые функции $P(x,y)$ и $Q(x,y)$, и все рассматриваемые точки, контуры и области принадлежат этой области.

Теорема 1

Для того, чтобы интеграл $\int\limits_ { \mathop { AB } \limits^\cup } { Pdx+Qdy } $ не зависел от формы пути, соединяющего точки $\mathbf { \textit { A } } $ и $\mathbf { \textit { B } } $, необходимо и достаточно, чтобы интеграл по любому замкнутому контуру был равен нулю.

Доказательство

Необходимость . Пусть $C=\mathop { AEBFA } \limits^\cup $ - произвольный замкнутый контур, лежащий в области $G$, $\mathbf { \textit { A } } $ и $\mathbf { \textit { B } } $ - произвольные точки этого контура.

Так как, по условию, $\int\limits_ { \mathop { AEB } \limits^\cup } { Pdx+Qdy } =\int\limits_ { \mathop { AFB } \limits^\cup } { Pdx+Qdy } $, то $\int\limits_ { \mathop { AEB } \limits^\cup } { Pdx+Qdy } = -\int\limits_ { \mathop { BFA } \limits^\cup } { Pdx+Qdy } \Rightarrow \int\limits_ { \mathop { AEB } \limits^\cup } { Pdx+Qdy } +\int\limits_ { \mathop { BFA } \limits^\cup } { Pdx+Qdy } =0\Rightarrow \oint\limits_С { Pdx+Qdy } =0$.

Достаточность . Пусть для любого контура $C\subset G$ выполняется $\oint\limits_C { Pdx+Qdy } =0$. Пусть $\forall A\in G$, $\forall B\in G$ - произвольные точки, $\mathop { AEB } \limits^\cup $ и $\mathop { AFB } \limits^\cup $ - две различных кривых, соединяющих эти точки. $\mathop { AEBFA } \limits^\cup $ - замкнутый контур, поэтому $\oint\limits_ { \mathop { AEBFA } \limits^\cup } { Pdx+Qdy } =0\Rightarrow \oint\limits_ { \mathop { AEB } \limits^\cup } { Pdx+Qdy } + \quad +\oint\limits_ { \mathop { BFA } \limits^\cup } { Pdx+Qdy } =0\Rightarrow \quad \oint\limits_ { \mathop { AEB } \limits^\cup } { Pdx+Qdy } -\oint\limits_ { \mathop { AFB } \limits^\cup } { Pdx+Qdy } =0\Rightarrow \\ \int\limits_ { \mathop { AEB } \limits^\cup } { Pdx+Qdy } =\int\limits_ { \mathop { AFB } \limits^\cup } { Pdx+Qdy } $,

что и требовалось доказать.

Теорема 2

Для того, чтобы интеграл $\oint\limits_C { Pdx+Qdy } $ по любому контуру $\mathbf { \textit { C } } $ был равен нулю, необходимо и достаточно, чтобы функции $P, Q$ и их частные производные были непрерывны, и выполнялось условие $\frac { \partial Q } { \partial x } =\frac { \partial P } { \partial y } $.

Доказательство

Необходимость . От противного. Пусть для $\forall C\subset G$ выполняется $\oint\limits_C { Pdx+Qdy } =0$, но существует точка $M_0 \in G$ такая, что $\left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)(M_0 )\ne 0$.

Предположим для определённости, что $\left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)(M_0 )=s>0$. Так как разность $\frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } $ непрерывна, существует окрестность точки $M_0 $ такая, что $\left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)>s/2$.

Выберем контур $\mathbf { \textit { C } } $, целиком лежащий в этой окрестности. Если $\mathbf { \textit { D } } $ - область ограниченная этим контуром, то, по формуле Грина, $\oint\limits_С { P(x,y)dx+Q(x,y)dy=\iint\limits_D { \left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)dxdy } } $.

Но, по теореме об интегрировании неравенств, $\iint\limits_D { \left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)dxdy } >\frac { s } { 2 } \cdot S(D)>0$ { $S(D)$ - площадь области $\mathbf { \textit { D } } $ } , т.е. $\oint\limits_C { Pdx+Qdy } >0$, что противоречит условиям теоремы. Следовательно, в любой точке $M_0 \in G$ выполняется условие $\frac { \partial Q } { \partial x } =\frac { \partial P } { \partial y } $.

Достаточность . Если в любой точке $M_0 \in G$ выполняется условие $\frac { \partial Q } { \partial x } =\frac { \partial P } { \partial y } $, то для любого контура $\mathbf { \textit { C } } $

$\oint\limits_C { P(x,y)dx+Q(x,y)dy=\iint\limits_D { \left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)dxdy } } =0$ { $\mathbf { \textit { D } } $ - область ограниченная контуром $\mathbf { \textit { C } } $ } .

Таким образом, для того, чтобы криволинейный интеграл $\int\limits_ { \mathop { AB } \limits^\cup } { Pdx+Qdy } $ не зависел от формы пути, соединяющего начальную и конечную точки { или, что то же самое, интеграл по любому замкнутому контуру был равен нулю } , требуется выполнение двух условий:

1. Контур и ограниченная им область лежат в некоторой односвязной области, в которой
2. $P, Q$ и их частные производные непрерывны и $\frac { \partial Q } { \partial x } =\frac { \partial P } { \partial y } $.

Отметим существенность первого условия. Так, для интеграла $\int\limits_ { \mathop { AB } \limits^\cup } { \frac { ydx-xdy } { x^2+y^2 } } $ второе условие выполняется: $\frac { \partial Q } { \partial x } =\frac { \partial P } { \partial y } =\frac { x^2-y^2 } { \left( { x^2+y^2 }\right)^2 } $, в то же время интеграл по окружности радиуса $\mathbf { \textit { R } } $ не равен нулю: $\int\limits_ { x^2+y^2=R^2 } { \frac { ydx-xdy } { x^2+y^2 } } =\left| { \begin{array} { l } x=R\cos t,\;y=R\sin t \\ \quad 0\leqslant t\leqslant 2\pi \\ \end{array} }\right|=-\int\limits_0^ { 2\pi } { \left( { \sin ^2t+\cos ^2t }\right)dt=- } 2\pi $

Причина - функции $\mathbf { \textit { P } } $ и$\mathbf { \textit { Q } } $ непрерывны всюду, кроме начала координат; удаление точки из плоскости лишает её свойства односвязности.