Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах

Теорема о замене переменных в двойном интеграле

Пусть на плоскости $\mathbf { \textit { Ouv } } $ задана область $\mathbf { \textit { G } } $, и пусть отображение $\mathbf { \textit { F } } (\mathbf { \textit { M } } )=\mathbf { \textit { M } } $* преобразует эту область в область $\mathbf { \textit { D } } $ на плоскости $\mathbf { \textit { Oxy } } . $ Будем считать, что отображение $\mathbf { \textit { F } } $ задаётся функциями

$F:\left[ \begin{array} { l } x=x(u,v) \newline y=y(u,v) \newline \end{array} \right].$

Пусть:

1. $\mathbf { \textit { F } } $ взаимно однозначно отображает $\mathbf { \textit { G } } $ на $\mathbf { \textit { D } } $;
2. функции $\mathbf { \textit { x } } (\mathbf { \textit { u,v } } )\mathbf { \textit { , y } } (\mathbf { \textit { u,v } } )$ непрерывно дифференцируемы на $\mathbf { \textit { G } } $ { имеют непрерывные частные производные } ;

3. якобиан $J(u,v)=\frac { \partial (x,y) } { \partial (u,v) } =\left| { \begin{array} { l } \frac { \partial x } { \partial u } \quad \frac { \partial y } { \partial u } \newline \frac { \partial x } { \partial v } \quad \frac { \partial y } { \partial v } \newline \end{array} } \right|$ не обращается в нуль на $\mathbf { \textit { G } } .$

   $ { \frac { { \partial \left( { x,y }\right) } } { { \partial \left( { u,v }\right) } } } = { \left| { \begin{array} { * { 20 } { c } } { \frac { { \partial x } } { { \partial u } } } & { \frac { { \partial x } } { { \partial v } } } \\ { \frac { { \partial y } } { { \partial u } } } & { \frac { { \partial y } } { { \partial v } } } \end{array} }\right| } = { \left| { \begin{array} { * { 20 } { c } } { \frac { { \partial \left( { u\cos v }\right) } } { { \partial u } } } & { \frac { { \partial \left( { u\cos v }\right) } } { { \partial v } } } \\ { \frac { { \partial \left( { u\sin v }\right) } } { { \partial u } } } & { \frac { { \partial \left( { u\sin v }\right) } } { { \partial v } } } \end{array} }\right| } = { \left| { \begin{array} { * { 20 } { c } } { \cos v } & { - u\sin v } \\ { \sin v } & { u\cos v } \end{array} }\right| } = { \cos v \cdot u\cos v - \left( { - u\sin v }\right) \cdot \sin v } = { u\, { \cos ^2 } v + u\, { \sin ^2 } v } = \\ = { u\left( { { { \cos } ^2 } v + { { \sin } ^2 } v }\right) = u. } $

   Докажем, что в этих предположениях $\iint\limits_D { f(x,y)dxdy=\iint\limits_G { f(x(u,v),y(u,v))\cdot \left| { J(u,v) }\right|\cdot dudv } } $.

Док-во:

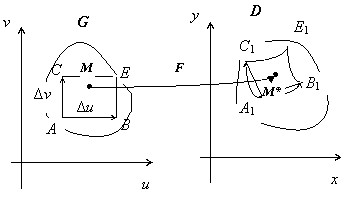
Рассмотрим, как связаны между собой площадь параллелограмма $\mathbf { \textit { АВСЕ } } $ со сторонами $\Delta u,\Delta v $в области $\mathbf { \textit { G } } $ и площадь его образа при преобразовании $\mathbf { \textit { F } } \textbf { - } $криволинейного параллелограмма $\mathbf { \textit { A } } _ { 1 } \mathbf { \textit { B } } _ { 1 } \mathbf { \textit { C } } _ { 1 } \mathbf { \textit { E } } _ { 1 } $ в области $\mathbf { \textit { D } } .$ С точностью до бесконечно малых высших порядков по сравнению с $\Delta u,\Delta v$, площадь криволинейного параллелограмма $\mathbf { \textit { A } } _ { 1 } \mathbf { \textit { B } } _ { 1 } \mathbf { \textit { C } } _ { 1 } \mathbf { \textit { E } } _ { 1 } $ равна площади обычного параллелограмма, построенного на векторах $\overline { A_1 B_1 } $ и $\overline { A_1 C_1 } $. Пусть точка $А$ имеет координаты $\mathbf { \textit { u,v } } $, тогда точка $\mathbf { \textit { А } } _ { 1 } $ будет иметь координаты $\mathbf { \textit { x } } (\mathbf { \textit { u,v } } ),\mathbf { \textit { y } } (\mathbf { \textit { u,v } } ))$, т.е. $A(u,v)\to A_1 (x(u,v),y(u,v))$. Для других точек: $B(u+\Delta u,v)\to B_1 (x(u+\Delta u,v),y(u+\Delta u,v))= \quad B_1 (x(u,v)+\frac { \partial x } { \partial u } (u,v)\Delta u+\alpha _1 (\Delta u)\Delta u,y(u,v)+\frac { \partial y } { \partial u } (u,v)\Delta u+\alpha _2 (\Delta u)\Delta u)$ { по формуле приращения дифференцируемой функции } . Аналогично $C(u,v+\Delta v)\to C_1 (x(u,v+\Delta v),y(u,v+\Delta v))=$

$C_1 (x(u,v)+\frac { \partial x } { \partial v } (u,v)\Delta v+\alpha _3 (\Delta v)\Delta v,y(u,v)+\frac { \partial y } { \partial v } (u,v)\Delta v+\alpha _4 (\Delta v)\Delta v),$ где $\alpha _i \to 0\;(i=1,2,3,4)$ при $\Delta u,\Delta v\to 0$.

Пренебрежём членами порядка малости выше первого по сравнению с $\Delta u,\Delta v$. Тогда $ \overline { AB } [\Delta u,0]\to \overline { A_1 B_1 } \left[ { \frac { \partial x } { \partial u } (u,v),\frac { \partial y } { \partial u } (u,v) \left. { \begin{array} { l } \newline \newline \end{array} }\right] ; } \right.\overline { AC } [0,\Delta v]\to \overline { A_1 C_1 } \left[ { \frac { \partial x } { \partial v } (u,v),\frac { \partial y } { \partial v } (u,v)\left. { \begin{array} { l } \newline \newline \end{array} } \right] } \right. $

Пусть теперь $\textbf { i,j,k } $ - базисные орты пространства, в котором лежит плоскость $\mathbf { \textit { Oxy } } $. Как известно, площадь параллелограмма, построенного на векторах $\overline { A_1 B_1 } $ и $\overline { A_1 C_1 } $, равна модулю векторного произведения этих векторов { проекции на орт $\textbf { k } $равны нулю } : $$ S_ { A_1 B_1 C_1 E_1 } =\left| { \left[ { \overline { A_1 B_1 } \ast \overline { A_1 C_1 } }\right] }\right|=\left| { \left| { \begin{array} { l } { \rm { \bf i } } \quad \;\;\;\;\;\; { \rm { \bf j } } \quad \;\;\;\; { \rm { \bf k } } \newline \frac { \partial x } { \partial u } \Delta u\;\;\frac { \partial y } { \partial u } \Delta u\;\;0 \newline \frac { \partial x } { \partial v } \Delta v\;\;\frac { \partial y } { \partial v } \Delta v\;\;0 \newline \end{array} }\right| }\right|=\left| { \rm { \bf k } }\right|\left| { \left| { \begin{array} { l } \frac { \partial x } { \partial u } \Delta u\;\;\frac { \partial y } { \partial u } \Delta u \newline \frac { \partial x } { \partial v } \Delta v\;\;\frac { \partial y } { \partial v } \Delta v \newline \end{array} }\right| }\right|=\left| { \left| { \begin{array} { l } \frac { \partial x } { \partial u } \;\;\frac { \partial y } { \partial u } \newline \frac { \partial x } { \partial v } \;\;\frac { \partial y } { \partial v } \newline \end{array} }\right| }\right|\left| { \Delta u\Delta v }\right|=\left| { J(u,v) }\right|S_ { ABCE } . $$

Мы доказали замечательную вещь. Если вокруг точки $M\in G$ взять маленькую область, то после преобразования $\mathbf { \textit { F } } $ площадь этой области меняется в $\vert \quad \mathbf { \textit { J } } (\mathbf { \textit { M } } ) \quad \vert $ раз.

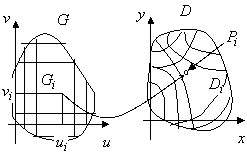
2. Перейдём к доказательству основной формулы. Разобьём $\mathbf { \textit { G } } $ прямыми, параллельными осям координат, на области $\mathbf { \textit { G } } _ { 1 } $, $\mathbf { \textit { G } } _ { 2 } , { \ldots } , \mathbf { \textit { G } } _ { n } $. Образы этих линий дадут разбиение $\mathbf { \textit { D } } $ на области $\mathbf { \textit { D } } _ { 1 } $, $\mathbf { \textit { D } } _ { 2 } , { \ldots } , \mathbf { \textit { D } } _ { n } $. Для этого разбиения составим интегральную cумму $\sum\limits_ { i=1 } ^n { f(P_i )S(D_i )= } \sum\limits_ { i=1 } ^n { f(x(u_i ,v_i ),y(u_i ,v_i ))\left| J \right|S(G_i ) } $. Устремим $\mathop { \max } \limits_ { i=1,2,...,n } diam(G_i )\to 0$; тогда и $\mathop { \max } \limits_ { i=1,2,...,n } diam(D_i )\to 0$. И слева, и справа интегральные суммы записаны для непрерывных функций, следовательно,и слева, и справа существуют пределы - двойные интегралы, и они равны: $\iint\limits_D { f(x,y)dxdy=\iint\limits_G { f(u,v)\cdot \left| { J(u,v) }\right|\cdot dudv } } $, что и требовалось доказать.

   Двойной интеграл в полярных координатах

Нам придётся применять эту формулу, в основном, для перехода к полярным координатам. Роль переменных $\mathbf { \textit { u } } $ и $\mathbf { \textit { v } } $ будут играть $\mathbf { \textit { r } } $ и $\phi $. Как известно, $x=r\cos \varphi ,y=r\sin \varphi $. Вычислим якобиан: $J=\left| { \left| { \begin{array} { l } \cos \varphi \quad \;\;\;\;\sin \varphi \newline -r\sin \varphi \;\;r\cos \varphi \newline \end{array} }\right| }\right|=\vert r\vert =r$, следовательно, $\iint\limits_ { D(x,y) } { f(x,y)dxdy } =\iint\limits_ { D(r,\phi ) } { f(r\cos \varphi ,r\sin \varphi )rdrd\varphi } $. Двойной интеграл в координатах $\mathbf { \textit { r } } ,\phi $ вычисляется также как и в координатах $\mathbf { \textit { x } } ,\mathbf { \textit { y } } , $переходом к двухкратному, при этом внешний обычно берут по $\varphi $. Если область $\mathbf { \textit { D } } $ описывается как $D:\left[ { \begin{array} { l } \varphi _0 \leqslant \varphi \leqslant \varphi _k \newline r_1 (\varphi )\leqslant r\leqslant r_2 (\varphi ) \newline \end{array} } \right]$, то $\iint\limits_ { D(r,\varphi ) } { f(r\cos \varphi ,r\sin \varphi )rdrd\varphi } =\int\limits_ { \varphi _0 } ^ { \varphi _k } { d\varphi \int\limits_ { r_1 (\varphi ) } ^ { r_2 (\varphi ) } { f(r\cos \varphi ,r\sin \varphi )rdr } } $. Естественно, если $r_1 (\varphi ),r_2 (\varphi )$ - кусочные функции, то внешний интеграл разбивается на несколько слагаемых. Однозначно дать рецепт, когда имеет смысл переходить к полярным координатам, нельзя, это дело опыта. Можно пробовать перейти к $\mathbf { \textit { r } } ,\phi $, если либо $\mathbf { \textit { f } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } )$, либо кривые, ограничивающие область интегрирования, либо и то, и другое вместе, зависят от комбинации $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } =\mathbf { \textit { r } } ^ { 2 } $. Если $f(x,y)=f\left( { \frac { x^2 } { a^2 } +\frac { y^2 } { b^2 } }\right)$ и/или область $\mathbf { \textit { D } } $ ограничивается эллипсом $\frac { x^2 } { a^2 } +\frac { y^2 } { b^2 } =1$, полезны обобщённые полярные координаты $x=ar\cos \varphi ,y=br\sin \varphi $. Каков якобиан этого преобразования?