Вычисление площади поверхности

Пример 1

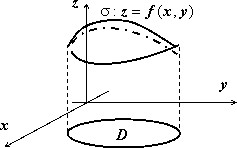
Пусть в пространстве задана кусочно-гладкая поверхность $\sigma $, однозначно проектирующаяся в область $\mathbf { \textit { D } } $ на плоскости $\mathbf { \textit { Оху } } $. Пусть эта поверхность задаётся уравнением $\sigma :\;z=f(x,y),\;(x,y)\in D$. Тогда площадь этой поверхности выражается формулой

$ s(\sigma )=\iint\limits_D { \sqrt { 1+\left( { \frac { \partial f } { \partial x } }\right)^2+\left( { \frac { \partial f } { \partial y } }\right)^2 } dxdy } . $

Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } $ = 2$\mathbf { \textit { ax } } $ из сферы $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } $ = 4$\mathbf { \textit { a } } ^ { 2 } $ .

Решение:

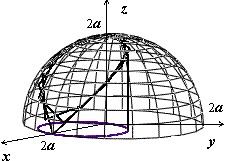
На рисунке изображён верхний из этих лепестков. Уравнение поверхности $z=\sqrt { 4a^2-x^2-y^2 } ,$ вычисляем производные $\frac { \partial z } { \partial x } =-\frac { x } { \sqrt { 4a^2-x^2-y^2 } } , \quad \frac { \partial z } { \partial y } =-\frac { y } { \sqrt { 4a^2-x^2-y^2 } } ,$ и $s(\sigma )=\iint\limits_D { \sqrt { 1+\frac { x^2+y^2 } { 4a^2-x^2-y^2 } dxdy } } =2a\iint\limits_D { \frac { dxdy } { \sqrt { 4a^2-x^2-y^2 } } } $.

Область $\mathbf { \textit { D } } $ - сдвинутый на $\mathbf { \textit { а } } $ единиц по оси $\mathbf { \textit { Ох } } $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $\mathbf { \textit { Оху } } $ и $\mathbf { \textit { Охz } } $:

$s(\sigma )=4\cdot 2a\iint\limits_ { D_ { r,\varphi } } { \frac { rdrd\varphi } { \sqrt { 4a^2-r^2 } } } =8a\int\limits_0^ { \pi /2 } { d\varphi \int\limits_0^ { 2a\cos \varphi } { \left( { 4a^2-r^2 }\right)^ { -1/2 } rdr } } =-8a\int\limits_0^ { \pi /2 } { d\varphi \left. { \left( { 4a^2-r^2 }\right)^ { 1/2 } }\right|_0^ { 2a\cos \varphi } } = \\ =8a\int\limits_0^ { \pi /2 } { \left[ { 2a-2a\sqrt { 1-\cos ^2\varphi } }\right]d\varphi } =16a^2\left. { \left( { \varphi +\cos \varphi }\right) }\right|_0^ { \pi /2 } =16a^2\left( { \pi /2-1 }\right)$.

Пример 2

Вычислить площадь cферы радиуса (a.)

Решение:

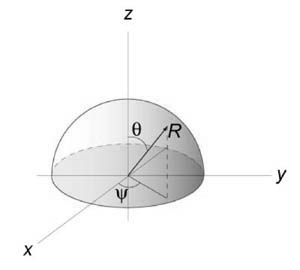
Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ { { x^2 } + { y^2 } + { z^2 } = { a^2 } } \;\; { \text { или } \;\;z = \sqrt { { a^2 } - { x^2 } - { y^2 } } . } $

Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ { S_ { \large\frac { 1 } { 2 } \normalsize } } = \iint\limits_R { \sqrt { 1 + { { \left( { \frac { { \partial z } } { { \partial x } } }\right) } ^2 } + { { \left( { \frac { { \partial z } } { { \partial y } } }\right) } ^2 } } dxdy } .$

Найдем частные производные. $ { \frac { { \partial z } } { { \partial x } } } = { \frac { \partial } { { \partial x } } \sqrt { { a^2 } - { x^2 } - { y^2 } } } = { \frac { { - { 2 } x } } { { { 2 } \sqrt { { a^2 } - { x^2 } - { y^2 } } } } } = { - \frac { x } { z } , } $ $ { \frac { { \partial z } } { { \partial y } } } = { \frac { \partial } { { \partial y } } \sqrt { { a^2 } - { x^2 } - { y^2 } } } = { \frac { { - { 2 } y } } { { { 2 } \sqrt { { a^2 } - { x^2 } - { y^2 } } } } } = { - \frac { y } { z } . } $

Подставляя найденные производные, получаем $ { { S_ { \large\frac { 1 } { 2 } \normalsize } } = \iint\limits_R { \sqrt { 1 + { { \left( { \frac { { \partial z } } { { \partial x } } }\right) } ^2 } + { { \left( { \frac { { \partial z } } { { \partial y } } }\right) } ^2 } } dxdy } } = { \iint\limits_R { \sqrt { 1 + \frac { { { x^2 } } } { { { z^2 } } } + \frac { { { y^2 } } } { { { z^2 } } } } dxdy } } = { \iint\limits_R { \sqrt { \frac { { { z^2 } + { x^2 } + { y^2 } } } { { { z^2 } } } } dxdy } } = { \iint\limits_R { \frac { a } { z } dxdy } . } $

Преобразуем двойной интеграл в полярные координаты. $ { { S_ { \large\frac { 1 } { 2 } \normalsize } } = \iint\limits_R { \frac { a } { z } dxdy } } = { \int\limits_0^ { 2\pi } { \int\limits_0^a { \frac { a } { { \sqrt { { a^2 } - { r^2 } } } } rdrd\theta } } } = { a\int\limits_0^ { 2\pi } { d\theta } \int\limits_0^a { \frac { { rdr } } { { \sqrt { { a^2 } - { r^2 } } } } } } = { - 2\pi a\int\limits_0^a { \frac { { d\left( { { a^2 } - { r^2 } }\right) } } { { 2\sqrt { { a^2 } - { r^2 } } } } } } = { - 2\pi a\left. { \left( { \sqrt { { a^2 } - { r^2 } } }\right) }\right|_ { r = 0 } ^a } = { - 2\pi a\left( { 0 - a }\right) = 2\pi { a^2 } . } $

Площадь поверхности полной сферы, соответственно, равна $S = 2 { S_ { \large\frac { 1 } { 2 } \normalsize } } = 4\pi { a^2 } .$