Вычисление площадей плоских областей
В соответствии с свойством Интеграл от единичной функции $s(D)=\iint\limits_D { dxdy } $.
Пример 1
Найти площадь области , лежащей внутри кривых $\left( { x^2+y^2 }\right)^2=a^2\left( { x^2-y^2 }\right),\;x^2+y^2=a\sqrt 2 \left( { \sqrt { x^2+y^2 } -x }\right)$.
Решение:
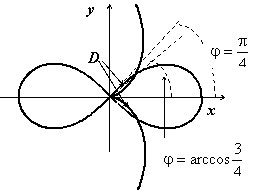
Построить эти кривые можно только в полярных координатах; первое уравнение приводится к виду $r=a\sqrt { \cos 2\varphi } $, это - лемниската Бернулли; второе - к виду $r=a\sqrt 2 \left( { 1-\cos \varphi }\right)$ - это кардиоида. Решая уравнение $a\sqrt { \cos 2\varphi } =a\sqrt 2 \left( { 1-\cos \varphi }\right)$, находим, что точка их пересечения лежит на луче $\varphi =\arccos (3/4)$.$\mathbf { \textit { D } } $состоит из двух лунок одинаковой площади; вычислим площадь верхней. При $0\leqslant \varphi \leqslant \arccos (3/4)$эта лунка ограничена кардиоидой; при $\arccos (3/4)\leqslant \varphi \leqslant \pi /4$ - лемнискатой, поэтому $s(D)=\iint\limits_D { dxdy } =\iint\limits_ { D_ { r,\varphi } } { rdrd\varphi } =\int\limits_0^ { \arccos (3/4) } { d\varphi \int\limits_0^ { a\sqrt 2 (1-\cos \varphi ) } { rdr } } +\int\limits_ { \arccos (3/4) } ^ { \pi /4 } { d\varphi \int\limits_0^ { a\sqrt { 2\cos 2\varphi } } { rdr } } = \\ = \int\limits_0^ { \arccos (3/4) } { d\varphi \cdot \left. { \frac { r^2 } { 2 } }\right|_0^ { a\sqrt 2 (1-\cos \varphi ) } } +\int\limits_ { \arccos (3/4) } ^ { \pi /4 } { d\varphi \cdot \left. { \frac { r^2 } { 2 } }\right|_0^ { a\sqrt { 2\cos 2\varphi } } } = \\ = a^2\int\limits_0^ { \arccos (3/4) } { (1-\cos \varphi )^2d\varphi } +a^2\int\limits_ { \arccos (3/4) } ^ { \pi /4 } { \cos 2\varphi d\varphi } = a^2\left. { \left( { \frac { 3 } { 2 } \varphi -2\sin \varphi +\frac { \sin 2\varphi } { 4 } }\right) }\right|_0^ { \arccos (3/4) } +\frac { a^2 } { 2 } \left. { \sin 2\varphi }\right|_ { \arccos (3/4) } ^ { \pi /4 } = \\ =a^2\left( { \frac { 3 } { 2 } \arccos (3/4)-2\sin \arccos (3/4)+\frac { \sin (2\arccos (3/4)) } { 4 } }\right)+\frac { a^2 } { 2 } \left( { 1-\sin (2\arccos (3/4)) }\right) = \\ = a^2\left( { \frac { 3 } { 2 } \arccos (3/4)-2\sqrt { 1-(3/4)^2 } +\frac { 1 } { 4 } \cdot 2\cdot \sqrt { 1-(3/4)^2 } \cdot \frac { 3 } { 4 } }\right)+\frac { a^2 } { 2 } \left( { 1-2\cdot \sqrt { 1-(3/4)^2 } \cdot \frac { 3 } { 4 } }\right)= \\ =\frac { a^2 } { 2 } \left( { 1-\frac { 19\sqrt 7 } { 16 } }\right)+\frac { 3 } { 2 } a^2\arccos (3/4) $
Пример 2
Вычислить площадь области (R,) ограниченной линиями ( { y^2 } = { a^2 } - ax,) (y = a + x.)
Решение:
Сначала определим точки пересечения двух заданных линий. $ { \left[ \begin{array} { l } { y^2 } = { a^2 } - ax\\ y = a + x \end{array}\right., } \;\; { \Rightarrow { \left( { a + x }\right)^2 } = { a^2 } - ax, } \;\; { \Rightarrow { a^2 } + 2ax + { x^2 } = { a^2 } - ax, } \;\; { \Rightarrow { x^2 } + 3ax = 0, } \;\; { \Rightarrow x\left( { x + 3a }\right) = 0, } \;\; { \Rightarrow { x_ { 1,2 } } = 0;\; - 3a. } $
Площадь области типа (I)
(A = \large\int\limits_a^b\normalsize { \large\int\limits_ { g\left( x \right) } ^ { f\left( x \right) } \normalsize { dydx } } ) 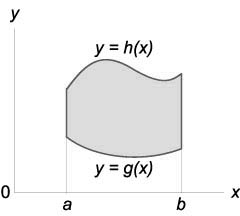
Площадь области типа (II)
(A = \large\int\limits_c^d\normalsize { \large\int\limits_ { p\left( y \right) } ^ { q\left( y \right) } \normalsize { dxdy } } ) 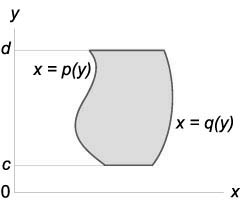
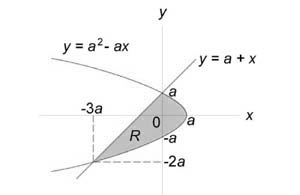
Следовательно, координаты точек пересечения равны $ { x_1 } = 0,\;\; { y_1 } = a + 0 = a,$ $ { x_2 } = - 3a,\;\; { y_2 } = a - 3a = - 2a.$ Область (R) представлена на рисунке.
Будем рассматривать ее как область типа (II.) Для вычисления площади преобразуем уравнения границ: $ { { y^2 } = { a^2 } - ax, } \;\; { \Rightarrow ax = { a^2 } - { y^2 } , } \;\; { \Rightarrow x = a - \frac { { { y^2 } } } { a } , } $ $ { y = a + x, } \;\; { \Rightarrow x = y - a. } $ Получаем $ { A = \iint\limits_R { dxdy } } = { \int\limits_ { - 2a } ^a { \left[ { \int\limits_ { y - a } ^ { a - \frac { { { y^2 } } } { a } } { dx } }\right]dy } } = { \int\limits_ { - 2a } ^a { \left[ { \int\limits_ { y - a } ^ { a - \frac { { { y^2 } } } { a } } { dx } }\right]dy } } = { \int\limits_ { - 2a } ^a { \left[ { \left. x \right|_ { y - a } ^ { a - \frac { { { y^2 } } } { a } } }\right]dy } } = { \int\limits_ { - 2a } ^a { \left[ { a - \frac { { { y^2 } } } { a } - \left( { y - a }\right) }\right]dy } } = \\ = { \int\limits_ { - 2a } ^a { \left( { 2a - \frac { { { y^2 } } } { a } - y }\right)dy } } = { \left. { \left( { 2ay - \frac { { { y^3 } } } { { 3a } } - \frac { { { y^2 } } } { 2 } }\right) }\right|_ { - 2a } ^a } = { \left( { 2 { a^2 } - \frac { { { a^3 } } } { { 3a } } - \frac { { { a^2 } } } { 2 } }\right) - \left( { - 4 { a^2 } + \frac { { 8 { a^3 } } } { { 3a } } - \frac { { 4 { a^2 } } } { 2 } }\right) } = { \frac { { 9 { a^2 } } } { 2 } . } $
Пример 3
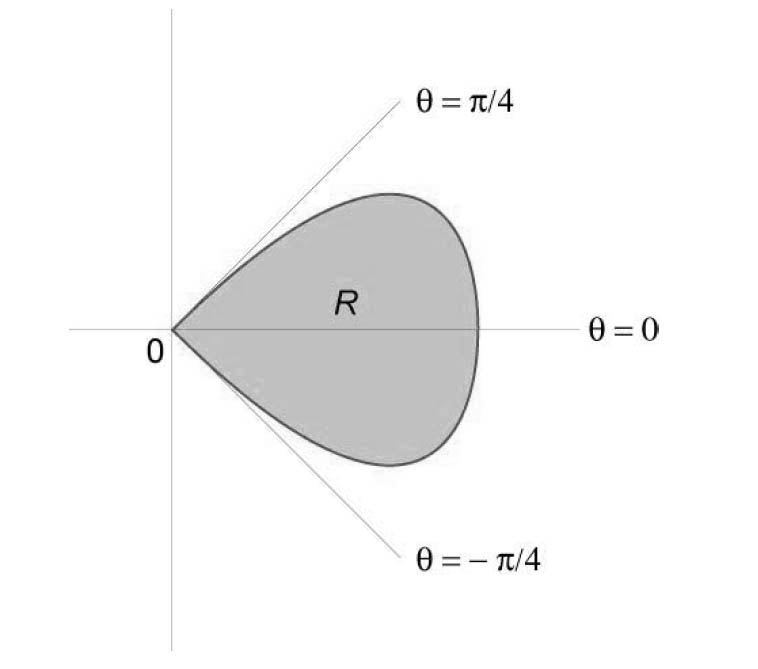
Найти площадь лепестка розы, заданной уравнением (r = \cos 2\theta.)
Решение:
Рассмотрим лепесток в секторе ( - \large\frac { \pi } { 4 } \normalsize \le \theta \le \large\frac { \pi } { 4 } \normalsize). Область интегрирования имеет вид (R = \left[{ \left( { r,\theta }\right)|\;0 \le r \le \cos 2\theta , - \large\frac { \pi } { 4 } \normalsize \le \theta \le \large\frac { \pi } { 4 } \normalsize }\right].)
Следовательно, площадь данной фигуры в полярных координатах равна $ { A = \iint\limits_R { rdrd\theta } } = { \int\limits_ { - \large\frac { \pi } { 4 } \normalsize } ^ { \large\frac { \pi } { 4 } \normalsize } { \left[ { \int\limits_0^ { \cos 2\theta } { rdr } }\right]d\theta } } = { \int\limits_ { - \large\frac { \pi } { 4 } \normalsize } ^ { \large\frac { \pi } { 4 } \normalsize } { \left[ { \left. { \left( { \frac { { { r^2 } } } { 2 } }\right) }\right|_0^ { \cos 2\theta } }\right]d\theta } } = { \frac { 1 } { 2 } \int\limits_ { - \large\frac { \pi } { 4 } \normalsize } ^ { \large\frac { \pi } { 4 } \normalsize } { { { \cos } ^2 } \left( { 2\theta }\right)d\theta } } = { \frac { 1 } { 2 } \int\limits_ { - \large\frac { \pi } { 4 } \normalsize } ^ { \large\frac { \pi } { 4 } \normalsize } { \frac { { 1 + \cos 4\theta } } { 2 } d\theta } } = \\ = { \frac { 1 } { 4 } \int\limits_ { - \large\frac { \pi } { 4 } \normalsize } ^ { \large\frac { \pi } { 4 } \normalsize } { \left( { 1 + \cos 4\theta }\right)d\theta } } = { \frac { 1 } { 4 } \left. { \left( { \theta + \frac { { \sin 4\theta } } { 4 } }\right) }\right|_ { - \large\frac { \pi } { 4 } \normalsize } ^ { \large\frac { \pi } { 4 } \normalsize } } = { \frac { 1 } { 4 } \left[ { \left( { \frac { \pi } { 4 } + \frac { { \sin \pi } } { 4 } }\right) - \left( { - \frac { \pi } { 4 } + \frac { { \sin \left( { - \pi }\right) } } { 4 } }\right) }\right] } = { \frac { \pi } { 8 } . } $
Далее:
Вычисление криволинейного интеграла первого рода. Примеры
Свойства двойного интеграла
Механические приложения тройного интеграла
Вычисление объёмов
Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному
Инвариантное определение дивергенции
Теорема о полныx системаx в Pk
Линейный интеграл и циркуляция векторного поля
Теорема о заведомо полныx системаx
Механические приложения двойного интеграла
Класс M. Теорема о замкнутости класса M
Вычисление криволинейного интеграла первого рода. Плоский случай
Замыкание. Свойства замыкания. Теорема о сведении к заведомо полной системе
Поверхностный интеграл второго рода и его свойства
Вычисление двойного интеграла
Огравление $\Rightarrow $
Комментарии ()