Вычисление объёмов

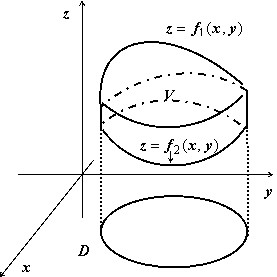
Объём тела, ограниченного сверху и снизу поверхностями $\mathbf { \textit { z } } =\mathbf { \textit { f } } _ { 1 } (\mathbf { \textit { x } } $,$\mathbf { \textit { y } } )$, $\mathbf { \textit { z } } =\mathbf { \textit { f } } _ { 2 } (\mathbf { \textit { x } } $,$\mathbf { \textit { y } } )$, $(x,y)\in D$, с боков - цилиндрической поверхностью с образующими, параллельными оси $\mathbf { \textit { Oz } } $, равен $v=\iint\limits_D { \left[ { f_1 (x,y)-f_2 (x,y) }\right]dxdy } $; эта формула очевидно следует из геометрического смысла двойного интеграла.

Основной вопрос, который надо решить - на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.

Пример 1

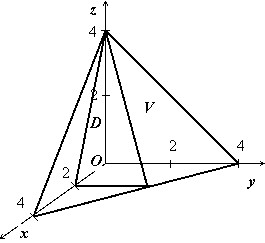
Найти объём тела $V:\left[{ \begin{array} { l } y=0,\;z=0, \\ x+y+z=4,\; \\ 2x+z=4. \\ \end{array} }\right.$

Решение:

Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $\mathbf { \textit { Oxz } } $:

$V:\left[{ \begin{array} { l } (x,z)\in D, \\ 0\leqslant y\leqslant 4-x-z. \\ \end{array} }\right.$

Область $\mathbf { \textit { D } } $ - треугольник, ограниченный прямыми $\mathbf { \textit { x } } $ = 0, $\mathbf { \textit { z } } $ = 0, 2$\mathbf { \textit { x } } +\mathbf { \textit { z } } $ = 4, поэтому

$V=\iint\limits_D { (4-x-z)dxdz } =\int\limits_0^2 { dx\int\limits_0^ { 4-2x } { (4-x-z)dz } } = \int\limits_0^2 { dx\left. { \left( { 4z-xz-z^2/2 }\right) }\right|_0^ { 4-2x } } = \int\limits_0^2 { \left[ { 16-8x-4x+2x^2-(4-2x)^2/2 }\right]dx } = \\ = \int\limits_0^2 { \left( { 8-4x }\right)dx } = \left. { \left( { 8x-2x^2 }\right) }\right|_0^2 =16-8=8$

Пример 2

Найти объём области, ограниченной поверхностями $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } =\mathbf { \textit { R } } ^ { 2 } $,

$(\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } )^ { 3 } =\mathbf { \textit { R } } ^ { 2 } (\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } )$.

Решение:

Первая поверхность - сфера, вторая - цилиндрическая - с образующими, параллельными оси $\mathbf { \textit { Oz } } $ { в уравнении нет $\mathbf { \textit { z } } $ в явной форме). Построить в плоскости $\mathbf { \textit { Oxy } } $ кривую шестого порядка, заданную уравнением $(\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } )^ { 3 } =\mathbf { \textit { R } } ^ { 2 } (\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } )$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей { чётные степени } и точка $\mathbf { \textit { О } } (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(\cos ^4\varphi +\sin ^4\varphi );r^2=R^2((\cos ^2\varphi +\sin ^2\varphi )^2-2\cos ^2\varphi \sin ^2\varphi )=R^2(1-\frac { \sin ^22\varphi } { 2 } )=$

$=R^2(1-\frac { 1-\cos 4\varphi } { 4 } )=R^2\frac { 3+\cos 4\varphi } { 4 } ;r=R\frac { \sqrt { 3+\cos 4\varphi } } { 2 } .$ Эту кривую построить уже можно. $r(\varphi )$ максимально, когда $\cos 4\varphi =1\;(\varphi =0,\frac { 2\pi } { 4 } =\frac { \pi } { 2 } ,\frac { 4\pi } { 4 } =\pi ,\frac { 6\pi } { 4 } =\frac { 3\pi } { 2 } )$, минимально, когда

$\cos 4\varphi =-1\;(\varphi =\frac { \pi } { 4 } ,\frac { 3\pi } { 4 } ,\frac { 5\pi } { 4 } ,\frac { 7\pi } { 4 } ),$ и гладко меняется между этими пределами { точка $\mathbf { \textit { О } } (0,0)$ не принадлежит этой кривой, где мы её потеряли? } .

Пользуясь симметрией, получаем $ V=16\iint\limits_D { \sqrt { R^2-x^2-y^2 } dxdy= } 16\iint\limits_D { \sqrt { R^2-r^2 } rdrd\varphi = } =16\int\limits_0^ { \frac { \pi } { 4 } } { d\varphi } \int\limits_0^ { R\frac { \sqrt { 3+\cos 4\varphi } } { 2 } } { \sqrt { R^2-r^2 } rdr } = $ $ =-8\int\limits_0^ { \frac { \pi } { 4 } } { d\varphi } \int\limits_0^ { R\frac { \sqrt { 3+\cos 4\varphi } } { 2 } } { \sqrt { R^2-r^2 } d(R^2-r^2) } =-8\frac { 2 } { 3 } \int\limits_0^ { \frac { \pi } { 4 } } { \left. { (R^2-r^2)^ { \frac { 3 } { 2 } } }\right|_0^ { R\frac { \sqrt { 3+\cos 4\varphi } } { 2 } } d\varphi } =-\frac { 16 } { 3 } R^3\int\limits_0^ { \frac { \pi } { 4 } } { \left. { \left[ { \left( { \frac { \sin ^22\varphi } { 2 } }\right)^ { \frac { 3 } { 2 } } -1 }\right] }\right|d\varphi } = $ и т.д.

Пример 3

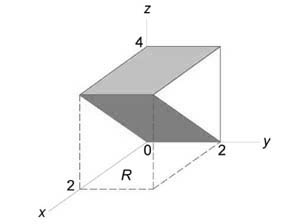
Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)

Решение:

Данное тело показано на рисунке.

Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 - x.) Тогда объем равен $ { V = \iint\limits_R { \left[ { \left( { 4 - x }\right) - x }\right]dxdy } } = { \int\limits_0^2 { \left[ { \int\limits_0^2 { \left( { 4 - 2x }\right)dy } }\right]dx } } = { \int\limits_0^2 { \left[ { \left. { \left( { 4y - 2xy }\right) }\right|_ { y = 0 } ^2 }\right]dx } } = { \int\limits_0^2 { \left( { 8 - 4x }\right)dx } } = { \left. { \left( { 8x - 2 { x^2 } }\right) }\right|_0^2 } = { 16 - 8 = 8. } $

Пример 4

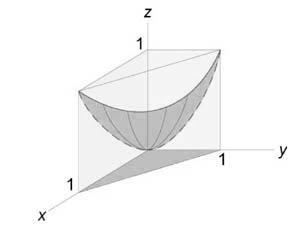
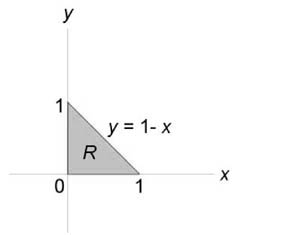
Описать тело, объем которого определяется интегралом (V = \int\limits_0^1 { dx } \int\limits_0^ { 1 - x } { \left( { { x^2 } + { y^2 } }\right)dy } .)

Решение:

Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 - x) ниже параболической поверхности (z = { x^2 } + { y^2 } .) Объем тела равен $ { V = \int\limits_0^1 { dx } \int\limits_0^ { 1 - x } { \left( { { x^2 } + { y^2 } }\right)dy } } = { \int\limits_0^1 { \left[ { \left. { \left( { { x^2 } y + \frac { { { y^3 } } } { 3 } }\right) }\right|_ { y = 0 } ^ { 1 - x } }\right]dx } } = { \int\limits_0^1 { \left[ { { x^2 } \left( { 1 - x }\right) + \frac { { { { \left( { 1 - x }\right) } ^3 } } } { 3 } }\right]dx } } = \\ = { \int\limits_0^1 { \left( { { x^2 } - { x^3 } + \frac { { 1 - 3x + 3 { x^2 } - { x^3 } } } { 3 } }\right)dx } } = { \int\limits_0^1 { \left( { 2 { x^2 } - \frac { { 4 { x^3 } } } { 3 } - x + \frac { 1 } { 3 } }\right)dx } } = { \left. { \left( { \frac { { 2 { x^3 } } } { 3 } - \frac { 4 } { 3 } \cdot \frac { { { x^4 } } } { 4 } - \frac { { { x^2 } } } { 2 } + \frac { x } { 3 } }\right) }\right|_0^1 } = { \frac { 2 } { 3 } - \frac { 1 } { 3 } - \frac { 1 } { 2 } + \frac { 1 } { 3 } = \frac { 1 } { 6 } . } $

Пример 5

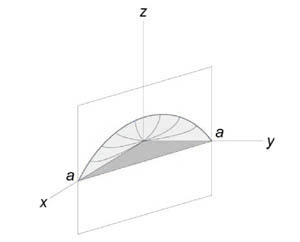
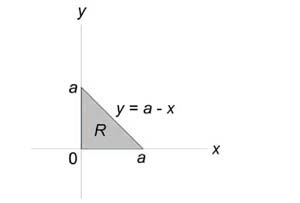
Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)

Решение:

Данное тело лежит над треугольником (R) в плоскости (Oxy) ниже поверхности (z = xy.) Объем тела равен $ { V = \iint\limits_R { xydxdy } } = { \int\limits_0^a { \left[ { \int\limits_0^ { a - x } { xydy } }\right]dx } } = { \int\limits_0^a { \left[ { \left. { \left( { \frac { { x { y^2 } } } { 2 } }\right) }\right|_ { y = 0 } ^ { a - x } }\right]dx } } = { \frac { 1 } { 2 } \int\limits_0^a { x { { \left( { a - x }\right) } ^2 } dx } } = { \frac { 1 } { 2 } \int\limits_0^a { x\left( { { a^2 } - 2ax + { x^2 } }\right)dx } } = \\ = { \frac { 1 } { 2 } \int\limits_0^a { \left( { { a^2 } x - 2a { x^2 } + { x^3 } }\right)dx } } = { \frac { 1 } { 2 } \left. { \left( { { a^2 } \cdot \frac { { { x^2 } } } { 2 } - 2a \cdot \frac { { { x^3 } } } { 3 } + \frac { { { x^4 } } } { 4 } }\right) }\right|_0^a } = { \frac { 1 } { 2 } \left( { \frac { { { a^2 } } } { 2 } - \frac { { 2 { a^4 } } } { 3 } + \frac { { { a^4 } } } { 4 } }\right) } = { \frac { { { a^4 } } } { { 24 } } . } $

Пример 6

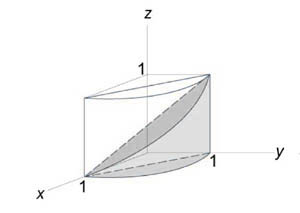
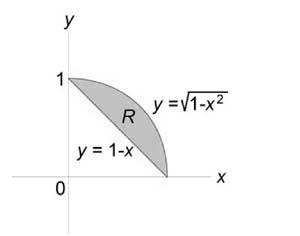
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( { x^2 } + { y^2 } = 1,) (z = 1 - x.)

Решение:

Как видно из рисунков, в области интегрирования (R) при (0 \le x \le 1) значения (y) изменяются от (1 - x) до (\sqrt { 1 - { x^2 } } .)

Сверху тело ограничено плоскостью (z = 1 - x.) Следовательно, объем данного тела равен $ { V = \iint\limits_R { \left( { 1 - x }\right)dxdy } } = { \int\limits_0^1 { \left[ { \int\limits_ { 1 - x } ^ { \sqrt { 1 - { x^2 } } } { \left( { 1 - x }\right)dy } }\right]dx } } = { \int\limits_0^1 { \left[ { \left( { 1 - x }\right)\left. y \right|_ { 1 - x } ^ { \sqrt { 1 - { x^2 } } } }\right]dx } } = { \int\limits_0^1 { \left( { 1 - x }\right)\left( { \sqrt { 1 - { x^2 } } - 1 + x }\right)dx } } = \\ = { \int\limits_0^1 { \left( { \sqrt { 1 - { x^2 } } - x\sqrt { 1 - { x^2 } } - 1 + 2x - { x^2 } }\right)dx } } = { \int\limits_0^1 { \sqrt { 1 - { x^2 } } dx } } - { \int\limits_0^1 { x\sqrt { 1 - { x^2 } } dx } } - { \int\limits_0^1 { \left( { 1 + 2x - { x^2 } }\right)dx } . } $

Вычислим полученные три интеграла отдельно. $ { I_1 } = \int\limits_0^1 { \sqrt { 1 - { x^2 } } dx } .$ Сделаем замену: (x = \sin t.) Тогда (dx = \cos tdt.) Видно, что (t = 0) при (x = 0) и (t = \large\frac { \pi } { 2 } \normalsize) при (x = 1.) Следовательно, $ { { I_1 } = \int\limits_0^1 { \sqrt { 1 - { x^2 } } dx } } = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sqrt { 1 - { { \sin } ^2 } t } \cos tdt } } = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { { { \cos } ^2 } tdt } } = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \frac { { 1 + \cos 2t } } { 2 } dt } } = { \frac { 1 } { 2 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \left( { 1 + \cos 2t }\right)dt } } = { \frac { 1 } { 2 } \left. { \left( { t + \frac { { \sin 2t } } { 2 } }\right) }\right|_0^ { \large\frac { \pi } { 2 } \normalsize } } = { \frac { 1 } { 2 } \left( { \frac { \pi } { 2 } + \frac { { \sin \pi } } { 2 } }\right) = \frac { \pi } { 4 } . } $ { Сравните с площадью сектора единичного круга в первом квадранте).

Вычислим второй интеграл ( { I_2 } = \int\limits_0^1 { x\sqrt { 1 - { x^2 } } dx } ,) используя замену переменной. Полагаем (1 - { x^2 } = w.) Тогда (-2xdx = dw) или (xdx = \large\frac { { - dw } } { 2 } \normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ { { I_2 } = \int\limits_0^1 { x\sqrt { 1 - { x^2 } } dx } } = { \int\limits_1^0 { \sqrt w \left( { - \frac { { dw } } { 2 } }\right) } } = { - \frac { 1 } { 2 } \int\limits_1^0 { \sqrt w dw } } = { \frac { 1 } { 2 } \int\limits_0^1 { \sqrt w dw } } = { \frac { 1 } { 2 } \int\limits_0^1 { { w^ { \large\frac { 1 } { 2 } \normalsize } } dw } } = { \frac { 1 } { 2 } \left. { \left( { \frac { { 2 { w^ { \large\frac { 3 } { 2 } \normalsize } } } } { 3 } }\right) }\right|_0^1 = \frac { 1 } { 3 } . } $ Наконец, вычислим третий интеграл. $\require { cancel } { { I_3 } = \int\limits_0^1 { \left( { 1 - 2x + { x^2 } }\right)dx } } = { \left. { \left( { x - { x^2 } + \frac { { { x^3 } } } { 3 } }\right) }\right|_0^1 } = { \cancel { 1 } - \cancel { 1 } + \frac { 1 } { 3 } = \frac { 1 } { 3 } . } $ Таким образом, объем тела равен $ { V = { I_1 } - { I_2 } - { I_3 } } = { \frac { \pi } { 4 } - \frac { 1 } { 3 } - \frac { 1 } { 3 } = \frac { \pi } { 4 } - \frac { 2 } { 3 } \approx 0,12. } $

Пример 7

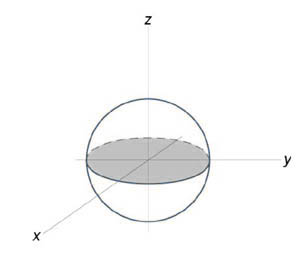
Вычислить объем единичного шара.

Решение:

Уравнение сферы радиусом (1) имеет вид ( { x^2 } + { y^2 } + { z^2 } = 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = \sqrt { 1 - \left( { { x^2 } + { y^2 } }\right) } .$ Преобразуя это уравнение в полярные координаты, получаем $z\left( { r,\theta }\right) = \sqrt { 1 - { r^2 } } .$ В полярных координатах область интегрирования (R) описывается множеством (R = \left[{ \left( { r,\theta }\right)|\;0 \le r \le 1,0 \le \theta \le 2\pi }\right].) Следовательно, объем верхнего полушара выражается формулой $ { { V_ { \large\frac { 1 } { 2 } \normalsize } } = \iint\limits_R { \sqrt { 1 - { r^2 } } rdrd\theta } } = { \int\limits_0^ { 2\pi } { d\theta } \int\limits_0^1 { \sqrt { 1 - { r^2 } } rdr } } = { 2\pi \int\limits_0^1 { \sqrt { 1 - { r^2 } } rdr } . } $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 - { r^2 } = t.) Тогда (-2rdr = dt) или (rdr = - \large\frac { { dt } } { 2 } \normalsize.) Уточним пределы интегрирования: (t = 1) при (r = 0) и, наоборот, (t = 0) при (r = 1.) Получаем $ { { V_ { \large\frac { 1 } { 2 } \normalsize } } = 2\pi \int\limits_0^1 { \sqrt { 1 - { r^2 } } rdr } } = { 2\pi \int\limits_1^0 { \sqrt t \left( { - \frac { { dt } } { 2 } }\right) } } = { - \pi \int\limits_1^0 { \sqrt t dt } } = { \pi \int\limits_0^1 { { t^ { \large\frac { 1 } { 2 } \normalsize } } dt } } = { \pi \left. { \left( { \frac { { { t^ { \large\frac { 3 } { 2 } \normalsize } } } } { { \frac { 3 } { 2 } } } }\right) }\right|_0^1 } = { \frac { { 2\pi } } { 3 } . } $ Таким образом, объем единичного шара равен $V = 2 { V_ { \large\frac { 1 } { 2 } \normalsize } } = \frac { { 4\pi } } { 3 } .$

Пример 8

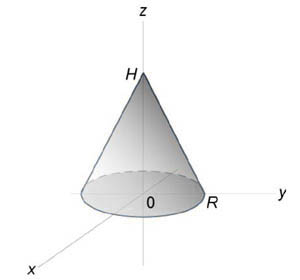
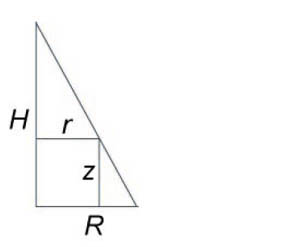
Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).

Решение:

Сначала получим уравнение поверхности конуса. Используя подобные треугольники, можно записать $ { \frac { r } { R } = \frac { { H - z } } { H } , } \;\; { \text { где } \;\;r = \sqrt { { x^2 } + { y^2 } } . } $ Следовательно, $ { H - z = \frac { { Hr } } { R } } \;\; { \text { или } \;\;z\left( { x,y }\right) } = { H - \frac { { Hr } } { R } } = { \frac { H } { R } \left( { R - r }\right) } = { \frac { H } { R } \left( { R - \sqrt { { x^2 } + { y^2 } } }\right). } $ Тогда объем конуса равен $ { V = \iint\limits_R { z\left( { x,y }\right)dxdy } } = { \iint\limits_R { \frac { H } { R } \left( { R - \sqrt { { x^2 } + { y^2 } } }\right)dxdy } } = { \frac { H } { R } \iint\limits_R { \left( { R - r }\right)rdrd\theta } } = { \frac { H } { R } \int\limits_0^ { 2\pi } { \left[ { \int\limits_0^R { \left( { R - r }\right)drd } }\right]d\theta } } = { \frac { H } { R } \int\limits_0^ { 2\pi } { d\theta } \int\limits_0^R { \left( { Rr - { r^2 } }\right)dr } } = { \frac { { 2\pi H } } { R } \int\limits_0^R { \left( { Rr - { r^2 } }\right)dr } } = \\ = { \frac { { 2\pi H } } { R } \left. { \left( { \frac { { R { r^2 } } } { 2 } - \frac { { { r^3 } } } { 3 } }\right) }\right|_ { r = 0 } ^R } = { \frac { { 2\pi H } } { R } \left( { \frac { { { R^3 } } } { 2 } - \frac { { { R^3 } } } { 3 } }\right) } = { \frac { { 2\pi H } } { R } \cdot \frac { { { R^3 } } } { 6 } = \frac { { \pi { R^2 } H } } { 3 } . } $