Свойства двойного интеграла

Постоянный множитель может быть вынесен за знак двойного интеграла

(\iint\limits_R { c\left( { x,y }\right)dA } = c\iint\limits_R { f\left( { x,y }\right)dA } ,) где (c) - константа;

Линейность

Если функции $\mathbf { \textit { f } } (\mathbf { \textit { x } } $, $\mathbf { \textit { y } } )$, $\mathbf { \textit { g } } (\mathbf { \textit { x } } $, $\mathbf { \textit { y } } )$ интегрируемы по области $\mathbf { \textit { D } } $, то их линейная комбинация $\alpha f(x,y)+\beta g(x,y)$ тоже интегрируема по области $\mathbf { \textit { D } } $, и $\iint\limits_D { \left[ { \alpha f(P)+\beta g(P) }\right]ds= } \alpha \iint\limits_D { f(P)ds } +\beta \iint\limits_D { g(P)ds } $.

Док-во:

Для интегральных сумм справедливо равенство

$$\sum\limits_ { i=1 } ^n { \left[ { \alpha f(P_i )+\beta g(P_i ) }\right]s(D_i ) } =\alpha \sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } +\beta \sum\limits_ { i=1 } ^n { g(P_i )s(D_i ) } $$

Переходя к пределу при $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n } diam(D_i )\to 0$ и пользуясь свойствами пределов, рассмотренными в разделе Арифметические действия с пределами { здесь должна быть ссылка, но пока ее нет } , получим требуемое равенство.

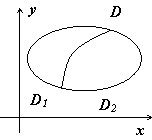
Аддитивность

Если область $\mathbf { \textit { D } } $ является объединением двух областей $\mathbf { \textit { D } } _ { 1 } $ и $\mathbf { \textit { D } } _ { 2 } $, не имеющих общих внутренних точек, то $\iint\limits_D { f(P)ds } =\iint\limits_ { D_1 } { f(P)ds } +\iint\limits_ { D_2 } { f(P)ds } $.

Док-во:

Пусть область $\mathbf { \textit { D } } _ { 1 } $ разбита на подобласти $\mathbf { \textit { D } } _ { 1,1 } $, $\mathbf { \textit { D } } _ { 1,2 } , { \ldots } , \mathbf { \textit { D } } _ { 1, n1 } $; область $\mathbf { \textit { D } } _ { 2 } $ разбита на подобласти $\mathbf { \textit { D } } _ { 2,1 } $, $\mathbf { \textit { D } } _ { 2,2 } , { \ldots } , \mathbf { \textit { D } } _ { 2, n2 } $. Тогда объединение этих разбиений даст разбиение области $\mathbf { \textit { D } } $: $D=\left( { \bigcup\limits_ { i_1 =1 } ^ { n_1 } { D_ { 1,i_1 } } }\right)\cup \left( { \bigcup\limits_ { i_2 =1 } ^ { n_2 } { D_ { 2,i_2 } } }\right)$ на $\mathbf { \textit { n } } _ { 1 } +\mathbf { \textit { n } } _ { 2 } $ подобластей. Интегральная сумма по области $\mathbf { \textit { D } } $ равна сумме сумм по областям $\mathbf { \textit { D } } _ { 1 } $ и $\mathbf { \textit { D } } _ { 2 } $: $\sum\limits_ { i=1 } ^ { n_1 +n_2 } { f(P_i )\cdot s(D_i ) } =\sum\limits_ { i_1 =1 } ^ { n_1 } { f(P_ { i_1 } )\cdot s(D_ { i_1 } ) } +\sum\limits_ { i_2 =1 } ^ { n_2 } { f(P_ { i_2 } )\cdot s(D_ { i_2 } ) } $. Как и в предыдущем случае, переходя к пределу при $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n;\;j=1,2 } diam(D_ { i_j } )\to 0$, получим требуемое равенство.

Интеграл от единичной функции по области

$\mathbf { \textit { D } } $ равен площади этой области: $\iint\limits_D { ds } =s(D)\textbf { . } $

Док-во:

Для любого разбиения $\sum\limits_ { i=1 } ^n { s(D_i ) } =s(D)$, т.е. не зависит ни от разбиения, ни от выбора точек $\mathbf { \textit { P } } _ { i } $. Предел постоянной равен этой постоянной, поэтому $\iint\limits_D { ds } =\mathop { \lim } \limits_ { d\to 0 } \sum\limits_ { i=1 } ^n { s(D_i ) } =s(D)$.

Интегрирование неравенств

Если в любой точке $P\in D$ выполняется неравенство $f(P)\leqslant g(P)$, и функции $\mathbf { \textit { f(P } } )$, $\mathbf { \textit { g } } (\mathbf { \textit { P } } )$ интегрируемы по области $\mathbf { \textit { D } } $, то $\iint\limits_D { f(P)ds } \leqslant \iint\limits_D { g(P)ds } $.

Док-во:

В любой точке $P_i \in D$ выполняется неравенство $f(P)\leqslant g(P)$, поэтому $\sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } \leqslant \sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } $. По теореме о переходе к пределу в неравенствах отсюда следует требуемое утверждение.

Теоремы об оценке интеграла

Если функция $\mathbf { \textit { f(P } } )$ интегрируема по области $\mathbf { \textit { D } } $ и для $\forall P\in D$ выполняется $m\leqslant f(P)\leqslant M$, то $m\cdot s(D)\leqslant \iint\limits_D { f(P)ds } \leqslant M\cdot s(D)$.

Док-во:

$m\leqslant f(P)\leqslant M \quad \mathop \Rightarrow \limits^ { ссылки-еще-нет } \quad \sum\limits_ { i=1 } ^n { m\cdot s(D_i ) } \leqslant \sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } \leqslant \sum\limits_ { i=1 } ^n { M\cdot s(D_i ) } \mathop \Rightarrow \limits^ { ссылки-еще-нет } \\ \quad \mathop \Rightarrow \limits^ { ссылки-еще-нет } m\sum\limits_ { i=1 } ^n { s(D_i ) } \leqslant \sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } \leqslant M\sum\limits_ { i=1 } ^n { s(D_i ) } \mathop \Rightarrow \limits^ { ссылки-еще-нет } m\cdot s(D)\leqslant \iint\limits_D { f(P)ds } \leqslant M\cdot s(D)$

Цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств.

Если функция $\mathbf { \textit { f(P } } )$ интегрируема по области $\mathbf { \textit { D } } $, то $\left| { \iint\limits_D { f(P)ds } }\right|\leqslant \iint\limits_D { \vert f(P)\vert ds } $.

Док-во:

Эти неравенства непосредственно следуют из того, что $-\vert f(P)\vert \leqslant f(P)\leqslant \vert f(P)\vert $ и свойства Интегрирование неравенств

Теорема о среднем

Если функция $\mathbf { \textit { f(P } } )$ непрерывна на области $\mathbf { \textit { D } } $, то существует точка $P_0 \in D$, такая что $\iint\limits_D { f(P)ds } =f(P_0 )\cdot s(D)$.

Док-во:

Непрерывная на ограниченной замкнутой области $\mathbf { \textit { D } } $ функция $\mathbf { \textit { f(P } } )$ принимает в некоторых точках этой области своё минимальное $\mathbf { \textit { m } } $ и максимальное $\mathbf { \textit { M } } $ значения. Так как $m\leqslant f(P)\leqslant M$, то $m\cdot s(D)\leqslant \iint\limits_D { f(P)ds } \leqslant M\cdot s(D)$, или $m\leqslant \frac { 1 } { s(D) } \iint\limits_D { f(P)ds } \leqslant M$. Непрерывная функция принимает, кроме того, любое значение, заключённое между $\mathbf { \textit { m } } $ и $\mathbf { \textit { M } } $, в частности, значение

$\frac { 1 } { s(D) } \iint\limits_D { f(P)ds } \leqslant M$. Следовательно, $\exists P_0 \in D\vert \;f(P_0 )=\frac { 1 } { s(D) } \iint\limits_D { f(P)ds } $, откуда и следует доказываемое утверждение.