Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Смысл этих задач - научиться быстро определять параметры $a,\;b,\;\varphi _1 (x),\;\varphi _2 (x),\;c,\;d,\;\psi _1 (y),\;\psi _2 (y)$ { в декартовых координатах } и $\varphi _0 ,\;\varphi _2 ,\;r_1 (\varphi ),\;r_2 (\varphi )$ { в полярных координатах } , необходимые для перехода от двойного интеграла к повторному.

Примеры:

Пример 1

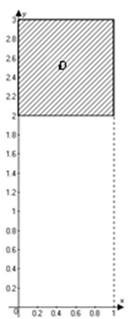
Пусть область $D=\left[{ x\leqslant 0,\;y\leqslant 0,\;x^2+y^2\leqslant 4 }\right]\cup \left[{ x\geqslant 0,\;x^2+y^2\leqslant -2y }\right]$. Представить двойной интеграл по области $\mathbf { \textit { D } } $ в виде повторных. Перейти к полярным координатам. 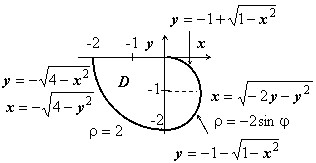Решение:

Область изображена на рисунке. Для левой части $D-2\leqslant x\leqslant 0;\quad -\sqrt { 4-x^2 } \leqslant y\leqslant 0$; для правой - $0\leqslant x\leqslant 1,\;-1-\sqrt { 1-x^2 } \leqslant y\leqslant -1+\sqrt { 1-x^2 } $ уравнение правой полуокружности после выделения полных квадратов принимает вид $x^2+(y+1)^2=1$, поэтому

$$ I=\iint\limits_D { f(x,y)dxdy } =\int\limits_ { -2 } ^0 { dx\int\limits_ { -\sqrt { 4-x^2 } } ^0 { f(x,y)dy } } +\int\limits_0^1 { dx\int\limits_ { -1-\sqrt { 1-x^2 } } ^ { -1+\sqrt { 1-x^2 } } { f(x,y)dy } } . $$

$\mathbf { \textit { D } } $ можно также oписать неравенствами $-2\leqslant y\leqslant 0,\;-\sqrt { 4-y^2 } \leqslant x\leqslant \sqrt { -2y-y^2 } $, поэтому $I=\iint\limits_D { f(x,y)dxdy } =\int\limits_ { -2 } ^0 { dy\int\limits_ { -\sqrt { 4-y^2 } } ^ { \sqrt { -2y-y^2 } } { f(x,y)dx } } $. В полярных координатах уравнение левой четверти окружности имеет вид $r=2$ для $\pi \leqslant \varphi \leqslant 3\pi /2$ { можно взять и отрезок $-\pi \leqslant \varphi \leqslant -\pi /2$ } , правой полуокружности $r=-2\sin \varphi $ для $3\pi /2\leqslant \varphi \leqslant 2\pi $ { можно взять и отрезок $-\pi /2\leqslant \varphi \leqslant 0$ } , поэтому $I=\iint\limits_D { f(x,y)dxdy } =\iint\limits_ { D_ { r,\varphi } } { f(r\cos \varphi ,r\sin \varphi )rdrd\varphi } =\int\limits_\pi ^ { 3\pi /2 } { d\varphi \int\limits_0^2 { f(r\cos \varphi ,r\sin \varphi )rdr } } + \\ + \int\limits_ { 3\pi /2 } ^ { 2\pi } { d\varphi \int\limits_0^ { -2\sin \varphi } { f(r\cos \varphi ,r\sin \varphi )rdr } } $

Пример 2

Изменить порядок интегрирования, перейти к полярным координатам. 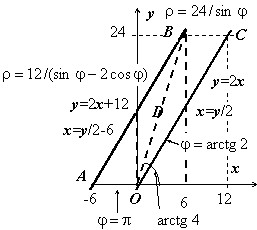$I=\int\limits_ { -6 } ^0 { dx\int\limits_0^ { 2x+12 } { f(x,y)dy } } +\int\limits_0^6 { dx\int\limits_ { 2x } ^ { 2x+12 } { f(x,y)dy } } +\int\limits_6^ { 12 } { dx\int\limits_ { 2x } ^ { 24 } { f(x,y)dy } } $

Решение:

Область $\mathbf { \textit { D } } $ - объединение трёх подобластей: $D=\left[{ -6\leqslant x\leqslant 0,\;0\leqslant y\leqslant 2x+12 }\right]\cup \left[{ 0\leqslant x\leqslant 6,\;2x\leqslant y\leqslant 2x+12 }\right]\cup\left[{ 6\leqslant x\leqslant 12,\;2x\leqslant y\leqslant 24 }\right]\cup $

На рисунке изображена область и приведены уравнения прямых и обратных функций для линий, ограничивающих её. $\mathbf { \textit { D } } $ можно представить в виде $D=\left[{ 0\leqslant y\leqslant 24,\;y/2-6\leqslant x\leqslant y/2 }\right]$, поэтому $I=\int\limits_0^ { 24 } { dy\int\limits_ { y/2-6 } ^ { y/2 } { f(x,y)dx } } $. В полярных координатах $\mathbf { \textit { D } } $ представляется как объединение двух треугольников $\mathbf { \textit { OCB } } $и $\mathbf { \textit { OBA } } $. Уравнение прямой $\mathbf { \textit { ОС } } $: $\varphi =arctg2$ { можно получить и формально, перейдя к полярным координатам в её уравнении: $y=2x\Rightarrow \quad r\sin \varphi =2r\cos \varphi \Rightarrow tg\varphi =2$ } , прямой $\mathbf { \textit { ОВ } } $: $\varphi =arctg4$, прямой $\mathbf { \textit { СВ } } $: $y=24\Rightarrow r\sin \varphi =24\Rightarrow \quad r=24/\sin \varphi $, прямой $\mathbf { \textit { ОА } } $: $\varphi =\pi $, прямой $\mathbf { \textit { АВ } } $: $y=2x+12\Rightarrow r\sin \varphi =2r\cos \varphi +12\Rightarrow \quad r=\frac { 12 } { \sin \varphi -2\cos \varphi } $.

В результате $I=\iint\limits_D { f(x,y)dxdy } =\iint\limits_ { D_ { r,\varphi } } { f(r\cos \varphi ,r\sin \varphi )rdrd\varphi } =\\ \quad =\int\limits_ { arctg2 } ^ { arctg4 } { d\varphi \int\limits_0^ { 24/\sin \varphi } { f(r\cos \varphi ,r\sin \varphi )rdr } } +\int\limits_ { arctg4 } ^\pi { d\varphi \int\limits_0^ { 12/(\sin \varphi -2\cos \varphi ) } { f(r\cos \varphi ,r\sin \varphi )rdr } } $.

Пример 3

Вычислить двойной интеграл $\iint\limits_ { D } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dxdy } $, где область $D$ – квадрат со сторонами $x=0$, $x=1$, $y=2$, $y=3$. В повторном интеграле внутренний интеграл вначале вычислить по переменной $y$, а внешний – по $x$. Вычислить этот же интеграл, изменив порядок интегрирования.

Решение:

Вначале изобразим область интегрирования. Запишем заданный двойной интеграл через повторные: $\iint\limits_ { D } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dxdy } =\int\limits_ { 0 } ^ { 1 } { dx } \int\limits_ { 2 } ^ { 3 } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dy } $.

Внутреннее { первое } интегрирование будем выполнять по переменной $y$ { при этом считаем, что $x$ – константа } , а внешнее { второе } – по переменной $x$:

$$\iint\limits_ { D } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dxdy } =\int\limits_ { 0 } ^ { 1 } { dx } \int\limits_ { 2 } ^ { 3 } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dy } =$$

$$=\int\limits_ { 0 } ^ { 1 } { dx } \left[ 6x\int\limits_ { 2 } ^ { 3 } { { { y } ^ { 2 } } dy } -12 { { x } ^ { 2 } } \int\limits_ { 2 } ^ { 3 } { ydy }\right]=\int\limits_ { 0 } ^ { 1 } { \left( 6x\cdot \left. \frac { { { y } ^ { 3 } } } { 3 }\right|_ { 2 } ^ { 3 } -12 { { x } ^ { 2 } } \cdot \left. \frac { { { y } ^ { 2 } } } { 2 }\right|_ { 2 } ^ { 3 }\right)dx } =$$

$$=\int\limits_ { 0 } ^ { 1 } { \left[ 2x\left( { { 3 } ^ { 3 } } - { { 2 } ^ { 3 } }\right)-6 { { x } ^ { 2 } } \left( { { 3 } ^ { 2 } } - { { 2 } ^ { 2 } }\right) \right]dx } =\int\limits_ { 0 } ^ { 1 } { \left( 38x-30 { { x } ^ { 2 } }\right)dx } =$$

$$=\int\limits_ { 0 } ^ { 1 } { 38xdx } -\int\limits_ { 0 } ^ { 1 } { 30 { { x } ^ { 2 } } dx } =38\int\limits_ { 0 } ^ { 1 } { xdx } -30\int\limits_ { 0 } ^ { 1 } { { { x } ^ { 2 } } dx } =38\cdot \left. \frac { { { x } ^ { 2 } } } { 2 }\right|_ { 0 } ^ { 1 } -30\cdot \left. \frac { { { x } ^ { 3 } } } { 3 }\right|_ { 0 } ^ { 1 } =$$

$$=19\left( { { 1 } ^ { 2 } } - { { 0 } ^ { 2 } }\right)-10\left( { { 1 } ^ { 3 } } - { { 0 } ^ { 3 } }\right)=19-10=9$$

Вычислим теперь заданный по условию двойной интеграл, сменив порядок интегрирования: внутреннее интегрирование будем проводить по переменной $x$ { считая, что $y$ есть постоянной } , а внешнее – по переменной $y$:

$$\iint\limits_ { D } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dxdy } =\int\limits_ { 2 } ^ { 3 } { dy } \int\limits_ { 0 } ^ { 1 } { \left( 6x { { y } ^ { 2 } } -12 { { x } ^ { 2 } } y \right)dx } =$$

$$=\int\limits_ { 2 } ^ { 3 } { \left[ 6 { { y } ^ { 2 } } \int\limits_ { 0 } ^ { 1 } { xdx } -12y\int\limits_ { 0 } ^ { 1 } { { { x } ^ { 2 } } dx }\right]dy } =\int\limits_ { 2 } ^ { 3 } { \left[ 6 { { y } ^ { 2 } } \cdot \left. \frac { { { x } ^ { 2 } } } { 2 }\right|_ { 0 } ^ { 1 } -12y\cdot \left. \frac { { { x } ^ { 3 } } } { 3 }\right|_ { 0 } ^ { 1 }\right]dy } =$$

$$=\int\limits_ { 2 } ^ { 3 } { \left( 3 { { y } ^ { 2 } } -4y \right)dy } =\left. \left( 3\cdot \frac { { { y } ^ { 3 } } } { 3 } -4\cdot \frac { { { y } ^ { 2 } } } { 2 }\right) \right|_ { 2 } ^ { 3 } =27-8-2\left( 9-4 \right)=19-10=9$$

Пример 4

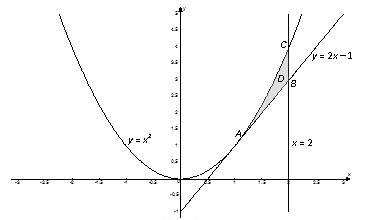
Вычислить двойной интеграл $\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } $, если область $D$ ограничена линиями $y= { { x } ^ { 2 } } $, $x=2$, $y=2x-1$. Вычислить этот же интеграл, изменив порядок интегрирования.

Решение:

Строим заданную область $D$. Вначале внутреннее интегрирование будем проводить по переменной $y$, а внешнее – по $x$: $$\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } =\int\limits_ { a } ^ { b } { dx } \int\limits_ { { { \phi } _ { 1 } } \left( x \right) } ^ { { { \phi } _ { 2 } } \left( x \right) } { \left( { { x } ^ { 2 } } +2y \right)dy } $$

Контур области $D$ пересекается любой прямой, параллельной оси ординат, в двух точках.

Найдем пределы интегрирования. Переменная $x$ изменяется от абсциссы точки $A$ к абсциссе точек $B$ и $C$. Координаты точки $A$ найдем как координаты точки пересечения графиков функций $y= { { x } ^ { 2 } } $ и $y=2x-1$:

$$\left[ \begin { matrix } y= { { x } ^ { 2 } } , \\ y=2x-1 \\ \end { matrix }\right.\Rightarrow { { x } ^ { 2 } } =2x-1\Rightarrow { { x } ^ { 2 } } -2x+1=0\Rightarrow { { \left( x-1 \right) } ^ { 2 } } =0\Rightarrow { { x } _ { A } } =1$$

Так как точки $B$ и $C$ лежать на прямой $x=2$, то $ { { x } _ { B } } = { { x } _ { C } } =2$. Итак, $1\le x\le 2$. Далее на отрезке $\left[ 1;\ 2 \right]$ выбираем произвольную точку $x$, через нее проводим прямую, параллельную оси $Oy$, и на этой прямой рассмотрим отрезок $KL$, принадлежащий области $D$.

Область $D$ ограничена снизу прямой $y=2x-1$, а сверху – веткой параболы $y= { { x } ^ { 2 } } $. Переменная $y$ изменяется в заданной области $D$ от ее значения $2x-1$ на нижней части контура $ABC$ до ее значения $ { { x } ^ { 2 } } $ на верхней части этого контура.

Замечание. Уравнения линий, ограничивающих контур, должны быть разрешены относительно той переменной, относительно которой находится внутренний интеграл.

Таким образом, $2x-1\le y\le { { x } ^ { 2 } } $, а тогда область $D$ задается следующими неравенствами:

$$D:\left[ \begin { matrix } 1\le x\le 2, \\ 2x-1\le y\le { { x } ^ { 2 } } . \\ \end { matrix }\right.$$

Итак,

$$\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } =\int\limits_ { 1 } ^ { 2 } { dx } \int\limits_ { 2x-1 } ^ { { { x } ^ { 2 } } } { \left( { { x } ^ { 2 } } +2y \right)dy } =\int\limits_ { 1 } ^ { 2 } { dx } \left. \left( { { x } ^ { 2 } } y+ { { y } ^ { 2 } }\right) \right|_ { 2x-1 } ^ { { { x } ^ { 2 } } } =$$

$$=\int\limits_ { 1 } ^ { 2 } { \left[ { { x } ^ { 2 } } \cdot { { x } ^ { 2 } } + { { \left( { { x } ^ { 2 } }\right) } ^ { 2 } } -\left( { { x } ^ { 2 } } \cdot \left( 2x-1 \right)+ { { \left( 2x-1 \right) } ^ { 2 } }\right) \right]dx } =$$

$$=\int\limits_ { 1 } ^ { 2 } { \left( 2 { { x } ^ { 4 } } -2 { { x } ^ { 3 } } -3 { { x } ^ { 2 } } +4x-1 \right)dx } =\left. \left( \frac { 2 { { x } ^ { 5 } } } { 5 } -\frac { { { x } ^ { 4 } } } { 2 } - { { x } ^ { 3 } } +2 { { x } ^ { 2 } } -x \right) \right|_ { 1 } ^ { 2 } =$$

$$=\frac { 64 } { 5 } -8-8+8-2-\left( \frac { 2 } { 5 } -\frac { 1 } { 2 } -1+2-1 \right)=\frac { 29 } { 10 } $$

Вычислим теперь рассматриваемый двойной интеграл, изменив порядок интегрирования: внутреннее интегрирование будем проводить по переменной $x$, а внешнее – по $y$. То есть, перейдя к повторным интегралам, получим:

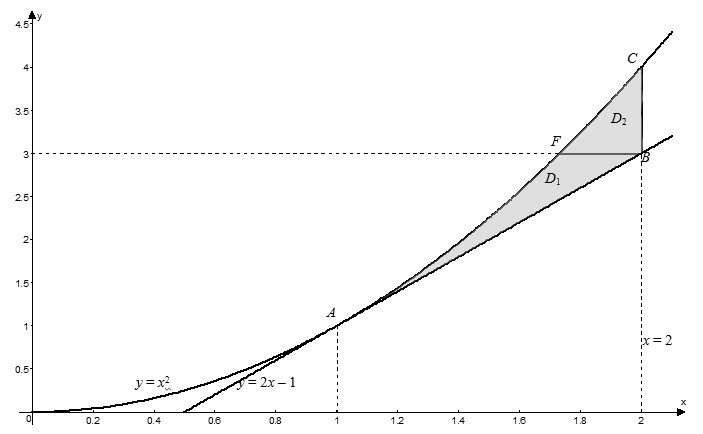
$$\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } =\int\limits_ { c } ^ { d } { dy } \int\limits_ { { { \psi } _ { 1 } } \left( y \right) } ^ { { { \psi } _ { 2 } } \left( y \right) } { \left( { { x } ^ { 2 } } +2y \right)dx } $$ 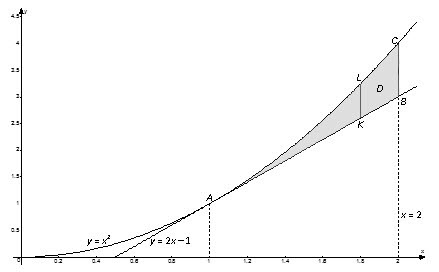Из рисунка в области $D$ видно, что левая граница контура области – одна линия { положительная ветка параболы $y= { { x } ^ { 2 } } $), а его правая часть состоит из двух линий $AB$ { отрезок прямой $y=2x-1$) и $BC$ { отрезок прямой $x=2$), то есть задается разными уравнениями. В этом случае область $D$ нужно разбить на части так, чтобы каждая из них справа была ограничена только одной линией. В данном случае такими частями будут $ { { D } _ { 1 } } -ABF$ и $ { { D } _ { 2 } } -BCF$. Заданная область $D$ будет суммой областей $ { { D } _ { 1 } } $ и $ { { D } _ { 2 } } $. Тогда искомый интеграл будет равен сумме интегралов по каждой из областей:

$$\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } =\iint\limits_ { { { D } _ { 1 } } } { \left( { { x } ^ { 2 } } +2y \right)dxdy } +\iint\limits_ { { { D } _ { 2 } } } { \left( { { x } ^ { 2 } } +2y \right)dxdy } $$

Поскольку в данном случае внутреннее интегрирование проводится по переменной $x$, то уравнения ограничивающих линий нужно разрешить относительно этой переменной:

$$AB:y=2x-1\Rightarrow x=\frac { y+1 } { 2 } ; \qquad AC:y= { { x } ^ { 2 } } \Rightarrow x=\sqrt { y } $$

Найдем пределы интегрирования для каждой из областей. В области $ { { D } _ { 1 } } $ переменная $y$ изменяется от ординаты точки $A$ до ординат точек $B$ и $F$. Точка $A$ принадлежит параболе $y= { { x } ^ { 2 } } $ и выше было найдено, что абсцисса этой точки $ { { x } _ { A } } =1$, тогда $ { { y } _ { A } } = { { 1 } ^ { 2 } } =1$. Точка $B$ – точка пересечения двух прямых $x=2$ и $y=2x-1$, а тогда $ { { y } _ { B } } =2\cdot 2-1=3$. Итак имеем, что $1\le y\le 3$. Переменная $x$ в области $ { { D } _ { 1 } } $ изменяется от ветки параболы $x=\sqrt { y } $ до прямой $x=\frac { y+1 } { 2 } $, то есть $ { { D } _ { 1 } } :\left[ \begin { matrix } 1\le y\le 3, \\ \sqrt { y } \le x\le \frac { y+1 } { 2 } . \\ \end { matrix }\right.$ Аналогично для области $ { { D } _ { 2 } } $ находим, что $ { { D } _ { 2 } } :\left[ \begin { matrix } 3\le y\le 4, \\ \sqrt { y } \le x\le 2. \\ \end { matrix }\right.$

Таким образом,

$$\iint\limits_ { D } { \left( { { x } ^ { 2 } } +2y \right)dxdy } =\int\limits_ { 1 } ^ { 3 } { dy } \int\limits_ { \sqrt { y } } ^ { \frac { y+1 } { 2 } } { \left( { { x } ^ { 2 } } +2y \right)dx } +\int\limits_ { 3 } ^ { 4 } { dy } \int\limits_ { \sqrt { y } } ^ { 2 } { \left( { { x } ^ { 2 } } +2y \right)dx } =$$

$$=\int\limits_ { 1 } ^ { 3 } { \left. \left( \frac { { { x } ^ { 3 } } } { 3 } +2xy \right) \right|_ { \sqrt { y } } ^ { \frac { y+1 } { 2 } } dy } +\int\limits_ { 3 } ^ { 4 } { \left. \left( \frac { { { x } ^ { 3 } } } { 3 } +2xy \right) \right|_ { \sqrt { y } } ^ { 2 } dy } =$$

$$=\int\limits_ { 1 } ^ { 3 } { \left( \frac { { { \left( y+1 \right) } ^ { 3 } } } { 24 } + { { y } ^ { 2 } } +y-\frac { 7 } { 3 } { { y } ^ { \frac { 3 } { 2 } } }\right)dy } +\int\limits_ { 3 } ^ { 4 } { \left( \frac { 8 } { 3 } +4y-\frac { 7 } { 3 } { { y } ^ { \frac { 3 } { 2 } } }\right)dy } =$$

$$=\left. \left[ \frac { { { \left( y+1 \right) } ^ { 4 } } } { 96 } +\frac { { { y } ^ { 3 } } } { 3 } +\frac { { { y } ^ { 2 } } } { 2 } -\frac { 14 } { 15 } \sqrt { { { y } ^ { 5 } } }\right] \right|_ { 1 } ^ { 3 } +\left. \left[ \frac { 8y } { 3 } +2 { { y } ^ { 2 } } -\frac { 14 } { 15 } \sqrt { { { y } ^ { 5 } } }\right] \right|_ { 3 } ^ { 4 } =$$

$$=\left[ \frac { 8 } { 3 } +9+\frac { 9 } { 2 } -\frac { 42\sqrt { 3 } } { 5 } -\left( \frac { 1 } { 6 } +\frac { 1 } { 3 } +\frac { 1 } { 2 } -\frac { 14 } { 15 }\right) \right]+$$

$$+\left[ \frac { 32 } { 3 } +32-\frac { 448 } { 15 } -\left( 8+18-\frac { 42\sqrt { 3 } } { 5 }\right) \right]=\frac { 29 } { 10 } $$

Пример 5

Вычислить двойной интеграл (\iint\limits_R { \left( { { x^2 } + { y^2 } }\right)dydx } ,) преобразовав его в полярные координаты. Область интегрирования (R) представляет собой сектор (0 \le \theta \le \large\frac { \pi } { 2 } \normalsize) круга радиусом (r = \sqrt 3.)

Решение: Область (R) в полярных координатах описывается множеством (R = \left[{ \left( { r,\theta }\right)|\;0 \le r \le \sqrt 3 ,0 \le \theta \le \large\frac { \pi } { 2 } \normalsize }\right]) (рисунок (4)). Применяя формулу $ { \iint\limits_R { f\left( { x,y }\right)dxdy } } = { \int\limits_\alpha ^\beta { \int\limits_ { a } ^ { b } { f\left( { r\cos \theta ,r\sin \theta }\right)rdrd\theta } } , } $ получаем $ { \iint\limits_R { \left( { { x^2 } + { y^2 } }\right)dydx } } = { \int\limits_0^ { \frac { \pi } { 2 } } { \int\limits_0^ { \sqrt 3 } { { r^2 } \left( { { { \cos } ^2 } \theta + { { \sin } ^2 } \theta }\right)rdrd\theta } } } = { \int\limits_0^ { \frac { \pi } { 2 } } { d\theta } \int\limits_0^ { \sqrt 3 } { { r^3 } dr } } = { \left. \theta \right|_0^ { \frac { \pi } { 2 } } \cdot \left. { \left( { \frac { { { r^4 } } } { 4 } }\right) }\right|_0^ { \sqrt 3 } } = { \frac { \pi } { 2 } \cdot \frac { 9 } { 4 } = \frac { { 9\pi } } { 8 } . } $

Пример 6

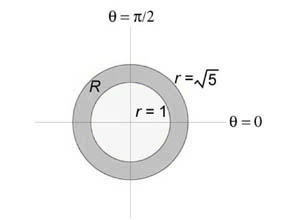
Вычислить интеграл (\iint\limits_R { xydydx } ,) в котором область интегрирования (R) представляет собой кольцо, ограниченное окружностями ( { x^2 } + { y^2 } = 1) и ( { x^2 } + { y^2 } = 5.)

Решение:

В полярных координатах область интегрирования (R) является полярным прямоугольником: $R = \left( { \left( { r,\theta }\right)|\;1 \le r \le \sqrt 5 ,0 \le \theta \le 2\pi }\right).$

Тогда, используя формулу $ { \iint\limits_R { f\left( { x,y }\right)dxdy } } = { \int\limits_\alpha ^\beta { \int\limits_ { a } ^ { b } { f\left( { r\cos \theta ,r\sin \theta }\right)rdrd\theta } } , } $ находим значение интеграла $ { \iint\limits_R { xydydx } } = { \int\limits_0^ { 2\pi } { \int\limits_1^ { \sqrt 5 } { r\cos \theta r\sin \theta rdrd\theta } } } = { \int\limits_0^ { 2\pi } { \sin \theta \cos \theta d\theta } \int\limits_1^ { \sqrt 5 } { { r^3 } dr } } = { \frac { 1 } { 2 } \int\limits_0^ { 2\pi } { \sin 2\theta d\theta } \int\limits_1^ { \sqrt 5 } { { r^3 } dr } } = { \frac { 1 } { 2 } \left. { \left( { - \frac { { \cos 2\theta } } { 2 } }\right) }\right|_0^ { 2\pi } \cdot \left. { \left( { \frac { { { r^4 } } } { 4 } }\right) }\right|_1^ { \sqrt 5 } } = \\ = { \frac { 1 } { 4 } \left( { - \cos 4\pi + \cos 0 }\right) \cdot \frac { 1 } { 4 } \left( { 25 - 1 }\right) } = { \frac { 1 } { 4 } \left( { - 1 + 1 }\right) \cdot 6 = 0. } $

Пример 7

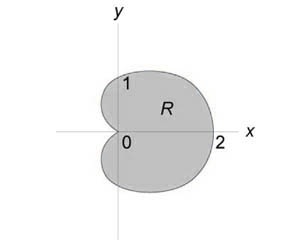
Найти интеграл (\iint\limits_R { \sin \theta drd\theta } ,) где область интегрирования (R) ограничена кардиоидой (r = 1 + \cos \theta ).

Решение:

Данный интеграл уже записан в полярных координатах. Выражая его через повторный интеграл, получаем: $\require { cancel } { \iint\limits_R { \sin \theta drd\theta } } = { \int\limits_0^ { 2\pi } { \int\limits_0^ { 1 + \cos \theta } { \sin \theta drd\theta } } } = { \int\limits_0^ { 2\pi } { \left[ { \int\limits_0^ { 1 + \cos \theta } { dr } }\right]\sin \theta d\theta } } = { \int\limits_0^ { 2\pi } { \left[ { \left. r \right|_0^ { 1 + \cos \theta } }\right]\sin \theta d\theta } } = { \int\limits_0^ { 2\pi } { \left( { 1 + \cos\theta }\right)\sin \theta d\theta } } = \\ = { \int\limits_0^ { 2\pi } { \left( { \sin \theta + \cos\theta \sin \theta }\right)d\theta } } = { \int\limits_0^ { 2\pi } { \sin \theta d\theta } + \int\limits_0^ { 2\pi } { \frac { { \sin 2\theta } } { 2 } d\theta } } = { \left. { \left( { - \cos \theta }\right) }\right|_0^ { 2\pi } + \frac { 1 } { 2 } \left. { \left( { - \frac { { \cos 2\theta } } { 2 } }\right) }\right|_0^ { 2\pi } } = { - \cos 2\pi + \cos 0 - \frac { 1 } { 4 } \cos 4\pi + \frac { 1 } { 4 } \cos 0 } = \\ = { -\cancel { 1 } + \cancel { 1 } - \cancel { \frac { 1 } { 4 } } + \cancel { \frac { 1 } { 4 } } = 0. } $

Пример 8

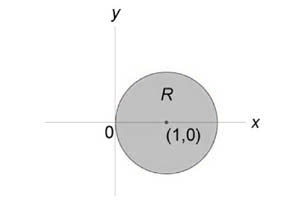
Вычислить интеграл (\iint\limits_R { \left( { { x^2 } + { y^2 } }\right)dxdy } ) в круге ( { x^2 } + { y^2 } = 2x.)

Решение: Область интегрирования (R) показана на рисунке:

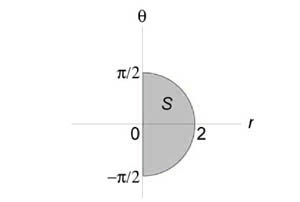
Преобразуем уравнение окружности следующим образом: $ { { x^2 } + { y^2 } = 2x, } \;\; { \Rightarrow { x^2 } - 2x + 1 + { y^2 } = 1, } \;\; { \Rightarrow { \left( { x - 1 }\right)^2 } + { y^2 } = 1. } $ Подставляя (x = r\cos \theta ,) (y = r\sin \theta ,) найдем уравнение окружности в полярных координатах. $ { { x^2 } + { y^2 } = 2x, } \;\; { \Rightarrow { r^2 } { \cos ^2 } \theta + { r^2 } { \sin^2 } \theta = 2r\cos \theta , } \;\; { \Rightarrow { r^2 } \left( { { { \cos } ^2 } \theta + { \sin^2 } \theta }\right) = 2r\cos \theta , } \;\; { \Rightarrow r = 2\cos \theta . } $ Образ (S) области интегрирования (R) показан на рисунке:

После перехода к полярным координатам вычисляем двойной интеграл. $ { \iint\limits_R { \left( { { x^2 } + { y^2 } }\right)dxdy } } = { \iint\limits_S { \left( { { r^2 } { { \cos } ^2 } \theta + { r^2 } { \sin^2 } \theta }\right)rdrd\theta } } = { \iint\limits_S { { r^3 } drd\theta } } = { \int\limits_ { - \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { \left[ { \int\limits_0^ { 2\cos \theta } { { r^3 } dr } }\right]d\theta } } = { 4\int\limits_ { - \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { \left[ { \left. { \left( { \frac { { { r^4 } } } { 4 } }\right) }\right|_0^ { 2\cos \theta } }\right]d\theta } } = { 4\int\limits_ { - \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { { { \cos } ^4 } \theta d\theta } } = \\ = { 4\int\limits_ { - \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { { { \left( { \frac { { 1 + \cos 2\theta } } { 2 } }\right) } ^2 } d\theta } } = { \int\limits_ { - \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { \left( { 1 + 2\cos 2\theta + { { \cos } ^2 } 2\theta }\right)d\theta } } = { \int\limits_ { - \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { \left( { 1 + 2\cos 2\theta + \frac { { 1 + \cos 4\theta } } { 2 } }\right)d\theta } } = { \int\limits_ { - \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } { \left( { \frac { 3 } { 2 } + 2\cos 2\theta + \frac { 1 } { 2 } \cos 4\theta }\right)d\theta } } = \\ = { \left. { \left( { \frac { 3 } { 2 } \theta + \sin 2\theta + \frac { 1 } { 8 } \sin 4\theta }\right) }\right|_ { - \large\frac { \pi } { 2 } \normalsize } ^ { \large\frac { \pi } { 2 } \normalsize } } = { \left( { \frac { 3 } { 2 } \cdot \frac { \pi } { 2 } + \sin \pi + \frac { 1 } { 8 } \sin 2\pi }\right) - \left( { - \frac { 3 } { 2 } \cdot \frac { \pi } { 2 } - \sin \pi - \frac { 1 } { 8 } \sin 2\pi }\right) } = { \frac { { 3\pi } } { 2 } . } $

Пример 9

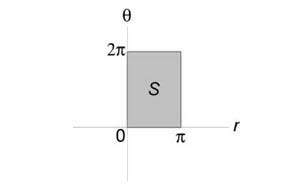
Вычислить двойной интеграл (\iint\limits_R { \sin \sqrt { { x^2 } + { y^2 } } dxdy } ) посредством преобразования в полярные координаты. Область интегрирования (R) представляет собой круг ( { x^2 } + { y^2 } \le { \pi ^2 } .)

Решение:

Область интегрирования (R) представлена на рисунке: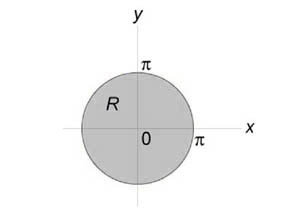

Образ (S) данной области описывается множеством (\left[{ S = \left( { r,\theta }\right)|\;0 \le r \le \pi ,0 \le \theta \le 2\pi }\right]) и показан на рисунке:

Запишем исходный двойной интеграл в полярных координатах. $ { I = \iint\limits_R { \sin \sqrt { { x^2 } + { y^2 } } dxdy } } = { \iint\limits_S { \sin \sqrt { { r^2 } { { \cos } ^2 } \theta + { r^2 } { \sin^2 } \theta } rdrd\theta } } = { \iint\limits_S { r\sin rdrd\theta } } = { \int\limits_0^ { 2\pi } { d\theta } \int\limits_0^\pi { r\sin rdr } } = { 2\pi \int\limits_0^\pi { r\sin rdr } . } $ Вычислим последний интеграл с помощью интегрирования по частям: $ { \int\limits_a^b { udv } } = { \left. { \left( { uv }\right) }\right|_a^b - \int\limits_a^b { vdu } . } $ Пусть (u = r,) (dv = \sin rdr.) Тогда (du = dr,\;\;v = \int { \sin rdr } = - \cos r). Следовательно, $ { I = 2\pi \int\limits_0^\pi { r\sin rdr } } = { 2\pi \left[ { \left. { \left( { - r\cos r }\right) }\right|_0^\pi - \int\limits_0^\pi { \left( { - \cos r }\right)dr } }\right] } = { 2\pi \left[ { \left. { \left( { - r\cos r }\right) }\right|_0^\pi + \int\limits_0^\pi { \cos rdr } }\right] } = \\ = { 2\pi \left[ { \left. { \left( { - r\cos r }\right) }\right|_0^\pi + \left. { \left( { \sin r }\right) }\right|_0^\pi }\right] } = { 2\pi \left. { \left( { \sin r - r\cos r }\right) }\right|_0^\pi } = { 2\pi \left[ { \left( { \sin \pi - \pi \cos \pi }\right) - \left( { \sin 0 - 0 \cdot \cos 0 }\right) }\right] } = { 2\pi \cdot \pi = 2 { \pi ^2 } . } $