Вычисление двойного интеграла
Двойной интеграл вычисляется переходом к повторному. Рассмотрим ряд примеров.
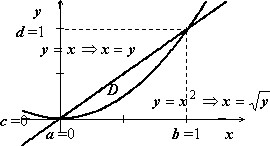
Пример 1
$I=\iint\limits_D { (x+y)dxdy, } \quad D:\left[ { \begin{array} { l } y=x, \\ y=x^2 \\ \end{array} } \right..$
Здесь область $\mathbf { \textit { D } } $ { которую обязательно надо изобразить на чертеже } правильна в направлении обеих осей, поэтому вычисления по обеим формулам перехода имеют одинаковую трудоёмкость:
$ I=\iint\limits_D { (x+y)dxdy } =\int\limits_0^1 { dx\int\limits_ { x^2 } ^x { (x+y)dy } } =\int\limits_0^1 dx\left. { \left( { xy+\frac { y^2 } { 2 } }\right) }\right|_ { x^2 } ^x = \\ =\int\limits_0^1 { \left[ { \left( { \frac { y } { 2 } +y\sqrt y }\right)-\left( { \frac { y^2 } { 2 } +y^2 }\right) }\right]dy } = \int\limits_0^1 { \left( { \frac { y } { 2 } +y^ { 3/2 } -\frac { 3 } { 2 } y^2 }\right)dy } =\left. { \left( { \frac { 1 } { 4 } y^2+\frac { 2 } { 5 } y^ { 5/2 } -\frac { 1 } { 2 } y^3 }\right) }\right|_0^1 =\frac { 3 } { 20 } . $
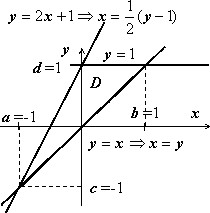
Пример 2
$I=\iint\limits_D { xydxdy, } \quad D:\left[ { \begin{array} { l } y=x,\;y=1, \\ y=2x+1 \\ \end{array} }\right.$.
Здесь область $\mathbf { \textit { D } } $ тоже правильна в направлении обеих осей, однако верхняя граница состоит из двух кусков:
$\varphi _2 (x)=\left[{ \begin{array} { l } 2x+1,\quad -1\leqslant x\leqslant 0; \\ 1,\quad \quad \;\;\;0<x\leqslant 1; \\ \end{array} }\right.$, поэтому первый из повторных интегралов будет содержать два слагаемых:
$I=\iint\limits_D { xydxdy } =\int\limits_ { -1 } ^0 { dx\int\limits_x^ { 2x+1 } { xydy } } +\int\limits_0^1 { dx\int\limits_x^1 { xydy } =\int\limits_ { -1 } ^0 { dx\left. { \left( { x\frac { y^2 } { 2 } }\right) }\right|_x^ { 2x+1 } } + } $ $ +\int\limits_0^1 { dx\left. { \left( { x\frac { y^2 } { 2 } }\right) }\right| } _x^1 =\int\limits_ { -1 } ^0 { \left( { \frac { 1 } { 2 } x(2x+1)^2-\frac { 1 } { 2 } x^3 }\right)dx } +\int\limits_0^1 { \left( { \frac { 1 } { 2 } x-\frac { 1 } { 2 } x^3 }\right)dx } = $ $ =\int\limits_ { -1 } ^0 { \left( { \frac { 3 } { 2 } x^3+2x^2+\frac { 1 } { 2 } x }\right)dx } +\left. { \left( { \frac { 1 } { 4 } x^2-\frac { 1 } { 8 } x^4 }\right) }\right|_0^1 =\left. { \left( { \frac { 3 } { 8 } x^4+\frac { 2 } { 3 } x^3+\frac { 1 } { 4 } x^2 }\right) }\right|_ { -1 } ^0 +\frac { 1 } { 8 } =\frac { 1 } { 8 } -\left( { \frac { 3 } { 8 } -\frac { 2 } { 3 } +\frac { 1 } { 4 } }\right)=\frac { 1 } { 6 } ; $ $ \begin{array} { l } I=\iint\limits_D { xydxdy } =\int\limits_ { -1 } ^1 { dy\int\limits_ { \frac { y-1 } { 2 } } ^y { xydx } } =\int\limits_ { -1 } ^1 { dy\left. { \left( { y\frac { x^2 } { 2 } }\right) }\right|_ { \frac { y-1 } { 2 } } ^y } =\int\limits_ { -1 } ^1 { dy\left( { \frac { y^3 } { 2 } -\frac { y } { 2 } \cdot \left( { \frac { y-1 } { 2 } }\right)^2 }\right) } =\int\limits_ { -1 } ^1 { \left( { \frac { y^3 } { 2 } -\frac { y^3 } { 8 } +\frac { y^2 } { 4 } -\frac { y } { 8 } }\right)dy } = \\ =\left. { \left( { \frac { 3 } { 32 } y^4+\frac { y^3 } { 12 } -\frac { y^2 } { 16 } }\right) }\right|_ { -1 } ^1 =\left( { \frac { 3 } { 32 } +\frac { 1 } { 12 } -\frac { 1 } { 16 } }\right)-\left( { \frac { 3 } { 32 } -\frac { 1 } { 12 } -\frac { 1 } { 16 } }\right)=\frac { 1 } { 6 } . \\ \end{array} $ $y=\sqrt x \Rightarrow x=y^2$
Этот пример проще решается по второй формуле.
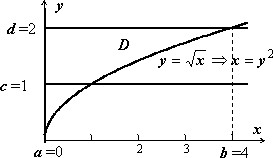
Пример 3
$I=\iint\limits_D { e^ { \frac { x } { y } } dxdy, } \quad D:\left[{ \begin{array} { l } x=0,\;y=\sqrt x , \\ y=1,\;y=2. \\ \end{array} }\right.$.
Здесь переход к повторному интегралу по формуле $I=\iint\limits_D { e^ { \frac { x } { y } } dxdy } =\int\limits_0^1 { dx\int\limits_1^2 { e^ { \frac { x } { y } } dy } } +\int\limits_1^4 { dx\int\limits_ { \sqrt x } ^2 { e^ { \frac { x } { y } } dy } } $ бессмысленен, так как внутренний интеграл не берётся, в то же время второй повторный интеграл вычисляется без проблем: $ I=\iint\limits_D { e^ { \frac { x } { y } } dxdy } =\int\limits_1^2 { dy\int\limits_0^ { y^2 } { e^ { \frac { x } { y } } dx } } =\int\limits_1^2 { dy\int\limits_0^ { y^2 } { ye^ { \frac { x } { y } } d\left( { \frac { x } { y } }\right) } } =\int\limits_1^2 { y\left. { e^ { \frac { x } { y } } }\right|_0^ { y^2 } dy } =\int\limits_1^2 { y\left( { e^y-1 }\right)dy } =\int\limits_1^2 { yde^y } -\left. { \frac { 1 } { 2 } y^2 }\right|_1^2 = $ $ =\left. { \left( { ye^y-e^y }\right) }\right|_1^2 -3/2=e^2-3/2. $ $ y=-\sqrt { 2ax-x^2 } x=a-\sqrt { a^2-y^2 } x=a+\sqrt { a^2-y^2 } $
Пример 4
$I=\iint\limits_D { \sqrt { 4a^2-x^2-y^2 } dxdy, } \quad D:\left[{ x^2+y^2=2ax. }\right.$
Здесь область $\mathbf { \textit { D } } $ ограничена окружностью радиуса $\mathbf { \textit { а } } $, сдвинутой на $\mathbf { \textit { а } } $ единиц по оси $\mathbf { \textit { Ох } } $. Уравнения для правой, левой, верхней и нижней полуокружностей приведены на рисунке. Повторные интегралы в декартовых координатах
$I=\int\limits_0^ { 2a } { dx } \int\limits_ { -\sqrt { 2ax-x^2 } } ^ { \sqrt { 2ax-x^2 } } { \sqrt { 4a^2-x^2-y^2 } dy } , \quad I=\int\limits_ { -a } ^a { dy } \int\limits_ { a-\sqrt { a^2-y^2 } } ^ { a+\sqrt { a^2-y^2 } } { \sqrt { 4a^2-x^2-y^2 } dx } $ можно вычислить, но это достаточно трудоёмко. Попробуем перейти к полярным координатам { это имеет смысл, так как и подынтегральная функция, и кривая, ограничивающая $\mathbf { \textit { D } } $ зависят от выражения $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } =\mathbf { \textit { r } } ^ { 2 } )$. Переход к полярным координатам в уравнении окружности даёт $r^2=2ar\cos \varphi $, или $r=2a\cos \varphi $. Это и есть уравнение границы в полярных координатах. Итак, $\begin{array} { l } I=\iint\limits_D { \sqrt { 4a^2-x^2-y^2 } dxdy } =\iint\limits_ { D_ { r,\varphi } } { \sqrt { 4a^2-r^2 } rdrd\varphi } =\int\limits_ { -\pi /2 } ^ { \pi /2 } { d\varphi \int\limits_0^ { 2a\cos \varphi } { \sqrt { 4a^2-r^2 } rdr } } = \\ =-\frac { 1 } { 2 } \cdot \frac { 2 } { 3 } \int\limits_ { -\pi /2 } ^ { \pi /2 } { \left. { \left( { 4a^2-r^2 }\right)^ { 3/2 } }\right|_0^ { 2a\cos \varphi } d\varphi } =-\frac { 1 } { 3 } \int\limits_ { -\pi /2 } ^ { \pi /2 } { 8a^3\left[ { \left( { 1-\cos ^2\varphi }\right)^ { 3/2 } -1 }\right]d\varphi } =\frac { 8a^3 } { 3 } \left[ { \left. \varphi \right|_ { -\pi /2 } ^ { \pi /2 } -\int\limits_ { -\pi /2 } ^ { \pi /2 } { \sin ^3\varphi d\varphi } }\right]= \\ =\frac { 8 } { 3 } a^3\left. { \left( { \pi +\cos \varphi -\frac { \cos 3\varphi } { 3 } }\right) }\right|_ { -\pi /2 } ^ { \pi /2 } =\frac { 8 } { 3 } \pi a^3. \\ \end{array} $
Ответ явно неправильный. Мы должны получить объём тела, расположенного в полупространстве $z\geqslant 0$, ограниченного цилиндром
$\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } $ = 2$\mathbf { \textit { ax } } $ и сферой $z=\sqrt { 4a^2=x^2-y^2 } $ радиуса 2$\mathbf { \textit { a } } $ сверху; в то время как получили половину объём верхнего полушара { рисунок справа } . С такой ситуацией мы уже встречались, когда рассматривали приложения определённого интеграла. Ошибка делается, когда выражение $\sqrt { 1-\cos ^2\varphi } $ заменяется на $\sin \varphi $, а не на $\vert \sin \varphi \vert $. Дальше необходимо отдельно рассматривать интервалы $-\pi /2\leqslant \varphi \leqslant 0$ и $0\leqslant \varphi \leqslant \pi /2$. Избежать это можно, если воспользоваться симметрией и области, и подынтегральной функции относительно оси $\mathbf { \textit { Ох } } $, т.е. вычислять удвоенный интеграл по половине круга $y\geqslant 0$:
$ \begin{array} { l } I=\iint\limits_D { \sqrt { 4a^2-x^2-y^2 } dxdy } =\iint\limits_ { D_ { r,\varphi } } { \sqrt { 4a^2-r^2 } rdrd\varphi } =2\int\limits_0^ { \pi /2 } { d\varphi \int\limits_0^ { 2a\cos \varphi } { \sqrt { 4a^2-r^2 } rdr } } = \\ =-\frac { 2 } { 3 } \int\limits_0^ { \pi /2 } { \left. { \left( { 4a^2-r^2 }\right)^ { 3/2 } }\right|_0^ { 2a\cos \varphi } d\varphi } =\frac { 16 } { 3 } a^3\left[ { \frac { \pi } { 2 } +\cos \varphi -\frac { \cos 3\varphi } { 3 } }\right]_0^ { \pi /2 } =\frac { 16 } { 3 } a^3\left( { \frac { \pi } { 2 } -\frac { 2 } { 3 } }\right). \\ \end{array} $
Далее:
Класс $S$. Теорема о замкнyтости класса $S$
Вычисление площади поверхности
Определение двойного интеграла
Примеры применения цилиндрических и сферических координат
Булевы функции от $n$ переменных
Свойства криволинейного интеграла второго рода
Класс $T_1$. Теорема о замкнутости класса $T_1$
Механические приложения двойного интеграла
Логические операции над высказываниями
Вычисление двойного интеграла
Несобственные интегралы от неограниченной функции
Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности
Критерий полноты {формулировка}. Лемма о немонотонной функции
Несобственные интегралы по неограниченной области
Огравление $\Rightarrow $
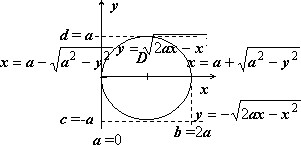
Комментарии ()