Булевы функции от $n$ переменных
Дадим два эквивалентных определения булевой функции.
Определение 1. Функцию $f (x_1, x_2, … , x_n)$ назовем булевой, если она сама и ее аргументы принимают значения 0 и 1.
Определение 2. Булевой функцией $f(x_1, x_2, … , x_n)$ назовем однозначное отображение булева пространства $B^n$ в булево множество $B$, то есть $f : B^n\rightarrow B$.
Пример. Булева функция двух аргументов, принимающая на наборах $01$ и $11$ значение $0$, а на наборах $00$ и $10$ значение $1$:
Определение. Булевы функции равны, $f_1(x_1, …, x_n) = f_2(x_1, …, x_n)$, если на одинаковых наборах они принимают одинаковые значения.
Число булевых функций от $n$ переменных равно $2^ { 2^ { n } } $
Пример 1. Число булевых функций от $n = 1$ переменной равно $2^ { 2^ { n } } = 2^ { 2^ { 1 } } = 2^ { 2 } = 4$. Это $0, 1, x$ и $\bar { x } $
Пример 2. Число булевых функций от $n = 2$ переменных равно $2^ { 2^ { n } } = 2^ { 2^ { 2 } } = 2^ { 4 } = 16$. Они все указаны в таблице
| $x_1$ | $x_2$ | $f_1$ | $f_2$ | $f_3$ | $f_4$ | $f_5$ | $f_6$ | $f_7$ | $f_8$ | $f_9$ | $f_ { 10 } $ | $f_ { 11 } $ | $f_ { 12 } $ | $f_ { 13 } $ | $f_ { 14 } $ | $f_ { 15 } $ | $f_ { 16 } $ |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
У некоторых функций есть специальные названия.
$f_1(x_1, x_2) = 0$ - тождественный нуль;
$f_2(x_1, x_2) = x_1\And x_2$ - конъюнкция. Очень часто знак $\And $ опускают и пишут просто $x_1x_2$;
$f_7(x_1, x_2) = x_1\oplus x_2$ - сложение по модулю 2;
$f_8(x_1, x_2) = x_1\vee x_2$ - дезъюнкция;
$f_9(x_1, x_2) = x_1\downarrow x_2$ - стрелка Пирса;
$f_ { 10 } (x_1, x_2) = x_1\equiv x_2$ - эквиваленция;
$f_ { 14 } (x_1, x_2) = x_1\rightarrow x_2$ - импликация;
$f_ { 15 } (x_1, x_2) = x_1|x_2$ - штрих Шеффера;
$f_ { 16 } (x_1, x_2) = 1$ - тождественная единица.
Далее:
Введение
Класс $T_0$. Теорема о замкнутости класса $T_0$
Соленоидальное векторное поле
Теорема Стокса
Дифференциальные характеристики векторного поля
Свойства криволинейного интеграла второго рода
Теорема о полныx системаx в Pk
Инвариантное определение дивергенции
Замена переменных в тройном интеграле
Определение тройного интеграла. Теорема существования тройного интеграла
Формула Грина
Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Вычисление криволинейного интеграла первого рода. Примеры
Класс Te . Теорема о замкнутости Te
Булевы функции от $n$ переменных
Огравление $\Rightarrow $
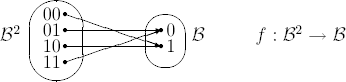
Комментарии ()