Примеры применения цилиндрических и сферических координат

Как и в случае перехода к полярным координатам в двойном интеграле, дать однозначный рецепт того, когда следует применять цилиндрические или сферические координаты, нельзя, это дело опыта. Можно попробовать применить цилиндрические координаты, если подынтегральная функция и/или уравнения поверхностей, ограничивающих объём $\mathbf { \textit { V } } $, зависят от комбинации $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } =\mathbf { \textit { r } } ^ { 2 } $; сферические - если эти уравнения зависят от $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } =\mathbf { \textit { r } } ^ { 2 } $. Рассмотрим ряд примеров.

Пример 1

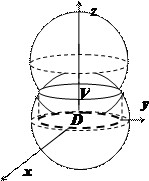
Найти объём $\mathbf { \textit { V } } $ общей части двух шаров, ограниченных сферами

$\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } =\mathbf { \textit { R } } ^ { 2 } $, $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } $ = 2$\mathbf { \textit { Rz } } ^ { } $.

Решение:

Пересечение сфер находится на уровне $2Rz=R^2\Rightarrow z=R/2$ и представляет собой круг радиуса $R\frac { \sqrt 3 } { 2 } $. Объём $\mathbf { \textit { V } } $ограничен сверху поверхностью $z=\sqrt { R^2-x^2-y^2 } $, снизу - поверхностью $z=R-\sqrt { R^2-x^2-y^2 } $. Вычисления в декартовых координатах дают $V=\iiint\limits_V { dv } =\iiint\limits_V { dxdydz } =\int\limits_ { -R\frac { \sqrt 3 } { 2 } } ^ { R\frac { \sqrt 3 } { 2 } } { dx\int\limits_ { -\sqrt { \frac { 3 } { 4 } R^2-x^2 } } ^ { \sqrt { \frac { 3 } { 4 } R^2-x^2 } } { dy\int\limits_ { R-\sqrt { R^2-x^2-y^2 } } ^ { \sqrt { R^2-x^2-y^2 } } { dz } } } $ - достаточно громоздкие выкладки.

В цилиндрических координатах объём $\mathbf { \textit { V } } $ ограничен сверху поверхностью $z=\sqrt { R^2-r^2 } $, снизу - поверхностью $z=R-\sqrt { R^2-r^2 } $, поэтому

$V=\iiint\limits_V { dv } =\iiint\limits_V { rdrd\varphi dz } =\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { R\frac { \sqrt 3 } { 2 } } { rdr\int\limits_ { R-\sqrt { R^2-r^2 } } ^ { \sqrt { R^2-r^2 } } { dz } } } =2\pi \int\limits_0^ { R\frac { \sqrt 3 } { 2 } } { \left[ { 2\sqrt { R^2-r^2 } -R }\right]rdr } =$ $ =2\pi \left. { \left[ { -\frac { 2 } { 3 } \sqrt { \left( { R^2-r^2 }\right)^3 } -R\frac { r^2 } { 2 } }\right] }\right|_0^ { R\frac { \sqrt 3 } { 2 } } =2\pi \left[ { \frac { 2 } { 3 } R^3-\frac { 2 } { 3 } \sqrt { \left( { R^2/4 }\right)^3 } -\frac { 3R^3 } { 8 } }\right]=2\pi R^3\left( { \frac { 2 } { 3 } -\frac { 2 } { 24 } -\frac { 3 } { 8 } }\right)=\frac { 5 } { 12 } \pi R^3. $

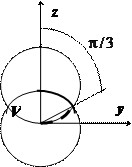
В сферических координатах уравнение нижней сферы принимает вид $r=R$, верхней - $r^2=2Rr\cos \theta \Rightarrow r=2R\cos \theta $, их пересечение соответствует значению $\cos \theta =1/2\Rightarrow \theta =\pi /3$. В интервале $0\leqslant \theta \leqslant \pi /3 \quad \mathbf { \textit { r } } $ меняется от $0$ до $\mathbf { \textit { R } } $, в интервале $\pi /3\leqslant \theta \leqslant \pi /2 \quad \mathbf { \textit { r } } $ меняется от $0$ до $2R\cos \theta $, поэтому

$V=\iiint\limits_V { dv } =\iiint\limits_V { r^ { 2 } \sin\theta drd\varphi d\theta } = \int_0^ { 2\pi } d \phi \int_0^ { \pi/3 } \sin \theta d\theta \int_0^R r^2 dr + \int_0^ { 2\pi } d \phi \int_ { \pi/3 } ^ { \pi/2 } \sin \theta d\theta \int_0^ { 2R\cos \theta } r^2 dr = 2\pi \frac { R^3 } { 3 } (-\cos\theta) =\\ =2\pi \frac { R^3 } { 3 } \left. { \left( { -\cos \theta }\right) }\right|_0^ { \frac { \pi } { 3 } } +2\pi \frac { 8R^3 } { 3 } \int\limits_ { \frac { \pi } { 3 } } ^ { \frac { \pi } { 2 } } { \cos ^3\theta \sin \theta d\theta } =\frac { \pi R^3 } { 3 } -\frac { 16\pi R^3 } { 3 } \cdot \left. { \frac { \cos ^4\theta } { 4 } }\right|_ { \frac { \pi } { 3 } } ^ { \frac { \pi } { 2 } } = $ $ =\frac { \pi R^3 } { 3 } +\frac { \pi R^3 } { 3\cdot 4 } =\frac { 5\pi R^3 } { 12 } . $

В этом примере трудоёмкость вычислений в цилиндрических и сферических координатах примерно одинакова.

Пример 2

$I=\iiint\limits_V { (x+y+z)dxdydz } ;\quad V:\left[{ \begin{array} { l } x=2-y^2-z^2, \\ x^2=y^2+z^2,\;x\geqslant 0. \\ \end{array} }\right.$

Решение:

Параболоид и конус пересекаются в плоскости $x=2-x^2\Rightarrow x=1$ по кругу радиуса 1. Осью симметрии объёма $\mathbf { \textit { V } } $ служит ось $\mathbf { \textit { Ох } } $, поэтому цилиндрические координаты вводим формулами $x=x,\quad y=r\cos \varphi ,\quad z=r\sin \varphi ; \quad I=\iiint\limits_V { (x+y+z)dxdydz } =\iiint\limits_V { (x+r\cos \varphi +r\sin \varphi )rdxdrd\varphi } =\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^1 { rdr\int\limits_r^ { 2-r^2 } { (x+r\cos \varphi +r\sin \varphi )dx } } } =$ $ =\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^1 { \left. { \frac { x^2 } { 2 } }\right|_r^ { 2-r^2 } rdr } } +\int\limits_0^ { 2\pi } { (\cos \varphi +\sin \varphi )d\varphi \int\limits_0^1 { \left. x \right|_r^ { 2-r^2 } r^2dr } } =\pi \int\limits_0^1 { \left( { 4-5r^2+r^4 }\right)dr } =\frac { 38\pi } { 15 } . $ Применение сферических координат в этом примере нецелесообразно { громоздкое уравнение для параболоида } .

Пример 3

$I=\iiint\limits_V { \sqrt { x^2+y^2+z^2 } dxdydz } ;\quad V:\left[{ x^2+y^2+z^2=z. }\right.$

Решение:

Здесь область интегрирования - шар радиуса 1/2, сдвинутый по оси $\mathbf { \textit { Оz } } $ на 1/2 единицы, подынтегральная функция зависит от выражения $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } $, поэтому применим сферические координаты. Уравнение сферы $x^2+y^2+z^2=z\Rightarrow r^2=r\cos \theta \Rightarrow r=\cos \theta \left( { \Rightarrow 0\leqslant \theta \leqslant \pi /2 }\right)$ , поэтому $I=\iiint\limits_V { \sqrt { x^2+y^2+z^2 } dxdydz } =\iiint\limits_V { r\cdot r^2\sin \theta drd\varphi d\theta } =\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { \pi /2 } { \sin \theta d\theta } \int\limits_0^ { \cos \theta } { r^3dr } } =\frac { 2\pi } { 4 } \int\limits_0^ { \pi /2 } { \left. { r^4 }\right|_0^ { \cos \theta } \sin \theta d\theta } = \\ =\frac { 2\pi } { 4 } \int\limits_0^ { \pi /2 } { \cos ^4\theta \sin \theta d\theta } =-\frac { 2\pi } { 4\cdot 5 } \left. { \cos ^5\theta }\right|_0^ { \pi /2 } =\frac { \pi } { 10 } $.

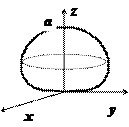
Пример 4

Вычислить объём тела, ограниченного поверхностью $\left( { x^2+y^2+z^2 }\right)^ { \,2 } =a^3z,\;a=const>0$

Решение:

Здесь тоже для того, чтобы понять, как устроено тело, и найти его объём, надо перейти к сферическим координатам { на это указывает комбинация $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } =\mathbf { \textit { r } } ^ { 2 } )$. Уравнение поверхности $\left( { x^2+y^2+z^2 }\right)^ { \,2 } =a^3z\Rightarrow r^4=a^3r\cos \vartheta \Rightarrow r=a\sqrt[3] { \cos \vartheta } \;\left( { \Rightarrow 0\leqslant \theta \leqslant \pi /2 }\right)$. По этому уравнению поверхность построить уже можно; отсутствие координаты $\varphi $ в уравнении показывает, что это - тело вращения вокруг оси $\mathbf { \textit { Oz } } $. Находим объём: $ V=\iiint\limits_V { r^2\sin \theta drd\varphi d\theta } =\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { \pi /2 } { \sin } } \theta d\theta \int\limits_0^ { a\sqrt[3] { \cos \theta } } { r^2dr } =\frac { 2\pi } { 3 } \int\limits_0^ { \pi /2 } { \left. { r^3 }\right|_0^ { a\sqrt[3] { \cos \theta } } \sin \theta d\theta = } $ $ =\frac { 2\pi a^3 } { 3 } \int\limits_0^ { \pi /2 } { \cos \theta \sin \theta d\theta = } \frac { \pi a^3 } { 3 } . $

Пример 5

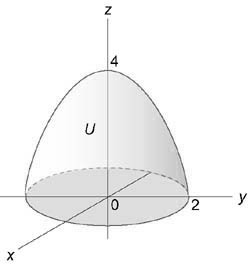
Вычислить интеграл $\iiint\limits_U { \left( { { x^4 } + 2 { x^2 } { y^2 } + { y^4 } }\right)dxdydz } ,$ где область (U) ограничена поверхностью ( { x^2 } + { y^2 } \le 1) и плоскостями (z = 0,) (z = 1).

Решение:

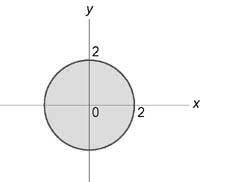
Данный интеграл удобно вычислить в цилиндрических координатах. Проекция области интегрирования на плоскость (Oxy) представляет собой круг ( { x^2 } + { y^2 } \le 1) или (0 \le \rho \le 1).

Заметим, что подынтегральное выражение записывается в виде $ { \left( { { x^4 } + 2 { x^2 } { y^2 } + { y^4 } }\right) } = { { \left( { { x^2 } + { y^2 } }\right)^2 } } = { { \left( { { \rho ^2 } }\right)^2 } = { \rho ^4 } } $

Тогда интеграл будет равен $I = \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } \rho d\rho } \int\limits_0^1 { dz } .$

Здесь во втором интеграле добавлен множитель (\rho) якобиан преобразования декартовых координат в цилиндрические. Все три интеграла по каждой из переменной не зависят друг от друга.

В результате тройной интеграл легко вычисляется: $ { I = \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } \rho d\rho } \int\limits_0^1 { dz } } = { 2\pi \int\limits_0^1 { { \rho ^5 } d\rho } \int\limits_0^1 { dz } } = { 2\pi \cdot 1 \cdot \int\limits_0^1 { { \rho ^5 } d\rho } } = { 2\pi \left. { \left( { \frac { { { \rho ^6 } } } { 6 } }\right) }\right|_0^1 } = { 2\pi \cdot \frac { 1 } { 6 } = \frac { \pi } { 3 } . } $

Пример 6

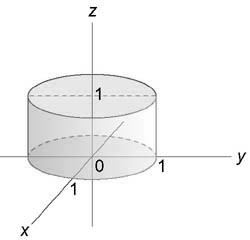
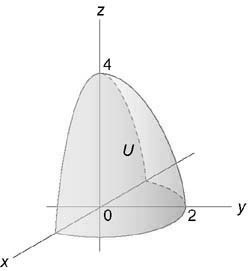
Вычислить интеграл $\iiint\limits_U { \left( { { x^2 } + { y^2 } }\right)dxdydz } ,$ где область (U) ограничена поверхностями ( { x^2 } + { y^2 } = 3z,) (z = 3)

Решение:

Область интегрирования изображена на рисунке

Для вычисления интеграла перейдем к цилиндрическим координатам: $ { x = \rho \cos \varphi , } \;\; { y = \rho \sin \varphi , } \;\; { z = z. } $ Дифференциал при этом равен $dxdydz = \rho d\rho d\varphi dz\;\;\left( { \rho - \text { якобиан } }\right).$

Уравнение параболической поверхности принимает вид: $ { \rho ^2 } { \cos ^2 } \varphi + { \rho ^2 } { \sin^2 } \varphi = 3z\;\;\text { или } \;\; { \rho ^2 } = 3z.$ Проекция области интегрирования (U) на плоскость (Oxy) представляет собой окружность ( { x^2 } + { y^2 } \le 9) радиусом (\rho = 3).

Координата (\rho) изменяется в пределах от (0) до (3,) угол (\varphi) от (0) до (2\pi) и координата (z) от (\large\frac { { { \rho ^2 } } } { 3 } \normalsize) до (3.)

В результате интеграл будет равен $ { I = \iiint\limits_U { \left( { { x^2 } + { y^2 } }\right)dxdydz } } = { \iiint\limits_ { U' } { { \rho ^2 } \cdot \rho d\rho d\varphi dz } } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^3 { { \rho ^3 } d\rho } \int\limits_ { \frac { { { \rho ^2 } } } { 3 } } ^3 { dz } } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^3 { { \rho ^3 } d\rho } \cdot \left[ { \left. z \right|_ { \frac { { { \rho ^2 } } } { 3 } } ^3 }\right] } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^3 { { \rho ^3 } \left( { 3 - \frac { { { \rho ^2 } } } { 3 } }\right)d\rho } } = \\ = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^3 { \left( { 3 { \rho ^3 } - \frac { { { \rho ^5 } } } { 3 } }\right)d\rho } } = { \int\limits_0^ { 2\pi } { d\varphi } \cdot \left[ { \left. { \left( { \frac { { 3 { \rho ^4 } } } { 4 } - \frac { { { \rho ^6 } } } { { 18 } } }\right) }\right|_0^3 }\right] } = { \left( { \frac { { 3 \cdot 81 } } { 4 } - \frac { { 729 } } { { 18 } } }\right)\int\limits_0^ { 2\pi } { d\varphi } } = { \frac { { 81 } } { 4 } \cdot 2\pi = \frac { { 81\pi } } { 2 } . } $

Пример 7

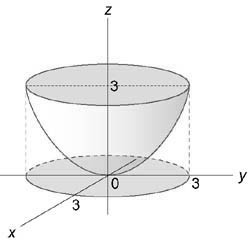
Используя цилиндрические координаты, найти значение интеграла $ I = \int\limits_ { - 2 } ^2 { dx } \int\limits_ { - \sqrt { 4 - { x^2 } } } ^ { \sqrt { 4 - { x^2 } } } { dy } \int\limits_0^ { 4 - { x^2 } - { y^2 } } { { y^2 } dz } $

Решение:

Область интегрирования (U) изображена на рисунке:

Ее проекция на плоскость (Oxy) представляет собой круг ( { x^2 } + { y^2 } = { 2^2 } ):

Новые переменные в цилиндрических координатах будут изменяться в пределах $ { 0 \le \rho \le 2, } \;\; { 0 \le \varphi \le 2\pi , } \;\; { 0 \le z \le 4 - { \rho ^2 } . } $

Подставляя (x = \rho \cos \varphi ) и (x = \rho \sin \varphi,) найдем значение интеграла: $ { I = \int\limits_ { - 2 } ^2 { dx } \int\limits_ { - \sqrt { 4 - { x^2 } } } ^ { \sqrt { 4 - { x^2 } } } { dy } \int\limits_0^ { 4 - { x^2 } - { y^2 } } { { y^2 } dz } } = { \iiint\limits_U { { y^2 } dxdydz } } = { \iiint\limits_ { U' } { { { \left( { \rho \sin \varphi }\right) } ^2 } \rho d\rho d\varphi dz } } = { \iiint\limits_ { U' } { { \rho ^3 } { { \sin } ^2 } \varphi d\rho d\varphi dz } } = { \int\limits_0^ { 2\pi } { { { \sin } ^2 } \varphi d\varphi } \int\limits_0^2 { { \rho ^3 } \left( { 4 - { \rho ^2 } }\right)d\rho } } = \\ = { \int\limits_0^ { 2\pi } { { { \sin } ^2 } \varphi d\varphi } \int\limits_0^2 { \left( { 4 { \rho ^3 } - { \rho ^5 } }\right)d\rho } } = { \int\limits_0^ { 2\pi } { { { \sin } ^2 } \varphi d\varphi } \cdot \left[ { \left. { \left( { \frac { { 4 { \rho ^4 } } } { 4 } - \frac { { { \rho ^6 } } } { 6 } }\right) }\right|_0^2 }\right] } = { \left( { { 2^4 } - \frac { { { 2^6 } } } { 6 } }\right)\int\limits_0^ { 2\pi } { { { \sin } ^2 } \varphi d\varphi } } = { \frac { { 16 } } { 3 } \int\limits_0^ { 2\pi } { { { \sin } ^2 } \varphi d\varphi } } = { \frac { { 16 } } { 3 } \int\limits_0^ { 2\pi } { \frac { { 1 - \cos 2\varphi } } { 2 } d\varphi } } = \\ = { \frac { 8 } { 3 } \int\limits_0^ { 2\pi } { \left( { 1 - \cos 2\varphi }\right)d\varphi } } = { \frac { 8 } { 3 } \left[ { \left. { \left( { \varphi - \frac { { \sin 2\varphi } } { 2 } }\right) }\right|_0^ { 2\pi } }\right] } = { \frac { 8 } { 3 } \cdot 2\pi = \frac { { 16\pi } } { 3 } . } $

Пример 8

Вычислить интеграл, используя цилиндрические координаты: $\iiint\limits_U { \sqrt { { x^2 } + { y^2 } } dxdydz } .$ Область (U) ограничена параболоидом (z = 4 - { x^2 } - { y^2 } ,) цилиндром ( { x^2 } + { y^2 } = 4) и плоскостями (y = 0,) (z = 0)

Решение:

Изобразив схематически область интегрирования (U,) находим, что ее проекция на плоскость (Oxy) { область (D) } представляет собой полукруг радиусом (\rho = 2).

Перейдем к цилиндрическим координатам, применяя подстановки $ { x = \rho \cos \varphi , } \;\; { y = \rho \sin \varphi , } \;\; { z = z, } \;\; { dxdydz = \rho d\rho d\varphi dz. } $

Новые переменные будут изменяться в пределах $ { 0 \le \rho \le 2, } \;\; { 0 \le \varphi \le \pi , } \;\; { 0 \le z \le 4 - { \rho ^2 } . } $

Теперь вычисляем интеграл: $ { I = \iiint\limits_U { \sqrt { { x^2 } + { y^2 } } dxdydz } } = { \iiint\limits_ { U' } { \rho \cdot \rho d\rho d\varphi dz } } = { \iiint\limits_ { U' } { { \rho ^2 } d\rho d\varphi dz } } = { \int\limits_0^\pi { d\varphi } \int\limits_0^2 { { \rho ^2 } d\rho } \int\limits_0^ { 4 - { \rho ^2 } } { dz } } = { \int\limits_0^\pi { d\varphi } \int\limits_0^2 { { \rho ^2 } d\rho } \cdot \left[ { \left. z \right|_0^ { 4 - { \rho ^2 } } }\right] } = { \int\limits_0^\pi { d\varphi } \int\limits_0^2 { { \rho ^2 } \left( { 4 - { \rho ^2 } }\right)d\rho } } = \\ = { \int\limits_0^\pi { d\varphi } \int\limits_0^2 { \left( { 4 { \rho ^2 } - { \rho ^4 } }\right)d\rho } } = { \int\limits_0^\pi { d\varphi } \left[ { \left. { \left( { \frac { { 4 { \rho ^3 } } } { 3 } - \frac { { { \rho ^5 } } } { 5 } }\right) }\right|_0^2 }\right] } = { \left( { \frac { 4 } { 3 } \cdot { 2^3 } - \frac { { { 2^5 } } } { 5 } }\right)\int\limits_0^\pi { d\varphi } } = { \frac { { 64 } } { { 15 } } \int\limits_0^\pi { d\varphi } } = { \frac { { 64 } } { { 15 } } \cdot \left[ { \left. \varphi \right|_0^\pi }\right] = \frac { { 64\pi } } { { 15 } } . } $

Пример 9

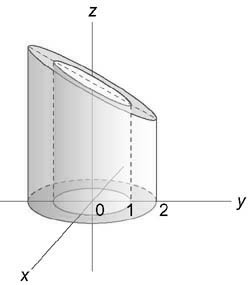
Найти интеграл $\iiint\limits_U { ydxdydz } ,$ где область (U) ограничена плоскостями (z = x + 1,) (z = 0) и цилиндрическими поверхностями ( { x^2 } + { y^2 } = 1,) ( { x^2 } + { y^2 } = 4)

Решение:

Вычислим данный интеграл в цилиндрических координатах. Из условия $0 \le z \le x + 1$ следует, что $0 \le z \le \rho \cos \varphi + 1.$ Область интегрирования в плоскости (Oxy) представляет собой кольцо, ограниченное окружностями ( { x^2 } + { y^2 } = 1) и ( { x^2 } + { y^2 } = 4)

Следовательно, переменные (\rho) и (\varphi) изменяются в интервале $1 \le \rho \le 2,\;\;0 \le \varphi \le 2\pi .$

Находим интеграл: $ { I = \iiint\limits_U { ydxdydz } } = { \iiint\limits_ { U' } { \rho \sin \varphi \cdot \rho d\rho d\varphi dz } } = { \iiint\limits_ { U' } { { \rho ^2 } \sin \varphi d\rho d\varphi dz } } = { \int\limits_0^ { 2\pi } { \sin \varphi d\varphi } \int\limits_0^2 { { \rho ^2 } d\rho } \int\limits_0^ { \rho \cos \varphi + 1 } { dz } } = { \int\limits_0^ { 2\pi } { \sin \varphi d\varphi } \int\limits_0^2 { { \rho ^2 } d\rho } \cdot \left[ { \left. z \right|_0^ { \rho \cos \varphi + 1 } }\right] } = \\ = { \int\limits_0^ { 2\pi } { \sin \varphi d\varphi } \int\limits_0^2 { { \rho ^2 } \left( { \rho \cos \varphi + 1 }\right)d\rho } } = { \int\limits_0^ { 2\pi } { \sin \varphi d\varphi } \int\limits_0^2 { \left( { { \rho ^3 } \cos \varphi + { \rho ^2 } }\right)d\rho } } = { \int\limits_0^ { 2\pi } { \sin \varphi d\varphi } \cdot \left[ { \left. { \left( { \frac { { { \rho ^4 } } } { 4 } \cos \varphi + \frac { { { \rho ^3 } } } { 3 } }\right) }\right|_ { \rho = 1 } ^ { \rho = 2 } }\right] } = \\ = { \int\limits_0^ { 2\pi } { \sin \varphi \left[ { \left( { 4\cos \varphi + \frac { 8 } { 3 } }\right) - \left( { \frac { { \cos \varphi } } { 4 } + \frac { 1 } { 3 } }\right) }\right]d\varphi } } = { \int\limits_0^ { 2\pi } { \sin \varphi \left( { \frac { { 15 } } { 4 } \cos \varphi + \frac { 7 } { 3 } }\right)d\varphi } } = { \int\limits_0^ { 2\pi } { \left( { \frac { { 15 } } { 4 } \sin \varphi \cos \varphi + \frac { 7 } { 3 } \sin \varphi }\right)d\varphi } } = \\ = { \int\limits_0^ { 2\pi } { \left( { \frac { { 15 } } { 8 } \sin 2\varphi + \frac { 7 } { 3 } \sin \varphi }\right)d\varphi } } = { \left. { \left( { - \frac { { 15 } } { { 16 } } \cos 2\varphi - \frac { 7 } { 3 } \cos \varphi }\right) }\right|_0^ { 2\pi } = 0. } $

Этот результат закономерен, поскольку область (U) симметрична относительно плоскости (Oxz,) а подынтегральная функция является четной.

Пример 10

Найти интеграл (\iiint\limits_U { \sqrt { { x^2 } + { y^2 } + { z^2 } } dxdydz } ,) где область интегрирования (U) шар, заданный уравнением ( { { x^2 } + { y^2 } + { z^2 } } = 25.)

Решение:

Поскольку область (U) представляет собой шар, и к тому же подынтегральное выражение является функцией, зависящей от $f\left( { { x^2 } + { y^2 } + { z^2 } }\right),$ то перейдем к сферическим координатам.

Сделаем замену: $ { x = \rho \cos \varphi \sin \theta , } \;\; { y = \rho \sin \varphi \sin \theta , } \;\; { z = \rho \cos \theta , } $ Новые переменные изменяются в пределах: $ { 0 \le \rho \le 5, } \;\; { 0 \le \varphi \le 2\pi , } \;\; { 0 \le \theta \le \pi . } $

Учитывая якобиан ( { \rho ^2 } \sin \theta,) записываем интеграл в виде: $ { I = \iiint\limits_U { \sqrt { { x^2 } + { y^2 } + { z^2 } } dxdydz } } = { \iiint\limits_ { U' } { \rho \cdot { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^5 { { \rho ^3 } d\rho } \int\limits_0^\pi { \sin \theta d\theta } } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^5 { { \rho ^3 } d\rho } \left[ { \left. { \left( { - \cos \theta }\right) }\right|_0^\pi }\right] } = \\ = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^5 { { \rho ^3 } d\rho } \left( { - \cos \pi + \cos 0 }\right) } = { 2\int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^5 { { \rho ^3 } d\rho } } = { 2\int\limits_0^ { 2\pi } { d\varphi } \cdot \left[ { \left. { \left( { \frac { { { \rho ^4 } } } { 4 } }\right) }\right|_0^5 }\right] } = \\ = { 2\int\limits_0^ { 2\pi } { d\varphi } \cdot \frac { { { 5^4 } } } { 4 } } = { \frac { { 625 } } { 2 } \int\limits_0^ { 2\pi } { d\varphi } } = { \frac { { 625 } } { 2 } \cdot 2\pi = 625\pi . } $

Пример 11

Вычислить интеграл $\iiint\limits_U { { e^ { { { \left( { { x^2 } + { y^2 } + { z^2 } }\right) } ^ { \frac { 3 } { 2 } } } } } dxdydz } ,$ где область (U) представляет собой единичный шар ( { { x^2 } + { y^2 } + { z^2 } } \le 1.)

Решение:

Центр данного шара расположен в начале координат. Следовательно, в сферических координатах область интегрирования (U) описывается неравенствами $ { 0 \le \rho \le 1, } \;\; { 0 \le \varphi \le 2\pi , } \;\; { 0 \le \theta \le \pi . } $

Записывая интеграл в сферических координатах, получаем $ { I = \iiint\limits_U { { e^ { { { \left( { { x^2 } + { y^2 } + { z^2 } }\right) } ^ { \frac { 3 } { 2 } } } } } dxdydz } } = { \iiint\limits_ { U' } { { e^ { { { \left( { { \rho ^2 } }\right) } ^ { \frac { 3 } { 2 } } } } } { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = { \iiint\limits_ { U' } { { e^ { { \rho ^3 } } } { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { e^ { { \rho ^3 } } } { \rho ^2 } d\rho } \int\limits_0^\pi { \sin \theta d\theta } . } $

Как видно, тройной интеграл вырождается в произведение трех однократных интегралов, каждый из которых вычисляется независимо. В результате находим $ { I = \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { e^ { { \rho ^3 } } } { \rho ^2 } d\rho } \int\limits_0^\pi { \sin \theta d\theta } } = { \left[ { \left. \varphi \right|_0^ { 2\pi } }\right] \cdot \int\limits_0^1 { \left( { { e^ { { \rho ^3 } } } \cdot \frac { 1 } { 3 } d { \rho ^3 } }\right) } \cdot \left[ { \left. { \left( { - \cos \theta }\right) }\right|_0^\pi }\right] } = { 2\pi \cdot \frac { 1 } { 3 } \left[ { \left. { \left( { { e^ { { \rho ^3 } } } }\right) }\right|_ { { \rho ^3 } = 0 } ^ { { \rho ^3 } = 1 } }\right] \cdot \left( { - \cos \pi + \cos 0 }\right) } = { \frac { { 2\pi } } { 3 } \cdot \left( { e - 1 }\right) \cdot 2 } = { \frac { { 4\pi } } { 3 } \left( { e - 1 }\right). } $

Пример 12

Вычислить интеграл (\iiint\limits_U { xyzdxdydz } ,) где область (U) представляет собой часть шара ( { x^2 } + { y^2 } + { z^2 } \le { R^2 } ,) расположенную в первом октанте (x \ge 0, y \ge 0, z \ge 0.)

Решение:

Перейдем к сферическим координатам. Сделаем замену переменных: $ { x = \rho \cos \varphi \sin \theta , } \;\; { y = \rho \sin \varphi \sin \theta , } \;\; { z = \rho \cos \theta , } \;\; { dxdydz = { \rho ^2 } \sin \theta d\rho d\varphi d\theta . } $ Новые переменные будут изменяться в пределах: $ { 0 \le \rho \le R, } \;\; { 0 \le \varphi \le \frac { \pi } { 2 } , } \;\;0 { \le \theta \le \frac { \pi } { 2 } . } $ Тогда интеграл в сферических координатах равен $ { I = \iiint\limits_U { xyzdxdydz } } = { \iiint\limits_ { U' } { \left[ { \rho \cos \varphi \sin \theta \cdot \rho \sin \varphi \sin \theta \cdot \rho \cos \theta \cdot { \rho ^2 } \sin \theta d\rho d\varphi d\theta }\right] } } = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \cos \varphi \sin \varphi d\varphi } \int\limits_0^R { { \rho ^5 } d\rho } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { { { \sin } ^3 } \theta \cos \theta d\theta } } = \\ = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \left( { \frac { 1 } { 2 } \sin 2\varphi d\varphi }\right) } \int\limits_0^R { { \rho ^5 } d\rho } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { { { \sin } ^3 } \theta \cos \theta d\theta } } = \\ = { \frac { 1 } { 2 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin 2\varphi d\varphi } \int\limits_0^R { { \rho ^5 } d\rho } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { { { \sin } ^3 } \theta d\left( { \sin \theta }\right) } } = { \frac { 1 } { 2 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin 2\varphi d\varphi } \int\limits_0^R { { \rho ^5 } d\rho } \cdot \left[ { \left. { \left( { \frac { { { { \sin } ^4 } \theta } } { 4 } }\right) }\right|_ { \theta = \\ = 0 } ^ { \theta = \large\frac { \pi } { 2 } \normalsize } }\right] } = { \frac { 1 } { 8 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin 2\varphi d\varphi } \int\limits_0^R { { \rho ^5 } d\rho } \cdot \left( { { { \sin } ^4 } \frac { \pi } { 2 } - { { \sin } ^4 } 0 }\right) } = \\ = { \frac { 1 } { 8 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin 2\varphi d\varphi } \int\limits_0^R { { \rho ^5 } d\rho } \cdot 1 } = { \frac { 1 } { 8 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin 2\varphi d\varphi } \cdot \left[ { \left. { \left( { \frac { { { \rho ^6 } } } { 6 } }\right) }\right|_0^R }\right] } = { \frac { { { R^6 } } } { { 48 } } \left[ { \left. { \left( { - \frac { { \cos 2\varphi } } { 2 } }\right) }\right|_0^ { \large\frac { \pi } { 2 } \normalsize } }\right] } = { \frac { { { R^6 } } } { { 96 } } \left( { - \cos \pi + \cos 0 }\right) } = { \frac { { { R^6 } } } { { 96 } } \cdot 2 } = { \frac { { { R^6 } } } { { 48 } } . } $

Пример 13

Найти тройной интеграл $\iiint\limits_U { \left( { \frac { { { x^2 } } } { { { a^2 } } } + \frac { { { y^2 } } } { { { b^2 } } } + \frac { { { z^2 } } } { { { c^2 } } } }\right)dxdydz } ,$ где область (U) ограничена эллипсоидом $ { \frac { { { x^2 } } } { { { a^2 } } } + \frac { { { y^2 } } } { { { b^2 } } } + \frac { { { z^2 } } } { { { c^2 } } } } = 1.$

Решение:

Для вычисления интеграла перейдем к обобщенным сферическим координатам путем следующей замены переменных: $ { x = a\rho \cos \varphi \sin \theta , } \;\; { y = b\rho \sin \varphi \sin \theta , } \;\; { z = c\rho \cos \theta . } $ Модуль якобиана данного преобразования равен (\left| I \right| = abc { \rho ^2 } \sin \theta .) Поэтому для дифференциалов справедливо соотношение $dxdydz = abc { \rho ^2 } \sin \theta d\rho d\varphi d\theta .$ В новых координатах интеграл принимает вид: $ { I = \iiint\limits_U { \left( { \frac { { { x^2 } } } { { { a^2 } } } + \frac { { { y^2 } } } { { { b^2 } } } + \frac { { { z^2 } } } { { { c^2 } } } }\right)dxdydz } } = { \iiint\limits_ { U' } { \left[ { \frac { { { { \left( { a\rho \cos \varphi \sin \theta }\right) } ^2 } } } { { { a^2 } } } + \frac { { { { \left( { b\rho \sin \varphi \sin \theta }\right) } ^2 } } } { { { b^2 } } } + \frac { { { { \left( { c\rho \cos \theta }\right) } ^2 } } } { { { c^2 } } } }\right]abc { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = \\ = { \iiint\limits_ { U' } { \left[ { { \rho ^2 } { { \cos } ^2 } \varphi \, { { \sin } ^2 } \theta + { \rho ^2 } { \sin^2 } \varphi \, { { \sin } ^2 } \theta + { \rho ^2 } { { \cos } ^2 } \theta }\right]abc { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = \\ = { \iiint\limits_ { U' } { \left[ { { \rho ^2 } { { \sin } ^2 } \theta \underbrace { \left( { { { \cos } ^2 } \varphi + { \sin^2 } \varphi }\right) } _1 + { \rho ^2 } { { \cos } ^2 } \theta }\right]abc { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = \\ = { \iiint\limits_ { U' } { { \rho ^2 } \underbrace { \left( { { \sin^2 } \theta + { { \cos } ^2 } \theta }\right) } _1abc { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = { abc\iiint\limits_ { U' } { { \rho ^4 } \sin \theta d\rho d\varphi d\theta } . } $

Область интегрирования (U') в сферических координатах представляет собой параллелепипед и определяется неравенствами $ { 0 \le \rho \le 1, } \;\; { 0 \le \varphi \le 2\pi , } \;\; { 0 \le \theta \le \pi . } $ Тогда тройной интеграл становится равным $ { I = abc\iiint\limits_ { U' } { { \rho ^4 } \sin \theta d\rho d\varphi d\theta } } = { abc\int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } d\rho } \int\limits_0^\pi { \sin \theta d\theta } } = { abc\int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } d\rho } \cdot \left[ { \left. { \left( { - \cos \theta }\right) }\right|_0^\pi }\right] } = \\ = { abc\int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } d\rho } \cdot \left( { - \cos \pi + \cos 0 }\right) } = { 2abc\int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } d\rho } } = { 2abc\int\limits_0^ { 2\pi } { d\varphi } \cdot \left[ { \left. { \left( { \frac { { { \rho ^5 } } } { 5 } }\right) }\right|_0^1 }\right] } = \\ = { \frac { { 2abc } } { 5 } \int\limits_0^ { 2\pi } { d\varphi } } = { \frac { { 2abc } } { 5 } \cdot \left[ { \left. \varphi \right|_0^ { 2\pi } }\right] } = { \frac { { 2abc } } { 5 } \cdot 2\pi = \frac { { 4abc\pi } } { 5 } . } $

Пример 14

Вычислить интеграл $\int\limits_0^1 { dx } \int\limits_0^ { \sqrt { 1 - { x^2 } } } { dy } \int\limits_0^ { \sqrt { 1 - { x^2 } - { y^2 } } } { { { \left( { { x^2 } + { y^2 } + { z^2 } }\right) } ^2 } dz } ,$ используя сферические координаты.

Решение:

Область интегрирования представляет собой часть шара, расположенная в первом октанте и, следовательно, ограничена неравенствами $ { 0 \le \rho \le 1, } \;\; { 0 \le \varphi \le \frac { \pi } { 2 } , } \;\; { 0 \le \theta \le \frac { \pi } { 2 } . } $

Учитывая, что подынтегральное выражение равно $ { { \left( { { x^2 } + { y^2 } + { z^2 } }\right)^2 } } = { { \left[ { { { \left( { \rho \cos \varphi \sin \theta }\right) } ^2 } + { { \left( { \rho \sin \varphi \sin \theta }\right) } ^2 } + { { \left( { \rho \cos \theta }\right) } ^2 } }\right]^2 } } = \\ = { { \left[ { { \rho ^2 } { { \cos } ^2 } \varphi \, { { \sin } ^2 } \theta + { \rho ^2 } { \sin^2 } \varphi \, { { \sin } ^2 } \theta + { \rho ^2 } { { \cos } ^2 } \theta }\right]^2 } } = { { \left[ { { \rho ^2 } { { \sin } ^2 } \theta \underbrace { \left( { { { \cos } ^2 } \varphi + { \sin^2 } \varphi }\right) } _1 + { \rho ^2 } { { \cos } ^2 } \theta }\right]^2 } } = { { \left[ { { \rho ^2 } { { \sin } ^2 } \theta + { \rho ^2 } { { \cos } ^2 } \theta }\right]^2 } } = \\ = { { \left[ { { \rho ^2 } \underbrace { \left( { { { \sin } ^2 } \theta + { { \cos } ^2 } \theta }\right) } _1 }\right]^2 } } = { { \rho ^4 } , } $

а дифференциалы связаны соотношениями $dxdydz = { \rho ^2 } \sin \theta d\rho d\varphi d\theta ,$ получаем $ { I = \int\limits_0^1 { dx } \int\limits_0^ { \sqrt { 1 - { x^2 } } } { dy } \int\limits_0^ { \sqrt { 1 - { x^2 } - { y^2 } } } { { { \left( { { x^2 } + { y^2 } + { z^2 } }\right) } ^2 } dz } } = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } \int\limits_0^1 { \left( { { \rho ^4 } \cdot { \rho ^2 } d\rho }\right) } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin \theta d\theta } } = \\ = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } \int\limits_0^1 { { \rho ^6 } d\rho } \cdot \left[ { \left. { \left( { - \cos \theta }\right) }\right|_0^ { \large\frac { \pi } { 2 } \normalsize } }\right] } = \\ = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } \int\limits_0^1 { { \rho ^6 } d\rho } \cdot \left( { - \cos \frac { \pi } { 2 } + \cos 0 }\right) } = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } \int\limits_0^1 { { \rho ^6 } d\rho } \cdot 1 } = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } \cdot \left[ { \left. { \left( { \frac { { { \rho ^7 } } } { 7 } }\right) }\right|_0^1 }\right] } = \\ = { \frac { 1 } { 7 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } } = { \frac { 1 } { 7 } \cdot \left[ { \left. \varphi \right|_0^ { \large\frac { \pi } { 2 } \normalsize } }\right] } = { \frac { 1 } { 7 } \cdot \frac { \pi } { 2 } } = { \frac { \pi } { { 14 } } . } $