Определение тройного интеграла. Теорема существования тройного интеграла

Пусть в пространстве $\mathbf { \textit { Oxyz } } $ задана ограниченная замкнутая область { объём } $\mathbf { \textit { V } } $, и пусть на области $\mathbf { \textit { V } } $ определена функция $\mathbf { \textit { f } } (\mathbf { \textit { x } } $, $\mathbf { \textit { y } } $, $\mathbf { \textit { z } } )$.

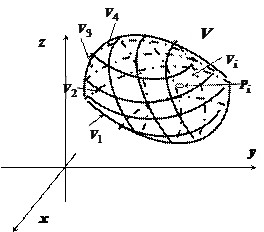
Разобьём область $\mathbf { \textit { V } } $ произвольным образом на $\mathbf { \textit { n } } $ подобластей $\mathbf { \textit { V } } _ { 1 } $, $\mathbf { \textit { V } } _ { 2 } $, $\mathbf { \textit { V } } _ { 3 } , { \ldots } , \mathbf { \textit { V } } _ { n } $, { не имеющих общих внутренних точек). Символом $\mathbf { \textit { v } } (\mathbf { \textit { V } } _ { i } )$ будем обозначать объём области $\mathbf { \textit { V } } _ { i } $; символом $\mathbf { \textit { d } } $ обозначим наибольший из диаметров областей $\mathbf { \textit { V } } _ { i } $: $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n } diam(V_i )$.

В каждой из подобластей $\mathbf { \textit { V } } _ { i } \mathbf { \textit { (i } } = 1,2, { \ldots } ,\mathbf { \textit { n } } )$ выберем произвольную точку $\mathbf { \textit { P } } _ { i } = (\mathbf { \textit { x } } _ { i } , \mathbf { \textit { y } } _ { i } , \mathbf { \textit { z } } _ { i } )$, вычислим в этой точке значение функции $\mathbf { \textit { f } } (\mathbf { \textit { P } } _ { i } ) = \mathbf { \textit { f } } (\mathbf { \textit { x } } _ { i } $, $\mathbf { \textit { y } } _ { i } $, $\mathbf { \textit { z } } _ { i } )$, и составим интегральную сумму $\sum\limits_ { i=1 } ^n { f(P_i )\cdot v(V_i ) } $.

Если существует предел последовательности интегральных сумм при $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n } diam(V_i )\to 0$, не зависящий ни от способа разбиения области $\mathbf { \textit { V } } $ на подобласти $\mathbf { \textit { V } } _ { i } $, ни от выбора точек $\mathbf { \textit { P } } _ { i } $, то функция $\mathbf { \textit { f } } (\mathbf { \textit { x } } , \mathbf { \textit { y } } , \mathbf { \textit { z } } )$ называется интегрируемой по области $\mathbf { \textit { V } } $, а значение этого предела называется тройным интегралом от функции $\mathbf { \textit { f } } (\mathbf { \textit { x } } , \mathbf { \textit { y } } , \mathbf { \textit { z } } )$по области $\mathbf { \textit { V } } $ и обозначается $\iiint\limits_V { f(P)dv } $.

Если расписать значение $\mathbf { \textit { f } } (\mathbf { \textit { P } } )$ через координаты точки $\mathbf { \textit { P } } $, и представить $\mathbf { \textit { dv } } $ как $\mathbf { \textit { dv = dx dy dz } } $, получим другое обозначение тройного интеграла: $\iiint\limits_V { f(x,y,z)dxdydz } $. Итак, кратко, $\iiint\limits_V { f(x,y,z)dxdydz } =\iiint\limits_V { f(P)dv } =\mathop { \lim } \limits_ { \begin{array} { l} d\to 0 \\ (n\to \infty ) \\ \end{array} } \sum\limits_ { i=1 } ^n { f(x_i ,y_i ,z_i )\cdot v(V_i ) } $.

Теорема существования тройного интеграла

Если подынтегральная функция $\mathbf { \textit { f } } (\mathbf { \textit { x } } $, $\mathbf { \textit { y } } $, $\mathbf { \textit { z } } )$ непрерывна на области $\mathbf { \textit { V } } $, то она интегрируема по этой области.