Механические приложения тройного интеграла

Пусть $\mathbf { \textit { V } } $ - тело в пространстве, в котором задано распределение объёмной плотности массы $\mu (P)(P\in V,\mu (P)=\mathop { \lim } \limits_ { diam(G)\to 0 } \frac { m(G) } { v(G) } $, где $\mathbf { \textit { G } } $ - область, содержащая точку $\mathbf { \textit { Р } } , \mathbf { \textit { m } } (\mathbf { \textit { G } } )$ - масса этой области, $\mathbf { \textit { v } } (\mathbf { \textit { G } } )$ - её объём } . Вывод следующих формул полностью аналогичен выводу для двумерного случая { раздел $\textbf { Механические приложения двойного интеграла } $ } , поэтому просто перечислим их.

Масса тела $m(v)=\iiint\limits_V { \mu (P)dv } $;

Объем тела (V = \large\iiint\limits_G\normalsize { dxdydz } );

Объем тела в цилиндрических координатах

(V = \large\iiint\limits_ { S\left( { r,\theta ,z }\right) } \normalsize { rdrd\theta dz } )

Объем тела в сферических координатах

(V = \large\iiint\limits_ { S\left( { r,\theta ,\varphi }\right) } \normalsize { { r^2 } \sin \theta drd\theta d\varphi } )

Плотность тела $\mu \left( { x,y,z }\right)$;

Координаты центра тяжести $x_c =\frac { 1 } { m(V) } \iiint\limits_V { x\cdot \mu (P)dv } $, $y_c =\frac { 1 } { m(V) } \iiint\limits_V { y\cdot \mu (P)dv } $, $z_c =\frac { 1 } { m(V) } \iiint\limits_V { z\cdot \mu (P)dv } $;

Моменты инерции

1. $I_ { Oxz } =\iiint\limits_V { y^2\cdot \mu (P)dv } $ { относительно плоскости $\mathbf { \textit { Oxz } } $ } ,
2. $I_ { Oyz } =\iiint\limits_V { x^2\cdot \mu (P)dv } $ { относительно плоскости $\mathbf { \textit { Oyz } } $ } ,
3. $I_ { Oxy } =\iiint\limits_V { z^2\cdot \mu (P)dv } $ { относительно плоскости $\mathbf { \textit { Oxy } } $ } ,
4. $I_x =\iiint\limits_V { (y^2+z^2)\cdot \mu (P)dv } $ { относительно оси $\mathbf { \textit { Ox } } $ } ,
5. $I_y =\iiint\limits_V { (x^2+z^2)\cdot \mu (P)dv } $ { относительно оси $\mathbf { \textit { Oy } } $ } ,
6. $I_z =\iiint\limits_V { (x^2+y^2)\cdot \mu (P)dv } $ { относительно оси $\mathbf { \textit { Oz } } $ } ,
7. $I_O =\iiint\limits_V { (x^2+y^2+z^2)\cdot \mu (P)dv } =I_ { Oxy } +I_ { Oyz } +I_ { Oxz } $ { относительно начала координат } .

Статические моменты тела относительно координатных плоскостей (x = 0), (y = 0) и (z = 0), с плотностью ( { \mu \left( { x,y,z }\right) } )

( { M_ { yz } } = \large\iiint\limits_G\normalsize { x\mu \left( { x,y,z }\right)dV } ), ( { M_ { xz } } = \large\iiint\limits_G\normalsize { y\mu \left( { x,y,z }\right)dV } ), ( { M_ { xy } } = \large\iiint\limits_G\normalsize { z\mu \left( { x,y,z }\right)dV } )

Пример 1

Найти координаты центра тяжести половины шара радиуса $\mathbf { \textit { R } } $, если плотность пропорциональна расстоянию от центра шара.

Решение:

Если ввести координатную систему так, как показано

на рисунке, то $\mu (P)=k\sqrt { x^2+y^2+z^2 } = kr$; вычисления ведём, естественно, в сферических координатах:

$m=\iiint\limits_V { kr\cdot r^2\sin \theta drd\varphi d\theta } =k\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { \pi /2 } { \sin \theta d\theta \int\limits_0^R { r^3dr } } = 2\pi k\cdot 1\cdot R^4/4=\pi kR^4/2 } $;

$x_c =\frac { 1 } { m } \iiint\limits_V { x\cdot kr\cdot r^2\sin \theta drd\varphi d\theta } =k\int\limits_0^ { 2\pi } { \cos \varphi d\varphi \int\limits_0^ { \pi /2 } { \sin ^2\theta d\theta \int\limits_0^R { r^4dr } } =0 } ,$

аналогично $\mathbf { \textit { y } } _ { c } $ = 0 { что, впрочем, очевидно и без вычислений } ;

$z_c =\frac { 1 } { m } \iiint\limits_V { z\cdot kr\cdot r^2\sin \theta drd\varphi d\theta } =\frac { 2k } { \pi kR^4 } \int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { \pi /2 } { \cos \theta \sin \theta d\theta \int\limits_0^R { r^4dr } } } =\frac { 2k } { \pi kR^4 } \cdot 2\pi \cdot \frac { 1 } { 2 } \cdot \frac { R^5 } { 5 } =\frac { 2R } { 5 } $.

Пример 2

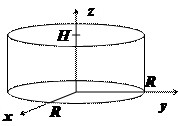
Найти моменты инерции однородного цилиндра относительно диаметра основания и оси.

Решение:

Если система координат введена так, как показано на рисунке, то мы должны найти $\mathbf { \textit { I } } _ { x } $ { или $\mathbf { \textit { I } } _ { y } =\mathbf { \textit { I } } _ { x } )$ и $\mathbf { \textit { I } } _ { z } $.

Вычисляем в цилиндрических координатах. $I_x =\iiint\limits_V { k(y^2+z^2)dxdydz } =k\int\limits_0^ { 2\pi } { \left( { \frac { R^4 } { 4 } H\sin ^2\varphi +\frac { H^3R^2 } { 6 } }\right)d\varphi } =\frac { \pi kHR^4 } { 4 } +\frac { \pi kH^3R^2 } { 3 } $

$ I_z =\iiint\limits_V { k(x^2+y^2)dxdydz } =\iiint\limits_V { kr^2\cdot rdrd\varphi dz } =k\cdot 2\pi \frac { R^4 } { 4 } \cdot H=\frac { \pi kHR^4 } { 2 } . $