Выборочная функция распределения

Мы рассматривали эмпирическую функцию распределения $F\ast ( x )=\frac { n_x } { n } $, определяющую относительную частоту события $X<x$

$F\ast ( x )=\left\{ { { \begin{array} { \c } { 0,x\leqslant x_1 } \\ { 1,x>x_1 } \\ \end{array} } }\right.$

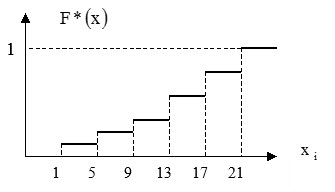
Построим выборочную функцию распределения в нашем примере { по центрам интервалов } . Наименьшее значение варианта $x_i =1$.

Следовательно $F\ast ( x )=0$, при $x\leqslant 1-$ это означает, что случайная величина X при $X<1$ наблюдалась ноль раз. Значение $X<5$ { а именно $X=1$ наблюдалось один раз } $F\ast ( x )=\frac { n_x } { n } =\frac { 1 } { 25 } , x\leqslant 5$

Значение $X<9$ { а именно $X=1$ и $X=5$, наблюдалось $1+6=7$ раз } , $F\ast ( x )=\frac { 7 } { 25 } , x\leqslant 9$

Значение $X<13$ { а именно $X=1$, $X=5$, $X=9$, наблюдалось $1+6+3=10$ раз } $F\ast ( x )=\frac { 10 } { 25 } , x\leqslant 13$

Значение $X<17$ { а именно $X=1$, $X=5$, $X=9$, $X=13$, наблюдалось $1+6+3+3=13$ раз } $F\ast ( x )=\frac { 13 } { 25 } , x\leqslant 17$

Значение $X<21$ { а именно $X=1$, $X=5$, $X=9$, $X=13$, $X=17$ наблюдалось $1+6+3+3+6=19$ раз } $F\ast ( x )=\frac { 19 } { 25 } , x\leqslant 21$

$F\ast ( x )=1$, при $x>21$

Выборочная функция имеет вид: $ x_i F\ast ( x ) F\ast ( x )=\left\{ { { \begin{array} { \c } { 0,x\leqslant 1 } \\ { \frac { 1 } { 28 } ,x\leqslant 5 } \\ { \frac { 7 } { 25 } ,x\leqslant 9 } \\ { \frac { 10 } { 25 } ,x\leqslant 13 } \\ { \frac { 13 } { 25 } ,x\leqslant 17 } \\ { \frac { 19 } { 25 } ,x\leqslant 21 } \\ { 1,x>21 } \\ \end{array} } }\right. $