Правило трех сигм

Преобразуем формулу $P( { \left| { X-a }\right|\prec \xi } )=2\Phi ( { \frac { \xi } { \sigma } } )$

Положим $\xi =t\cdot \sigma $получим $P( { \left| { X-a }\right|\prec \sigma \cdot t } )=2\Phi ( { \frac { t\cdot \sigma } { \sigma } } )$

Если $t=n,\,то\,\sigma t=n\sigma$, тогда $ P( {\left| { X-a }\right|\prec n\sigma } )=2\Phi ( n )=\left\{ { { \begin{array} { \c } { 0,6826\,,\,n=1 \Phi ( 1 )=0,3413 } \\ { 0,9545\,,\,n=2 \Phi ( 2 )=0,4772 } \\ { 0,9973\,,\,n=3 \Phi ( 3 )=0,4986 } \\ \end{array} } }\right. $

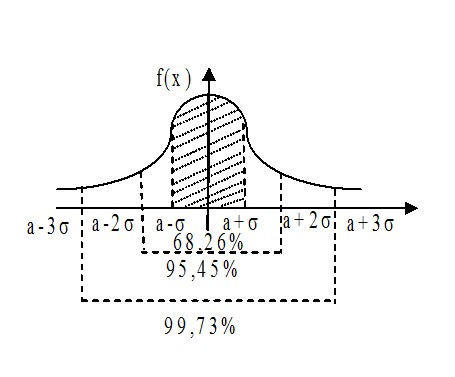
$\begin{array} { l } P( { \left| { X-a }\right|<\sigma } )=P( { a-\sigma <X<\sigma +a } )=0,6826 \\ P( { \left| { X-a }\right|<2\sigma } )=P( { a-2\sigma <X<2\sigma +a } )=0,9545 \\ P( { \left| { X-a }\right|<3\sigma } )=P( { a-3\sigma <X<3\sigma +a } )=0,9973 \\ \end{array} $

Суть правила

Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

Вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения равно 0,9973

На практике: если распределение случайной величины неизвестно, но условие, указанное в данном правиле выполняется, то есть основание предполагать, что случайная величина распределена нормально.