Понятие события, операции над событиями

Понятие события

Событие является первоначальным понятием в Т.В. Под событием понимается результат некоторого эксперимента. Т.В. интересуется только тем, произошло событие или нет.

События можно разделить на три класса.

1. Достоверное событие - всегда происходит в эксперименте - $\Omega $.
2. Невозможное событие - $\emptyset $- никогда не происходит.
3. Случайное событие - в одних и тех же условиях может происходить, а может не происходить, обозначается: $A=\left\{ { расшифровка }\right\} $

Например: эксперимент: подбрасываем монеты, результат эксперимента - случайное событие

$A=$ { монета упала гербом } ,

$B=$ { монета упала решкой } ,

$C=$ { монета упала ребром } .

В Т.В. событие и эксперимент не разделяют.

Опр Совокупность всех событий для данного эксперимента называется пространством элементарных событий. { Оно может быть конечным или бесконечным } .

Операции над событиями

Опр Произведением событий $A$ и $B$ называется событие С которое происходит тогда когда происходит и $A$ и $B$, обозначается: $C=A\cap B$.

Опр Произведением группы из n - событий - $A_1 \,,\,A_2 \ldots A_n $ есть событие $A$, обозначается $A=A_1 \cap A_2 \cap A_3 \ldots A_n $.

Опр Суммой событий $A$ и $B$ называется третье событие С которое происходит при наступлении хотя бы одного из событий $A$ или $B$, обозначается $C=A\cup B$.

Опр Суммой группы событий $A_1 \ldots A_n $ называется событие $C=A_1 \cup A_2 \cup \ldots \cup A_n $.

Опр Разностью событий $A$ и $B$ называется третье событие С которое происходит тогда когда $A$ происходит, а $B$ не происходит: $C=A / { \vphantom { A B } } B$.

Опр Событие $\overline A $ называется противоположным событию $A$, если оно происходит тогда, когда $A$ не происходит.

Опр Говорят, что событие $A$ влечет событие $B$, если при наступлении события $A$ обязательно происходит событие $B$, обозначается: $A\subset B$.

Опр События $A$ и $B$ называются равносильными или тождественными, если $A\subset B$ и $B\subset A$ т.е. при наступлении одного, второе обязательно происходит.

Опр События $A$ и $B$ называются несовместными, если они одновременно происходить не могут $A\cap B=\emptyset $.

Опр Группа событий называется полной, если хотя бы одно из событий происходит обязательно $A_1 \cup A_2 \cup A_3 \cup \ldots \cup A_n =\Omega $

Опр Полная группа событий называется полной группой попарно-несовместных событий, если любые два события этой группы одновременно произойти не могут.

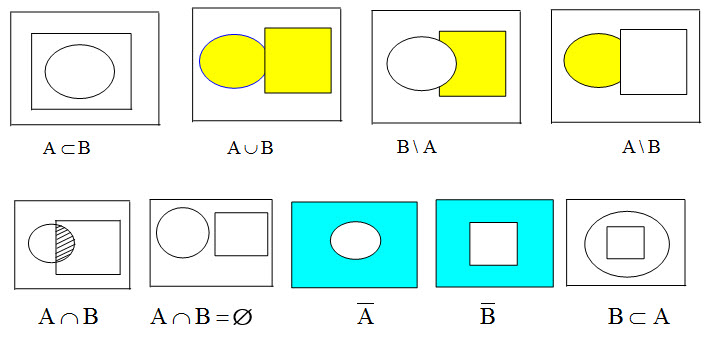
Геометрическая интерпретация операций над событиями

Пусть событие $A$ - { выбрали случайные точки, они попали в круг } , $B$ - { точки попали в квадрат }

Свойства операций над событиями

1. $A\cap A=A$
2. $A\cap \overline A =\emptyset $
3. $A\cap \Omega =A$
4. $A\cap \emptyset =\emptyset $
5. $A\cap B=B\cap A$
6. $A\cap ( { B\cap C } )=( { A\cap B } )\cap C$
7. $A\cup A=A$
8. $A\cup \overline A =\Omega $
9. $A\cup \Omega =\Omega $
10. $A\cup \emptyset =A$
11. $A\cup B=B\cup A$
12. $A\cup ( { B\cup C } )=( { A\cup B } )\cup C$
13. $A\cap ( { B\cup C } )=( { A\cap B } )\cup ( { A\cap C } )$
14. $A\cup ( { B\cap C } )=( { A\cup B } )\cap ( { A\cup C } )$

Формулы Де Моргана.

15. $\overline { A\cup B } =\overline A \cap \overline B $
16. $\overline { A\cap B } =\overline A \cup \overline B $