Показательное распределение

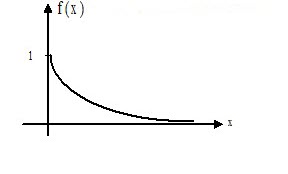
Показательным или экспоненциальным, называется распределение вероятностей непрерывной случайной величины $X$, которое описывается плотностью $ f( x )=\left\{ { { \begin{array} { \c } { 0, \,при\,x<0 } \\ { \lambda e^ { -\lambda x } ,при\,x\geqslant 0, \,\lambda -const } \\ \end{array} } }\right. $

и имеет один параметр $\lambda $. В этом его преимущество перед другими распределениями.

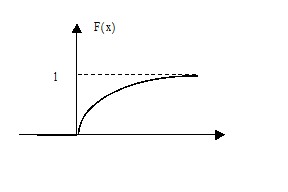
Найдем функцию распределения $F(x)$ $ \begin{array} { l } F( x )=\int\limits_ { -\infty } ^x { f( x )dx } =\int\limits_ { -\infty } ^0 { 0dx } +\int\limits_0^x { \lambda e^ { -\lambda x } dx } =\left. { \frac { \lambda e^ { -\lambda x } } { -\lambda } }\right|_0^x =-( { e^ { -\lambda x } -e^0 } )=1-e^ { -\lambda x } \\ F( x )=\left\{ { { \begin{array} { \c } { 0,\,x\leqslant 0 } \\ { 1-e^ { -\lambda x } ,\,x\geqslant 0 } \\ \end{array} } }\right. \\ \end{array} $

Найдём вероятность попадания в интервал { a,b } случайной величины, распределенной по показательному закону, заданному функцией распределения $ F( x )=\left\{ { { \begin{array} { \c } { 0,\,x\leqslant 0 } \\ { 1-e^ { -\lambda x } ,\,x\geqslant 0 } \\ \end{array} } }\right. $

используя формулу

$P( { a\leqslant x<b } )=F( b )-F( a )$ и учитывая, что $F( a )=1-e^ { -\lambda a } , F( b )=1-e^ { -\lambda b } $, получим $P( { a\leqslant x<b } )=1-e^ { -\lambda a } -1+e^ { -\lambda b } =e^ { -\lambda b } -e^ { -\lambda a } $

для $e^ { -x } -$ существуют таблицы.

Или $P( { a\leqslant x<b } )=e^ { -\lambda b } -e^ { -\lambda a } $

Числовые характеристики показательного распределения.

Пусть непрерывная, случайная величина $x$ распределена по показательному закону

$ f( x )=\left\{ { { \begin{array} { \c } { 0,\,при\,x<0 } \\ { \lambda e^ { -\lambda x } ,\,при\,x\geqslant 0 } \\ \end{array} } }\right. $

Найдём математическое ожидание

$M( x )=\int\limits_0^\infty { xf( x )dx } =\lambda \int\limits_0^\infty { xe^ { -\lambda x } dx } =$ $\left.| \begin{array} { \c } { u=x } \\ { dv=e^ { -\lambda x } dx } \\ \end{array} \begin{array} { \c } { du=dx } \\ { v=\frac { e^ { -\lambda x } } { -\lambda } } \\ \end{array} \right.| =\lambda ( -\left. { \frac { xe^ { -\lambda x } } { -\lambda } }\right|_0^\infty +\frac { 1 } { \lambda } \int\limits_0^\infty { e^ { -\lambda x } dx } )=$ $= \mathop { \lim } \limits_ { A\to \infty } \left. { \frac { x } { e^ { \lambda x } } } \right|_0^A -\mathop { \lim } \limits_ { A\to \infty } \left. { \frac { e^ { -\lambda x } } { \lambda } } \right|_0^A = \mathop { \lim } \limits_ { A\to \infty } ( { \frac { A } { e^ { \lambda A } } -\frac { 0 } { e^ { -0\lambda } } } )-\mathop { \lim } \limits_ { A\to \infty } \frac { 1 } { \lambda } ( { \frac { 1 } { e^ { \lambda A } } -\frac { 1 } { e^ { 0A } } } )=-\frac { 1 } { \lambda } \mathop { \lim } \limits_ { A\to \infty } ( { -\frac { 1 } { e^ { 0A } } } )=\frac { 1 } { \lambda } $

Дисперсия

$D( x )=\int\limits_0^\infty { x^2f( x )dx-M^2( x ) } =\lambda \int\limits_0^\infty { x^2e^ { -\lambda x } dx } = \left| по\,частям\,дважды \right| -M^2( x )= \frac { 2 } { \lambda ^2 } -\frac { 1 } { \lambda ^2 } =\frac { 1 } { \lambda ^2 } \\ \sigma ( x )=\sqrt { D( x ) } =\frac { 1 } { \lambda } $

Итак, параметры показательного распределения:

Математическое ожидание $M( x )=\frac { 1 } { \lambda } $.

Дисперсия $D(X)=\frac { 1 } { \lambda ^2 } $.

Среднее квадратическое отклонение $\sigma (X)=\frac { 1 } { \lambda } $