Нормальное распределение. Функция распределения

Нормальное распределение

Опр. Нормальным распределением называется распределение вероятностей, которое описывается плотностью. $ f( x )=\frac { 1 } { \sigma \sqrt { 2\pi } } \cdot e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } $ Видно, что нормальное распределение определяется двумя параметрами $a$ и $\sigma $.

Покажем, что $a$- математическое ожидание, $\sigma $- среднее квадратическое отклонение. $ \begin{array} { l } M( x )=\int\limits_ { -\infty } ^\infty { xf( x )dx=\frac { 1 } { \sigma \sqrt { 2\pi } } \cdot \int\limits_ { -\infty } ^\infty { \begin{array} { l } x\cdot e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } dx= \\ \\ \end{array} } \left| { { \begin{array} { \c } { z=\frac { x-a } { \sigma } } \\ { x=z\sigma +a } \\ { dx=\,\sigma \,dz } \\ \end{array} } }\right| } = \\ =\frac { 1 } { \sigma \sqrt { 2\pi } } \int\limits_ { -\infty } ^\infty { ( { z\sigma +a } )e^ { \frac { -z^2 } { 2 } } } \sigma dz=\frac { \sigma ^2 } { \sigma \sqrt { 2\pi } } \underbrace { \int\limits_ { -\infty } ^\infty { ze^ { \frac { -z^2 } { 2 } } dz } } _ { \begin{array} { l } Функция\,нечетная \\ интервал\,симметр. \\ интеграл=0 \\ \end{array} } + \\ +\frac { a\sigma } { \sigma \sqrt { 2\pi } } \underbrace { \int\limits_ { -\infty } ^\infty { e^ { \frac { -z^2 } { 2 } } } dz } _ { \begin{array} { l } Интеграл\,Пуассона \\ =\sqrt { 2\pi } \\ \end{array} } =a \\ \end{array} $

$ \begin{array} { l } D( x )=\frac { 1 } { \sigma \sqrt { 2\pi } } \int\limits_ { -\infty } ^\infty e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } dx=\left| { { \begin{array} { \c } { \frac { x-a } { \sigma } =z } \\ { x=z\sigma +a } \\ { dx=\sigma dz } \\ \end{array} } }\right|=\frac { 1 } { \sigma \sqrt { 2\pi } } \int\limits_ { -\infty } ^\infty { \sigma ^2z^2e^ { \frac { -z^2 } { 2 } } } \sigma dz= \\ \frac { \sigma ^2 } { \sqrt { 2\pi } } \int\limits_ { -\infty } ^\infty { z\cdot ze^ { \frac { -z^2 } { 2 } } } dz=\left| { { \begin{array} { \c } { u=z du=dz } \\ { dv=ze^ { \frac { -z^2 } { 2 } } dz v=-e^ { \frac { -z^2 } { 2 } } } \\ \\ \end{array} } }\right|= \frac { \sigma ^2 } { \sqrt { 2\pi } } ( { \underbrace { -ze^ { \frac { -z^2 } { 2 } } \left| { _ { -\infty } ^\infty }\right. } _0+\underbrace { \int\limits_ { -\infty } ^\infty { e^ { \frac { -z^2 } { 2 } } dz } } _ { \sqrt { 2\pi } } } )=\sigma ^2 \\ \sigma =\sqrt { D( x ) } =\sqrt { \sigma ^2 } =\sigma \\ \end{array} $

Нормальное распределение. Функция распределения

Нормальное распределение описывается плотностью распределения вероятностей $ f( x )=\frac { 1 } { \sigma \sqrt { 2\pi } } e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } . $ Из функции $f( x )$ видно, что нормальное распределение определяется двумя параметрами $a$ и $\sigma $.

Известно, что $a-$ математическое ожидание, а $\sigma-$ среднее квадратическое отклонение. Нормальное распределение с параметрами $a=0,\,\sigma =1$ называется нормированным или Гауссовым.

Его плотность $\varphi ( x )=\frac { 1 } { \sqrt { 2\pi } } e^ { \frac { -x^2 } { 2 } } $ Значения этой функции приведены в таблицах. Если $a$ и $\sigma- $произвольны, то распределение называется общим.

Функция распределения $F( x )$общего распределения, есть $ F( x )=\int\limits_ { -\infty } ^x { f( x )dx } =\frac { 1 } { \sigma \sqrt { 2\pi } } \int\limits_ { -\infty } ^x { e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } dx } $

Для нормированного распределения { Гауссово распределение } . $ F_0 ( x )=\int\limits_ { -\infty } ^x { f( x )dx } =\frac { 1 } { \sqrt { 2\pi } } \int\limits_ { -\infty } ^x { e^ { \frac { -x^2 } { 2 } } dx } $

Вероятность попадания нормированной нормальной величины X в интервал $( { 0,x } )$ можно найти, пользуясь функцией Лапласа. $ \Phi ( x )=\frac { 1 } { \sqrt { 2\pi } } \int\limits_0^x { e^ { \frac { -x^2 } { 2 } } } dx $

Действительно

$P( { 0<X<x } )=\int\limits_0^x { \varphi ( x )dx } =\frac { 1 } { \sqrt { 2\pi } } \int\limits_0^x { e^ { \frac { -x^2 } { 2 } } } dx=\Phi ( x )$, где $\varphi ( x )=\frac { 1 } { \sqrt { 2\pi } } \cdot e^ { - { x^2 } / 2 } $

Учитывая, что $\int\limits_ { -\infty } ^\infty { \varphi ( x )dx } =1$ и в силу симметрии $\varphi ( x )$ относительно нуля $\int\limits_ { -\infty } ^0 { \varphi ( x )dx=0,5 } $

Значит $P( { -\infty <x<0 } )=0,5$

Это легко получить:

$F( x )=\Phi ( x )+0,5-$ докажем, это: $ F( x )=P( { -\infty <X<x } )=P( { -\infty <x<0 } )+P( { 0<X<x } )=0,5+\Phi ( x ) $

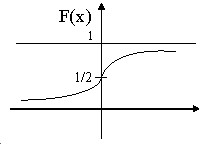
График функции распределения.

Для Гауссовой кривой, при $a=0$, $sigma =1$, $F_ ( x )=\frac { 1 } { \sqrt { 2\pi } } \int\limits_ { -\infty } ^x { e^ { \frac { -x^2 } { 2 } } dx } $

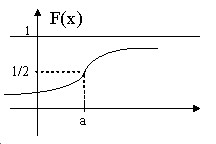
И для общего нормального распределения, при произвольных $a$ и $\sigma$

$F( x )=\int\limits_ { -\infty } ^x { f( x )dx } =\frac { 1 } { \sigma \sqrt { 2\pi } } \int\limits_ { -\infty } ^x { e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } dx } $