Нормальная кривая

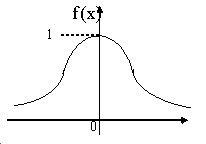
График плотности нормального распределения, называется нормальной кривой { кривой Гаусса } .

$f( x )=\frac { 1 } { \sigma \sqrt { 2\pi } } e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } $

Исследуем функцию и построим график

1). Функция определена на интервале $( { -\infty ,\infty } )$ $ \mathop { \lim } \limits_ { x\to -\infty } \frac { e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } } { \sigma \sqrt { 2\pi } } =0, \,\mathop { \lim } \limits_ { x\to +\infty } \frac { e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } } { \sigma \sqrt { 2\pi } } =0 $

2). Найдем точки, подозреваемые на экстремум $y'=\frac { 1 } { \sigma \sqrt { 2\pi } } e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } \cdot ( { -\frac { 2 } { 2\sigma ^2 } ( { x-a } ) } )=0$.

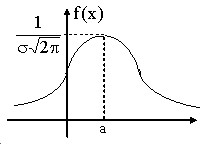
Здесь $x=a-$ критическая точка, $ y'( { x<a } )>0$, $y'( { x>a } )<0$, $x=a, y( a )=\frac { 1 } { \sigma \sqrt { 2\pi } } -$ максимум.

3). Найдем точки, подозреваемые на перегиб, для этого найдем вторую производную:

$y"=( { \frac { -( { x-a } ) } { \sigma ^3\sqrt { 2\pi } } e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } } )_x^ { ' } =-( { \frac { 1 } { \sigma ^3\sqrt { 2\pi } } e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } } )+\frac { ( { x-a } ) } { \sigma ^3\sqrt { 2\pi } } e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } \cdot ( { -( { \frac { 2( { x-a } ) } { 2\sigma ^2 } } ) } )=-\frac { 1 } { \sigma ^3\sqrt { 2\pi } } e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } ( { 1-\frac { ( { x-a } )^2 } { \sigma ^2 } } )=0$

получим $\sigma =\pm (x-a)$ или $x=a\pm \sigma -$ точки подозреваемые на перегиб. Представим производную в виде:

$y"=-\frac { 1 } { \sigma ^3\sqrt { 2\pi } } e^ { \frac { -( { x-a } )^2 } { 2\sigma ^2 } } ( { \frac { ( { \sigma -( { x-a } ) } )( { \sigma +( { x-a } ) } ) } { \sigma ^2 } } )=0 \Rightarrow x=\sigma +a, \Rightarrow x=a-\sigma $ точки подозреваемые на перегиб. Составим таблицу:

\begin{array} { |l|l|l|l|l|l|l|l| } \hline x & -\infty, a-\sigma & a-\sigma & a-\sigma, a & a & a,\sigma +a & \sigma +a & \sigma +a,+\infty \\ \hline y' & + & & + & 0 & - & & - \\ \hline y & \uparrow & & \uparrow & \frac\ { 1\ } \ { \sigma \sqrt \ { 2\pi \ } \ } \max & \downarrow & & \downarrow \\ \hline y'' & \succ 0 & 0 & \prec 0 & \frac\ { 1\ } \ { \sigma \sqrt \ { 2\pi \ } \ } \max & \prec 0 & 0 & \succ 0 \\ \hline y & вогнута & \frac\ { 1\ } \ { \sigma \sqrt \ { 2\pi \ } e\ } & выпукла & & выпукла & перегиб & вогнута \\ \hline \end{array}

Получим график функции плотности распределения вероятностей нормального распределения, который называется нормальной кривой.

Гауссово распределение