Непрерывная случайная величина

Непрерывная случайная величина. Функция распределения

Случайную величину $X$ будем называть непрерывной, если ее значения сплошь покрывают интервал $( a,b )$. Предполагается, что при каждом испытании случайная величина принимает только одно значение $x\in ( { a,b } )$. Мы уже говорили, что для характеристики случайной величины вводят функцию распределения.

Опр Функцией распределения называют функцию $F( x )$, определяющую вероятность того, что случайная величина $X$ в результате испытания примет значение меньше $x$. $F( x )=P( { X<x } )$

Дадим более полное определение случайной величины.

Опр. Случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Свойства функции распределения

1). Значения функции распределения принадлежат отрезку $\left[ { 0,1 }\right] 0\leqslant F( x )\leqslant 1$. Доказательство вытекает из смысла вероятности.

2). Функция распределения $F( x )-$ неубывающая функция т.е. $ F( { x_2 } )\geqslant F( { x_1 } )\,,\,если\,x_2 >x_1 $

Следствие 1 Вероятность того, что случайная величина примет значение заключенное в интервале $( a,b )$ равна приращению функции распределения на этом интервале. \begin{equation} \label { eq1 } P( { a\leqslant x<b } )=F( b )-F( a ) \qquad (1) \end{equation}

Следствие 2 Вероятность того, что непрерывная случайная величина примет одно определенное значение равна нулю.

3). Если возможные значения случайной величины принадлежат интервалу $( { a,b } )$, то

• $F( x )=0\,при\,x\leqslant a$
• $F( x )=1\,при\,x\geqslant b$

Следствие 3 Если возможные значения случайной величины расположены на всей оси $X$, то справедливы следующие предельные соотношения: $ \mathop { \lim } \limits_ { x\to -\infty } F( x )=0 , \mathop { \lim } \limits_ { x\to +\infty } F( x )=1 $

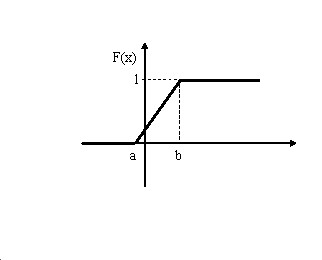
График функции распределения