F - распределение Фишера - Снедекора

Определение Пусть $U$ и $V -$ независимые случайные величины, распределённые по закону $\chi ^2( L )$ и $\chi ^2( k )$ с $L$ и $k-$ степенями свободы. Тогда распределение случайной величины

$ F( L,k )= { \frac { U } { L } } / { \frac { V } { k } } =\frac { { \chi ^2( L ) } / L } { { \chi ^2( k ) } / k } $

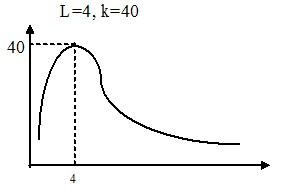f---raspredelenie-fishera---snedekora-0 называется $F-$ распределением с $L$ и $k-$ степенями свободы, т. к. $\chi ^2( L )\geqslant 0$и $\chi ^2( k )\geqslant 0$, то и $F( { L,k } )\geqslant 0$

Далее:

Условия независимости криволинейного интеграла от пути интегрирования

Вычисление криволинейного интеграла первого рода. Примеры

Специальные векторные поля

Вычисление двойного интеграла. Двукратный интеграл

Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных

Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы

Поток жидкости через поверхность

Вычисление поверхностного интеграла первого рода

Скалярное поле, производная по направлению, градиент

Булевы функции от $n$ переменных

Механические приложения тройного интеграла

Решение задач с помощью алгебры высказываний

Определение тройного интеграла. Теорема существования тройного интеграла

Логические следствия

Вычисление криволинейного интеграла первого рода. Плоский случай

Огравление $\Rightarrow $