Специальные векторные поля

Потенциальное векторное поле

Определение потенциального поля

Векторное поле $\bar { a } (\mathbf { \textit { M } } )$ называется потенциальным в области $\mathbf { \textit { V } } $, если существует такое скалярное поле $\varphi (M)$, что $\bar { a } (\mathbf { \textit { M } } )=grad\varphi (M)$ для $\forall M\in V$. Поле $\varphi (M)$ называется потенциалом поля $\bar { a } (\mathbf { \textit { M } } )$.

Свойства потенциального поля

1. Потенциал определён с точностью до произвольной постоянной $grad\varphi = grad(\varphi +C)$.
2. Разность потенциалов в двух точках $M_1 \in V,\,M_2 \in V$ определена однозначно.
3. Если поле $\bar { a } (\mathbf { \textit { M } } )$ потенциально, то линейный интеграл этого поля по любой кривой $\mathop { AB } \limits^\cup $, целиком лежащей в $\mathbf { \textit { V } } $, определяется только начальной и конечной точками этой кривой и не зависит от формы кривой. $W=\int\limits_ { \mathop { AB } \limits^\cup } { \bar { a } d\bar { r } } =\int\limits_ { \mathop { AB } \limits^\cup } { Pdx+Qdy+Rdz= } =\int\limits_ { \mathop { AB } \limits^\cup } { \frac { \partial \varphi } { \partial x } dx+\frac { \partial \varphi } { \partial y } dy+\frac { \partial \varphi } { \partial z } dz } =\int\limits_ { \mathop { AB } \limits^\cup } { d\varphi } =\left. { \varphi (P) }\right|_A^B =\varphi (B)-\varphi (A)$. Эта формула, как и в плоском случае, является обобщением формулы Ньютона-Лейбница для потенциального поля.
4. Циркуляция потенциального в области $\mathbf { \textit { V } } $ поля по любому контуру, лежащему в $\mathbf { \textit { V } } $, равна нулю.
5. Векторная линия потенциального поля в каждой точке $\mathbf { \textit { M } } $ ортогональна эквипотенциальной поверхности { т.е. поверхности уровня потенциала } , проходящей через точку $\mathbf { \textit { M } } $.
6. Ротор потенциального векторного поля равен нулю: $ rotgrad\varphi =\left| { \begin{array} { l } \,\,\bar { i } \,\,\,\bar { j } \,\,\bar { k } \\ \frac { \partial } { \partial x } \,\,\frac { \partial } { \partial y } \,\frac { \partial } { \partial z } \\ \frac { \partial \varphi } { \partial x } \,\frac { \partial \varphi } { \partial y } \,\frac { \partial \varphi } { \partial z } \\ \end{array} }\right|=\left( { \frac { \partial ^2\varphi } { \partial y\partial z } -\frac { \partial ^2\varphi } { \partial z\partial y } }\right)\bar { i } +\left( { \frac { \partial ^2\varphi } { \partial z\partial x } -\frac { \partial ^2\varphi } { \partial x\partial z } }\right)\bar { j } +\left( { \frac { \partial ^2\varphi } { \partial x\partial y } -\frac { \partial ^2\varphi } { \partial y\partial x } }\right)\bar { k } =0. $

Введём определение безвихревого поля: поле $\bar { a } (\mathbf { \textit { M } } )$, ротор которого в каждой точке равен нулю, называется безвихревым.

Мы доказали, что потенциальное поле необходимо безвихрево. Дальше мы займёмся достаточными условиями потенциальности.

Достаточные условия потенциальности

Теорема

Если область $\mathbf { \textit { V } } $ и поле $\bar { a } (\mathbf { \textit { M } } )$ удовлетворяют следующим условиям:

1. $\mathbf { \textit { V } } $ - односвязная область,
2. Поле $\bar { a } (\mathbf { \textit { M } } )$ - безвихрево { т.е. $rot\bar { a } (M)=\bar { 0 } $ } ,

то $\bar { a } (\mathbf { \textit { M } } )$ - потенциальное в $\mathbf { \textit { V } } $ поле.

Доказательство. Напомним определение односвязной области: область { на плоскости, в пространстве } называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области. Нам при доказательстве теоремы придётся строить поверхности, натянутые на контуры, определение односвязности как раз гарантирует, что такие поверхности существуют и ими могут служить поверхности, образующиеся при деформации контура в точку.

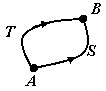
1. Докажем, что если выполняются условия теоремы, то линейный интеграл поля $\bar { a } (\mathbf { \textit { M } } )$ по любой кривой $\mathop { AB } \limits^\cup $, целиком лежащей в $\mathbf { \textit { V } } $, определяется только начальной и конечной точками этой кривой и не зависит от её формы. Пусть$\mathbf { \textit { ASB } } $ и $\mathbf { \textit { ATB } } $ - два пути, соединяющие точки $\mathbf { \textit { A } } $ и $\mathbf { \textit { B } } $. Вместе они образуют замкнутый контур $\mathbf { \textit { ASBTA } } $. Пусть $\sigma $ - кусочно-гладкая поверхность, натянутая на этот контур. Тогда по формуле Стокса $\oint\limits_ { ASBTA } { \bar { a } \cdot d\bar { r } } =\iint\limits_\sigma { rot\bar { a } \cdot \bar { n } d } \sigma =0$, так как $rot\bar { a } (M)=0$. Но $\oint\limits_ { ASBTA } { \bar { a } \cdot d\bar { r } } =\oint\limits_ { ASB } { \bar { a } \cdot d\bar { r } } +\oint\limits_ { BTA } { \bar { a } \cdot d\bar { r } } =\oint\limits_ { ASB } { \bar { a } \cdot d\bar { r } } -\oint\limits_ { ATB } { \bar { a } \cdot d\bar { r } } = 0\Rightarrow\oint\limits_ { ASB } { \bar { a } \cdot d\bar { r } } = \oint\limits_ { ATB } { \bar { a } \cdot d\bar { r } } $
2. Докажем, что если мы фиксируем точку $M_0 \in V$ и возьмём $\varphi (M)=\int\limits_ { \mathop { M_0 M } \limits^\cup } { \bar { a } d\bar { r } } $, то $\bar { a } (M)=grad\varphi (M)$, т.е. определённая таким образом функция $\varphi (M)$ действительно является потенциалом поля $\bar { a } (\mathbf { \textit { M } } )$.

Это доказательство полностью повторяет доказательство теоремы пункта Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути.

Именно, требуется доказать, что $\frac { \partial \varphi } { \partial x } =P(x,y,z),\,\frac { \partial \varphi } { \partial y } =Q(x,y,z),\,\frac { \partial \varphi } { \partial y } =R(x,y,z)$

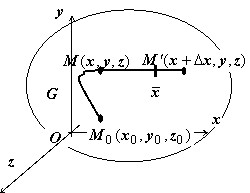
Действительно, пусть $M(x,y,z)\in G, { M } '(x+\Delta x,y,z)\in G.$ Тогда $\varphi (M)=\int\limits_ { \mathop { M_0 M } \limits^\cup } { Pdx+Qdy+Rdz } ,\varphi ( { M } ')=\int\limits_ { \mathop { M_0 M { M } ' } \limits^\cup } { Pdx+Qdy } +Rdz=\int\limits_ { \mathop { M_0 M } \limits^\cup } { Pdx+Qdy+Rdz } +\\+\int\limits_ { \mathop { M { M } ' } \limits^\cup } { Pdx+Qdy } +Rdz\Rightarrow \varphi (x+\Delta x,y,z)=\varphi (x,y,z)+\int\limits_x^ { x+\Delta x } { P(x,y,z)dx } \Rightarrow $

{ на $MM' y=const,z=const$ } $\Rightarrow \Delta _x \varphi (x,y,z)=\varphi (x+\Delta x,y,z)-\varphi (x,y,z)=\int\limits_x^ { x+\Delta x } { P(x,y,z)dx } = P(\bar x,y,z)\Delta x$ { по теореме о среднем }

$\Rightarrow \frac { \Delta _x \varphi } { \Delta x } =P(\bar { x } ,y,z)$. Точка $\bar { x } $ удовлетворяет условиям $x<\bar { x } <x+\Delta x$. Устремим $\Delta x\to 0$, тогда $\bar { x } \to x$ и $\mathop { \lim } \limits_ { \Delta x\to 0 } \frac { \Delta _x \varphi } { \Delta x } =\mathop { \lim } \limits_ { \bar { x } \to x } P(\bar { x } ,y,z)=P(x,y,z)$.

Аналогично доказывается, что $\frac { \partial \varphi } { \partial y } =Q(x,y,z),\,\frac { \partial \varphi } { \partial z } =R(x,y,z)$.