Скалярное поле, производная по направлению, градиент

Все физические процессы, проходящие в любой области пространства, характеризуются определёнными значениями некоторых величин. Так, нагревание тела описывается изменением температуры в точках этого тела; загнивание экономического региона характеризуется количеством остановленных в нём предприятий и т.д. Если каждой точке $\mathbf { \textit { M } } $ некоторой области $\mathbf { \textit { V } } $ пространства соответствует значение некоторой скалярной величины $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$, то говорят, что в области $\mathbf { \textit { V } } $ задано скалярное поле $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$. Поле называется стационарным, если оно не меняется во времени; мы будем изучать только стационарные поля.

Формально определение скалярного поля совпадает с определением функции $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$, заданной в области $\mathbf { \textit { V } } $; это верно и по существу, однако при изучении теории поля полезно иметь в виду, что функция $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$ описывает конкретную физическую реальность. Для изучения функциональной зависимости $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$ нам придётся ввести некоторую систему координат. Вид функции $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$ { её аналитическое выражение } меняется в зависимости от того, как введена координатная система { где расположено начало системы координат, куда направлены оси, каков масштаб измерения расстояний и т.д.), однако сущность, которую описывают эти разные выражения, одна и та же. Произвол в задании системы координат приводит к необходимости различать величины, не зависящие от конкретной системы (инвариантные относительно системы координат } , и величины, принимающие разные значения в разных системах { неинвариантные величины } .

Основной инвариантной величиной является, конечно, само значение $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$ поля в точке $\mathbf { \textit { M } } $. Мы будем называть поле $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$ гладким, если функция $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$ имеет непрерывные частные производные $\frac { \partial u } { \partial x } (M),\frac { \partial u } { \partial y } (M),\frac { \partial u } { \partial z } (M)$. Значения этих производных в точке $\mathbf { \textit { M } } $ зависят от системы координат, однако составленная с их помощью линейная комбинация базисных ортов системы $\frac { \partial u } { \partial x } \bar { i } +\frac { \partial u } { \partial y } \bar { j } +\frac { \partial u } { \partial z } \bar { k } $ образует градиент поля $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$ и инвариантна относительно системы координат.

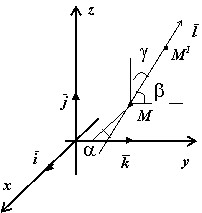
Вектор $grad\,u(M)$ направлен в сторону роста значений поля $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$ по направлению наибольшей скорости роста; длина $grad\,u(M)$ равна скорости роста в этом направлении. Инвариантна относительно системы координат производная поля в точке $\mathbf { \textit { M } } $ по любому направлению $\bar { l } $, выходящему из этой точки, так как она характеризует скорость изменения поля в направлении $\bar { l } $. Формально производная по направлению определяется как $\frac { \partial u } { \partial l } =\mathop { \lim } \limits_ { \begin{array} { l } M^1\to M \\ \mbox { вдоль } \bar { l } \\ \end{array} } \frac { u(M^1)-u(M) } { MM^1 } $, где $MM^1=\pm \vert \mathop { MM^1 } \limits^\to \vert $ в зависимости от того, имеют ли ось $\bar { l } $ и вектор $\mathop { MM^1 } \limits^\to $ одинаковые или противоположные направления.

Производная по направлению выражается через градиент формулой $ \frac { \partial u } { \partial l } (M)=gradu(M)\cdot \bar { l } _0 =\frac { \partial u } { \partial x } (M)\cos \alpha +\frac { \partial u } { \partial y } (M)\cos \beta +\frac { \partial u } { \partial z } (M)\cos \gamma =пр_l \left( { gradu(M) }\right), $ где $\bar { l } _0 \left\ { { \cos \alpha ,\cos \beta ,\cos \gamma }\right\ } $ - орт направления $\bar { l } $, $\cos \alpha ,\cos \beta ,\cos \gamma $ - направляющие косинусы этого направления.

В дальнейшем для обозначения градиента мы часто будем применять введённый Гамильтоном оператор $\nabla$ { "набла