Частные случаи векторных полей

Векторное поле называется однородным { или постоянным } , если $a(M)=\mathop { \mbox { const } } \limits^\to $.

Векторное поле называется плоским, если все векторы $\bar { a } (\mathbf { \textit { M } } )$ параллельны некоторой плоскости П и одинаковы вдоль каждого перпендикуляра к П. Если система координат введена так, что П совпадает с плоскостью $\mathbf { \textit { Оху } } $, то, очевидно, $\bar { a } (\mathbf { \textit { M } } )=P(x,y)\bar { i } +Q(x,y)\bar { j } $. Плоское поле достаточно рассматривать в пределах плоскости $\mathbf { \textit { Оху } } $, так как во всех плоскостях, параллельных $\mathbf { \textit { Оху } } $, оно одинаково.

Для плоского поля $diva=\frac { \partial P } { \partial x } +\frac { \partial Q } { \partial y } $, $rot\bar { a } =\left| { \begin{array} { l } \bar { i } \bar { j } \bar { k } \\ \frac { \partial } { \partial x } \frac { \partial } { \partial y } \frac { \partial } { \partial z } \\ PQO \\ \end{array} }\right|=\left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)\bar { k } $.

Пример плоского поля - магнитное поле, создаваемое током $\mathbf { \textit { I } } $, текущим по бесконечно длинному проводнику. Если ось $\mathbf { \textit { Oz } } $направлена вдоль этого проводника, то вектор напряженности магнитного поля равен $\bar { H } =2I\frac { -y\bar { i } +x\bar { j } } { x^2+y^2 } $, это поле определено везде, кроме оси $\mathbf { \textit { Oz } } $.

Векторное поле называется центральным, если в каждой точке $M\in V$ вектор $\bar { a } (\mathbf { \textit { M } } )$ коллинеарен радиусу-вектору этой точки: $\bar { a } (M)=u(M)\bar { r } (\bar { r } =x\bar { i } +y\bar { j } +z\bar { k } )$.

Так как $div\bar { r } =1+1+1=3, rot\bar { r } =\left| { \begin{array} { l } \bar { i } \bar { j } \bar { k } \\ \frac { \partial } { \partial x } \frac { \partial } { \partial y } \frac { \partial } { \partial z } \\ xyz \\ \end{array} }\right|=\bar { 0 } $, то для центрального поля $div\left( { u\cdot \bar { r } }\right)=\bar { r } \cdot gradu+udiv\bar { r } =3u+\bar { r } \cdot gradu$, $rot\left( { u\cdot \bar { r } }\right)=gradu\times \bar { r } +urot\bar { r } =gradu\times \bar { r } $.

Векторное поле называется центрально-симметричным, если оно центрально, и функция $\mathbf { \textit { u } } (\mathbf { \textit { M } } )$ зависит только от расстояния $\mathbf { \textit { r } } $, т.е. от длины радиуса-вектора точки $\mathbf { \textit { M } } : \bar { a } (M)=u(r)\bar { r } (r=\sqrt { x^2+y^2+z^2 } )$

Так как $gradr=\frac { x\bar { i } +y\bar { j } +z\bar { k } } { \sqrt { x^2+y^2+z^2 } } =\frac { \bar { r } } { r } , gradu(r)= { u } '(r)gradr= { u } '(r)\cdot \frac { \bar { r } } { r } $, то для центрально-симметричного поля $div\left( { u(r)\cdot \bar { r } }\right)=\bar { r } \cdot gradu(r)+u(r)div\bar { r } =3u+ { u } '(r)\cdot \bar { r } \cdot \frac { \bar { r } } { r } =3u+r { u } '(r), rot\left( { u(r)\cdot \bar { r } }\right)= \\ = gradu(r)\times \bar { r } +urot\bar { r } =\frac { { u } '(r) } { r } (\bar { r } \times \bar { r } )=\bar { 0 } $.

Найдем вид центрально-симметричного поля, для которого дивергенция равна нулю { в дальнейшем мы будем называть такие поля соленоидальными } : $3u+r { u } '(r)=0\Rightarrow \frac { du } { u } =-3\frac { dr } { r } \Rightarrow \ln \vert u\vert =-3\ln \vert r\vert +\ln \vert C\vert \Rightarrow u=\frac { C } { r^3 } \Rightarrow \bar { a } (M)=\frac { C } { r^3 } \bar { r } $.

Таким образом, соленоидальны только те центрально-симметричные поля, в которых зависимость от $\mathbf { \textit { r } } $ такая же, как в законах Кулона и всемирного тяготения. В связи с этим встают мировоззренческие вопросы о том, вычислял ли Господь Бог дивергенцию, когда создавал Вселенную, и о связи показателя степени в знаменателях законов Кулона и всемирного тяготения с пространственной размерностью мира, в котором мы живём

Векторные линии

Так как вектор $\bar { a } (\mathbf { \textit { M } } )$ определяется длиной и направлением в пространстве, задание в области $\mathbf { \textit { V } } $ поля $\bar { a } (\mathbf { \textit { M } } )$ равносильно заданию в $\mathbf { \textit { V } } $ полей длин и направлений. Геометрической характеристикой, определяющей в V поле направлений, служит совокупность векторных линий.

Векторной линией поля $\bar { a } (\mathbf { \textit { M } } )$ называется любая линия, которая в каждой своей точке $\mathbf { \textit { М } } $ касается вектора $\bar { a } (\mathbf { \textit { M } } )$.

В силовой интерпретации поля векторными линиями являются силовые линии поля, в гидродинамической - векторные линии есть траектории, по которым движутся частицы жидкости { линии тока } .

Получим дифференциальные уравнения векторных линий в декартовой системе координат.

Пусть векторная линия определяется векторным уравнением $\bar { r } =\bar { r } (t)=x(t)\bar { i } +y(t)\bar { j } +z(t)\bar { k } $. Тогда касательный вектор к этой линии $ { \bar { r } } '(t)=x(t { ) } '\bar { i } +y(t { ) } '\bar { j } +z(t { ) } '\bar { k } $ в любой точке должен быть коллинеарен полю, т.е. $x(t { ) } '\bar { i } +y(t { ) } '\bar { j } +z(t { ) } '\bar { k } =\lambda \left( { P\bar { i } +Q\bar { j } +R\bar { k } }\right)\Rightarrow \frac { dx } { dt } =\lambda P,\frac { dy } { dt } =\lambda Q,\frac { dz } { dt } =\lambda R\Rightarrow \\ \Rightarrow \frac { dx } { P(x,y,z) } =\frac { dy } { Q(x,y,z) } =\frac { dz } { R(x,y,z) } $

Эта записанная в симметричной форме система из трёх уравнений первого порядка и определяет векторные линии. Так как функции $\mathbf { \textit { P } } , \mathbf { \textit { Q } } , \mathbf { \textit { R } } $ одновременно не обращаются в нуль, то в любой точке одна из них отлична от нуля.

Пусть, например, в точке $М_0 \left( { x_0 ,y_0 ,z_0 }\right)\in V P\left( { x_0 ,y_0 ,z_0 }\right)\ne 0$. Тогда систему можно записать в виде $\frac { dy } { dx } =\frac { Q(x,y,z) } { P(x,y,z) } ;\frac { dz } { dx } =\frac { R(x,y,z) } { P(x,y,z) } $. Функции $\mathbf { \textit { P } } , \mathbf { \textit { Q } } , \mathbf { \textit { R } } $ непрерывно дифференцируемы, поэтому для последней системы выполняются условия теоремы существования и единственности задачи Коши с начальными условиями $y(x_0 )=y_0 ,z(x_0 )=z_0 $. Следовательно, через точку $\mathbf { \textit { M } } _ { 0 } $ проходит, и при том единственная, интегральная кривая системы, которая и будет векторной линией поля.

Пусть, например, поле $\bar { a } =x\bar { i } +y\bar { j } +2x^2\bar { k } $. Тогда векторные линии определяются системой $\frac { dx } { x } =\frac { dy } { y } =\frac { dz } { 2x^2 } $. Решая уравнение $\frac { dx } { x } =\frac { dy } { y } $, получим $\mathbf { \textit { y } } =\mathbf { \textit { C } } _ { 1 } \mathbf { \textit { x } } $, из уравнения $\frac { dx } { x } =\frac { dz } { 2x^2 } $ получаем $z=x^2+C_2 $, таким образом, уравнения векторных линий $\left\ { { \begin{array} { l } y=C_1 x, \\ z=x^2+C_2 . \\ \end{array} }\right.$

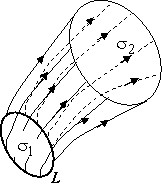
Пусть $\mathbf { \textit { L } } $ - некоторая кривая в области $\mathbf { \textit { V } } $, не являющаяся векторной линией. Проведём через каждую точку $\mathbf { \textit { L } } $ векторную линию; получившаяся в результате поверхность называется векторной поверхностью. Если $\mathbf { \textit { L } } $ - замкнутая линия, то поверхность называется векторной трубкой. Основное свойство векторной трубки: векторная линия, вошедшая в трубку через поперечное сечение $\sigma _1 $, может выйти из неё только через другое сечение $\sigma _2 $. Действительно, если бы векторная линия пересекла боковую поверхность векторной трубки, то через точку пересечения проходило бы две векторные линии, что, как мы установили, невозможно.