Расчет сварного соединения с угловыми швами на одновременное действие продольной и поперечной сил и момента

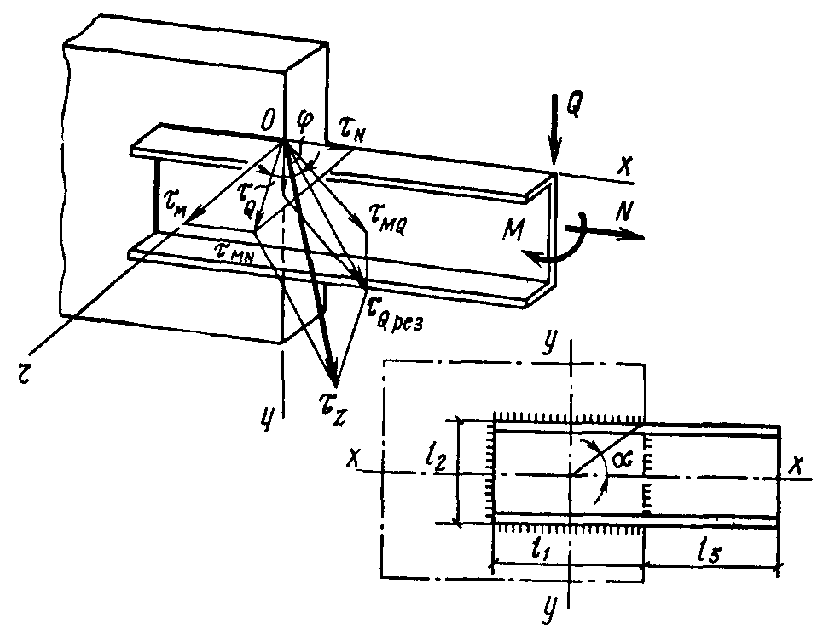
Консоль, подвергающаяся действию продольной и поперечной сил и момента, прикрепляется угловым швом по периметру соприкасающихся поверхностей { рис. 1 } .

Продольная сила $N = 195$ кН, поперечная сила $Q = 30$ кН, изгибающий момент $М = 24,5$ кНм. Материал консоли - сталь марки 18пс $R_ { un } = 370$ МПа, $R_ { wz } = 165$ МПа. Сварка выполняется полуавтоматом в углекислом газе проволокой диаметром 2 мм марки Св-08Г2С в нижнем положении $R_ { wf } = 215$ МПа; $\beta _ { f } = 0,9; \beta _ { z } = 1,05$. Коэффициенты условий работы $\gamma _ { wz } =\gamma _ { c } = 1$.

Рис. 1. К расчету сварного соединения с угловыми швами на одновременное действие продольной и поперечной сил и момента

Необходимо определить катет углового шва.

Решение

Сечение, по которому следует производить расчет сварного соединения для указанного сочетания стали, сварочной проволоки и способа сварки - по металлу границы сплавления. Принимаем $k_ { f } = 10$ мм.

1). Определяем напряжение в соединении от продольной силы $N:\tau _ { N } =N / A_ { w } $, где расчетная площадь шва $A_ { w } = 2 (l_ { 1 } +l_ { 2 } ) k_ { f } \beta _ { z } $.

С учетом того, что расчетная длина шва принимается меньше его полной длины на 10 мм $l_ { 1 } = 19,5$ см, $l_ { 2 } = 15,5$ см:

$A_ { w } = 2(19,5 + 15,5) \cdot 1 \cdot 1,05 = 73,5$ см$^ { 2 } $.

$\tau _ { N } = 195 \cdot 10 / 73,5 = 26,5$ МПа.

2). Определяем напряжение в соединении от поперечной силы $Q$.

Результирующее напряжение $\tau _ { Q рез } $ является суммой векторов напряжения от силы $Q$, перенесенной в центр тяжести периметра швов $(\tau _ { Q } )$ и напряжения от момента $(\tau _ { мQ } )$:

$\tau _ { Q } =Q / A_ { w } = 30 \cdot 10 / 73,5 = 4,1$ МПа; $ \tau _ { мQ } =M\sqrt { x^2+y^2 } /\left( { I_ { zx } +I_ { zy } }\right). $

Моменты инерции расчетного сечения соединения по металлу границы сплавления относительно его главных осей:

$I_ { zx } \approx \beta _ { z } { \ { } 2l^ { 3 } _ { 2 } k_ { f } / 12 + 2l_ { 1 } k_ { f } [(l_ { 2 } +k_ { f } ) / 2]^ { 2 } { \ } } = \\ = 1,05 { \ { } 2 \cdot 15,5^ { 3 } \cdot 1/12 + 2 \cdot 19,5 \cdot 1[(15,5 + 1) / 2]^ { 2 } { \ } } = 3439$ см$^ { 4 } $,

$I_ { zy } \approx \beta _ { z } { \ { } 2l^ { 3 } _ { 1 } k_ { f } / 12 + 2l_ { 2 } k_ { f } [(l_ { 1 } +k_ { f } ) / 2]^ { 2 } { \ } } = \\ = 1,05 { \ { } 2 \cdot 19,5^ { 3 } \cdot 1/12 + 2 \cdot 15,5 \cdot 1 [(19,5 + 1) / 2]^ { 2 } { \ } } = 4717$ см$^ { 4 } $.

Расстояние точки шва, наиболее удаленной от центра тяжести расчетного сечения соединения:

$\sqrt { x^2+y^2 } =\sqrt { 10^2+8^2 } =12,8$ см.

$\tau _ { мQ } = 30 \cdot 10^ { 3 } \cdot 12,8 / 8156 = 47$ МПа.

Результирующее напряжение от действия поперечной силы в плоскости $XOY$:

$\tau _ { Q { рез } } =\sqrt { \tau _Q^2 +\tau _ { мQ } ^2 +2\tau _Q \tau _ { мQ } \cos \alpha } $ ,

где $\alpha $ - угол, определяемый размерами соединения (см. рис. \href { } { 17 } ).

$\tau _ { Q { рез } } =\sqrt { 4,1^2 +47^2 +2\cdot 4,1\cdot 47\cdot 0,78 } =50,3$ МПа.

3). Определение напряжения в соединении от момента $М$:

$\tau _ { м } =Мy_ { max } / I_ { zy } $;

$y_ { max } =l_ { 1 } / 2 + k_ { f } = 20 / 2 + 1 = 11$ см;

$\tau _ { м } = 24,5 \cdot 10^ { 3 } \cdot 11 / 4717 = 57$ МПа.

4). Результирующее напряжение от действия продольной силы $N$ и момента $М $ в плоскости $XOZ$:

$\tau _ { мN } =\sqrt { \tau _м^2 +\tau _N^2 } =\sqrt { 57^2 +26,5^2 } =62,8$ МПа.

5). Определение угла между векторами $\vec { \tau } _ { мN } $ и $\vec { \tau } _ { Q { рез } } $.

Угол $\phi $ определяют, пользуясь координатным методом в пространстве и свойством скалярного произведения двух векторов: $ \cos \varphi =\vec { a } \vec { b } /\left( { \left| { \vec { a } }\right|\cdot \left| { \vec { b } }\right| }\right), $ где $\vec { a } $ и $\vec { b } $ - векторы; $\vert \vec { a } \vert $ и $\vert \vec { b } \vert $ - длины векторов.

Поскольку скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов $\vec { a } \cdot \vec { b } =x_ { 1 } x_ { 2 } +y_ { 1 } y_ { 2 } $ и длина вектора равна корню квадратному из суммы квадратов его координат $\left| { \vec { a } }\right|=\sqrt { x_1^2 +y_1^2 +z_1^2 } , \cos \varphi =\left( { x_1 x_2 +y_1 y_2 +z_1 z_2 }\right)/\left( { \sqrt { x_1^2 +y_1^2 +z_1^2 } \sqrt { x_2^2 +y_2^2 +z_2^2 } }\right)$.

В рассматриваемом примере координаты вектора $\vec { \tau } _ { мN } $:

$х_ { 1 } = \tau _ { N } ; y_ { 1 } = 0; z_ { 1 } =\tau _ { м } $;

координаты вектора $\vec { \tau } _ { Q { рез } } $:

$x_ { 2 } =\tau _ { мQ } sin \alpha ; y_ { 2 } =\tau _ { мQ } cos \alpha +\tau _ { Q } ; z_ { 2 } = 0$; $ \begin{array} { c } \cos \varphi =\tau _N \tau _ { мQ } \sin \alpha /\left[ { \tau _ { мQ } \sqrt { (\tau _ { мQ } \sin \alpha )^2+(\tau _ { мQ } \cos \alpha +\tau _Q )^2 } }\right]= \\ =26,5\cdot 47\cdot 0,625/\left[ { 62,8\sqrt { (47\cdot 0,625)^2+(47\cdot 0,78+4,1)^2 } }\right]=0,25. \\ \end{array} $

6). Определяем суммарное напряжение в соединении

$\tau _z =\sqrt { \tau _ { мN } ^2 +\tau _ { Q { рез } } ^2 +2\tau _ { мN } \tau _ { Q { рез } } \cos \varphi } =\sqrt { 62,8^2+50,3^2+2\cdot 62,8\cdot 50,3\cdot 0,25 } =89,7$ МПа,

$\tau _ { z } / R_ { wz } = 89,7 / 165 = 0,54$.

Таким образом, при $k_ { f } = 10$ мм суммарное напряжение в 0,54 раза меньше расчетного сопротивления. Следовательно, катет шва в соединении следует принять $k_ { f } $ = 6 мм.

7). Проверяем прочность соединения при $k_ { f } = 6$ мм:

Проверка прочности соединения при $k_ { f } = 5$ мм показывает правильность расчета:

$А_ { w } = 2 (19,5 + 15,5) 0,6 \cdot 1,05 = 44,1$ см$^ { 2 } $;

$\tau _ { N } = 195 \cdot 10 / 44,1 = 44,2$ МПа;

$\tau _ { Q } = 30 \cdot 10 / 44,1 = 6,8$ МПа;

$I_ { zx } = 1983 см^ { 4 } ; I_ { zy } = 2754$ см$^ { 4 } $;

$\tau _ { мQ } = 30 \cdot 10^ { 3 } \cdot 12,8 / 4737 = 81$ МПа;

$\tau _ { Q { рез } } =\sqrt { 6,8^2 +81^2 +2\cdot 6,8\cdot 81\cdot 0,78 } =86,4$ МПа;

$\tau _ { м } = 24,5 \cdot 10^ { 3 } \cdot 10,3 / 2754 = 92$ МПа;

$\tau _ { мN } =\sqrt { 92^2 +44,2^2 } =102$ МПа;

$\cos \varphi =44,2\cdot 81\cdot 0,625/\left[ { 102\sqrt { \left( { 81\cdot 0,625 }\right)^2+\left( { 81\cdot 0,78+6,8 }\right)^2 } }\right]=0,25$;

$\tau _z =\sqrt { 102^2+86,4^2+2\cdot 102\cdot 86,4\cdot 0,25 } =149 < 165$ МПа.