Расчет сварного соединения с угловыми швами на действие момента в плоскости расположения швов

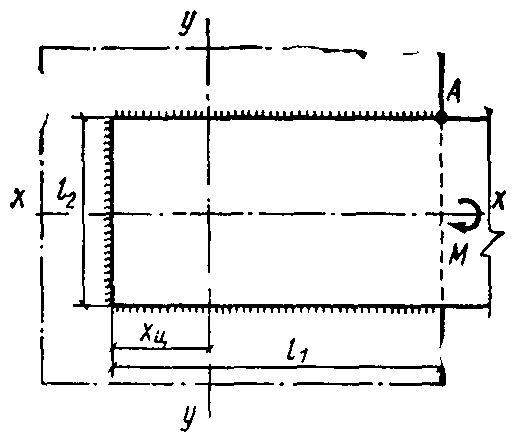
Полоса прикрепляется двумя горизонтальными и одним вертикальным швом { рис. 1 } .

Изгибающий момент $M = 55$ кНм. Материал пластины - сталь марки ВСт3 $R_ { un } = 370$ МПа. Сварка выполняется покрытыми электродами типа Э46 $R_ { wf } = 200$ МПа, $\beta _ { f } = 0,7$. Коэффициенты условий работы $\gamma _ { wf } =\gamma _ { c } = 1$. Необходимо определить катет углового шва.

Решение

Для указанного сочетания стали, электродов и способа сварки расчетным сечением является сечение по металлу шва, поэтому расчет должен выполняться по формуле: $ M/(I_ { fx } +I_ { fy } )\sqrt { x^2+y^2 } \leqslant R_ { wf } \gamma _ { wf } \gamma _c$

Рис. 1. К примеру расчета сварного соединения с угловыми швами на действие момента в плоскости расположения швов

Центр тяжести периметра швов определяется по формуле

$x_ { \mbox { ц } } = (l^ { 2 } _ { 1 } - 0,5 l_ { 2 } k_ { f } ) / (2l_ { 1 } +l_ { 2 } )$.

При $k_ { f } = 10$ мм $х_ { \mbox { ц } } = (900 - 0,5 \cdot 20) / (60 + 20) = 11$ см.

Координаты точки $A$, наиболее удаленной от центра тяжести расчетного сечения швов, $х = 19$ см, $у = 10$ см.

Моменты инерции расчетного сечения соединения по металлу шва относительно его главных осей:

$I_ { fx } \approx \beta_ { f } { \ { } l^ { 3 } _ { 2 } k_ { f } / l_ { 2 } + 2l_ { 1 } k_ { f } [(l_ { 2 } +k_ { f } ) / 2]^ { 2 } { \ } } $; $I_ { fy } \approx \beta _f \left[{ 2\left[ { \frac { l_1^3 k_f } { 12 } +l_1 k_f \left( { \frac { l_1 } { 2 } -x_ц }\right)^2 }\right]+l_2 k_f \left( { x_ц +\frac { k_f } { 2 } }\right)^2 }\right]$

Для углового шва $k_ { f } = 10$ мм с учетом того, что расчетная длина шва принимается меньше его полной длины на 10 мм $(l_ { 1 } = 29 см)$:

$I_ { fx } = 0,7 { \ { } 20^ { 3 } \cdot 1/12 + 2 \cdot 29 \cdot 1 [(20 + 1) / 2]^ { 2 } { \ } } = 4942 см^ { 4 } $;

$I_ { fy } = 0,7 { \ { } 2[29^ { 3 } \cdot 1/12 + 29 \cdot 1 (29 / 2 - 11)^ { 2 } ] + 20 \cdot 1 (11 + 1/2)^ { 2 } { \ } } = 5194 см^ { 4 } $;

Расстояние от центра тяжести периметра швов до точки $А$

$\sqrt { x^2+y^2 } =\sqrt { 11^2+10^2 } =21,5$ см.

Напряжения в соединении:

$\tau _ { f } = 55 \cdot 10^ { 3 } \cdot 21,5 / (4942 + 5194) = 117$ МПа.

$\tau _ { f } / R_ { wf } = 117 / 200 = 0,58$.

Таким образом, при $k_ { f } = 10$ мм напряжения в соединении $\tau _ { f } $ составляют 0,58 от расчетного сопротивления $(R_ { wf } )$. Следовательно, катет шва в соединении должен быть принят $k_ { f } = 5,8$ мм $\approx 6$ мм.

Проверка прочности соединения при $k_ { f } = 6$ мм показывает правильность расчета:

$I_ { fx } = 2864 см^ { 4 } ; I_ { fy } = 3078 см^ { 4 } ; \sqrt { x^2+y^2 } = 21,5$ см.

$\tau _ { f } = 55 \cdot 10^ { 3 } \cdot 21,5 / 5942 = 199 < 200$ МПа.