Вычисление поверхностного интеграла второго рода
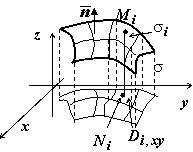
Пусть поверхность $\sigma $ взаимно однозначно проецируется в область $D_ { xy } $ на плоскости $\mathbf { \textit { Oxy } } $. В этом случае $\cos \gamma $ имеет одинаковый знак во всех точках поверхности. Именно, $\cos \gamma >0$, если рассматривается верхняя сторона поверхности, и $\cos \gamma <0$, если рассматривается нижняя сторона.
Поэтому для верхней стороны все слагаемые в интегральной сумме должны браться со знаком "+", и сумма будет иметь вид $\sum\limits_ { i=1 } ^n { R(M_i )\cdot s(D_ { i,xy } ) } =\sum\limits_ { i=1 } ^n { R(x_i ,y_i ,z_i )\cdot s(D_ { i,xy } ) } $.
Если поверхность задана уравнением $z=F(x,y)$, $(x,y)\in D_ { xy } $, то эта сумма равна $\sum\limits_ { i=1 } ^n { R(x_i ,y_i ,z(x_i ,y_i ))\cdot s(D_ { i,xy } ) } $. В последней сумме легко увидеть интегральную сумму для двойного интеграла $\iint\limits_ { D_ { xy } } { R(x,y,z(x,y))dxdy } $.
Переход к пределу при $\mathop { \max } \limits_ { i=1,2,\ldots n } diam\sigma _i \to 0$ { при этом и $\mathop { \max } \limits_ { i=1,2,\ldots n } diam D_ { i,xy } \to 0$ } даст
$\iint\limits_\sigma { R(x,y,z)dxdy } =\iint\limits_ { D_ { xy } } { R(x,y,z(x,y)) } dxdy$
Ясно, что эта формула получена для верхней стороны поверхности. Если выбрана нижняя сторона, то все слагаемые в интегральной сумме должны браться со знаком "-", и интегральная сумма будет иметь вид $-\sum\limits_ { i=1 } ^n { R(M_i )\cdot s(D_ { i,xy } ) } =-\sum\limits_ { i=1 } ^n { R(x_i ,y_i ,z_i )\cdot s(D_ { i,xy } ) } $.
Рассуждая, как и для верхней стороны, получим, что в этом случае $\iint\limits_\sigma { R(x,y,z)dxdy } =-\iint\limits_ { D_ { xy } } { R(x,y,z(x,y)) } dxdy$. Окончательно, $\iint\limits_\sigma { R(x,y,z)dxdy } =\pm \iint\limits_ { D_ { xy } } { R(x,y,z(x,y)) } dxdy$, где знак "+" берётся для верхней стороны поверхности, знак "-" - для нижней стороны.
Аналогично изложенному, для других интегралов: $\iint\limits_\sigma { P(x,y,z)dydz } =\pm \iint\limits_ { D_ { yz } } { P(x(y,z),y,z) } dydz$, если поверхность однозначно проецируется в область $D_ { yz } $ на плоскости $\mathbf { \textit { Oyz } } $, при этом знак "+" берётся для "передней" стороны поверхности { где $\cos \alpha >0)$, для "задней" стороны, где $\cos \alpha <0$, берётся знак "-"; $\iint\limits_\sigma { Q(x,y,z)dxdz } =\pm \iint\limits_ { D_ { xz } } { Q(x,y(x,z),z) } dxdz$, если поверхность однозначно проецируется в область $D_ { xz } $ на плоскость $\mathbf { \textit { Oхz } } $, знак "+" берётся для "правой" стороны поверхности { где $\cos \beta >0$ } , для "левой" стороны, где $\cos \beta <0$, берётся знак "-". Как и для поверхностного интеграла первого рода, если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
Пример 1
Вычислить $I=\iint\limits_\sigma { (x+z)dydz+(8y-x)dxdz+(2x^2-y)dxdy } $, $\sigma $ - часть поверхности цилиндра $\mathbf { \textit { y } } =\frac { x^2 } { 4 } $, заключенная между плоскостями $\mathbf { \textit { x } } $=0, $\mathbf { \textit { x } } $=8, $\mathbf { \textit { z } } $=0, $\mathbf { \textit { z } } $=3. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью $\mathbf { \textit { Ox } } $.
Решение
Определяем знаки направляющих косинусов нормали cos$\alpha >$0, cos$\beta <$0, cos$\gamma $=0. Поэтому
$I=\iint\limits_\sigma { (x+z)dydz+ } (8y-x)dxdz+(2x^2-y)dxdy=\iint\limits_ { D_ { yz } } { (x(y,z)+z)dydz-\iint\limits_ { D_ { xz } } { (8y(x,z)-x)dxdz } } ,$ где $\mathbf { \textit { D } } _ { yz } = { \ { } (\mathbf { \textit { y } } ,\mathbf { \textit { z } } ): 0\leqslant \mathbf { \textit { y } } \leqslant 16, 0 \leqslant \mathbf { \textit { z } } \leqslant 3 { \ } } , \mathbf { \textit { D } } _ { xz } = { \ { } (\mathbf { \textit { x } } ,\mathbf { \textit { z } } ): 0 \leqslant \mathbf { \textit { x } } \leqslant 8, 0 \leqslant \mathbf { \textit { z } } \leqslant 3 { \ } } $ - проекции $\sigma $ на плоскости $\mathbf { \textit { Oyz } } $ и $\mathbf { \textit { Oxz } } $ соответственно.
Проекция поверхности $\sigma $ на плоскость $\mathbf { \textit { Oxy } } $ вырождается в линию - параболу $\mathbf { \textit { y } } =\frac { x^2 } { 4 } $, cos$\gamma =0$, поэтому интеграл по $\mathbf { \textit { D } } _ { xy } \mathbf { } $ в данном случае отсутствует. Вычислим отдельно интегралы по $\mathbf { \textit { D } } _ { yz } $ и $\mathbf { \textit { D } } _ { xz , } $ выражая $\mathbf { \textit { x } } (\mathbf { \textit { y } } ,\mathbf { \textit { z } } )$ и $\mathbf { \textit { y } } (\mathbf { \textit { x } } ,\mathbf { \textit { z } } )$ из уравнения поверхности
$\sigma: \mathbf { \textit { x } } (\mathbf { \textit { y } } ,\mathbf { \textit { z } } )=2\sqrt y , \mathbf { \textit { y } } (\mathbf { \textit { x } } ,\mathbf { \textit { z } } )=\frac { x^2 } { 4 } $.
$\iint\limits_ { D_ { yz } } { \mbox { ( } x\mbox { ( } y\mbox { , } z\mbox { )+ } z\mbox { ) } dydz } = \iint\limits_ { D_ { yz } } { \mbox { (2 } \sqrt y \mbox { + } z\mbox { ) } dydz } = \int\limits_0^3 { dz } \int\limits_0^ { 16 } { (2\sqrt y +z) } \mathbf { \textit { dy } } $=328,$\iint\limits_ { D_ { xz } } { \mbox { (8 } y\mbox { ( } x\mbox { , } z\mbox { )- } x\mbox { ) } dxdz } =\iint\limits_ { D_ { xz } } { \mbox { (2 } x^\mbox { 2 } \mbox { - } x\mbox { ) } dxdz } =\int\limits_0^3 { dz\int\limits_0^8 { (2x^2-x) } } \mathbf { \textit { dx } } $=928.
Окончательно $\mathbf { \textit { I } } = 328 - 928 = - 600$.
Пример 2
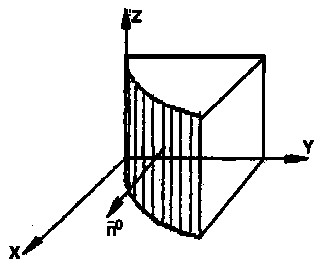
Вычислить $I=\iint\limits_\sigma { 3xdydz+zdxdz+5ydxdy } $, где $\sigma $ - часть плоскости $2x+3y-4z=12$, ограниченная координатными плоскостями $\mathbf { \textit { x } } =0, \mathbf { \textit { y } } =0, \mathbf { \textit { z } } =0$. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью $\mathbf { \textit { Oz } } $.
Решение
Из двух направлений нормали к $\sigma \bar { n } =\pm \frac { 2\bar { i } +3\bar { j } -4\bar { k } } { \sqrt { 4+9+16 } } $ мы должны выбрать такое, для которого коэффициент при орте $\bar { k } $ { т.е. $\cos \gamma )$ положителен, поэтому выбираем знак "-", тогда $\bar { n } =\frac { -2\bar { i } -3\bar { j } +4\bar { k } } { \sqrt { 29 } } $. В соответствии со знаками направляющих косинусов, $I=\iint\limits_\sigma { 3xdydz+zdxdz+5ydxdy } =-\iint\limits_ { D_ { yz } } { 3x(y,z)dydz } -\iint\limits_ { D_ { xz } } { zdxdz } + \iint\limits_ { D_ { xy } } { 5ydxdy } $. Вычисляем эти интегралы.
- $-3\iint\limits_ { D_ { yz } } { x(y,z)dydz } =\vert x=6-3y/2+2z\vert =-3\iint\limits_ { D_ { yz } } { \left( { 6-\frac { 3y } { 2 } +2z }\right)dydz } = =-3\int\limits_0^4 { dy\int\limits_ { \frac { 3 } { 4 } y-3 } ^0 { \left( { 6-\frac { 3 } { 2 } y+2z }\right)dz } } = \\ = -3\int\limits_0^4 { \left( { \frac { 9 } { 16 } y^2-\frac { 9 } { 2 } y+9 }\right)dy } =-3(12-36+36)=-36.$
- $-\iint\limits_ { D_ { xz } } { zdxdz } =-\int\limits_ { -3 } ^0 { zdz\int\limits_0^ { 6+2z } { dx } } =-\int\limits_ { -3 } ^0 { (6+2z)zdz } =27-18=9.$
- $5\iint\limits_ { D_ { xy } } { ydxdy } =5\int\limits_0^4 { ydy\int\limits_0^ { 6-\frac { 3 } { 2 } y } { dx } } =5\int\limits_0^4 { \left( { 6-\frac { 3 } { 2 } y }\right)ydy } = 5(48-32) = 80$
Окончательно, $I=-36+9+80=53.$
В заключение, вычисление поверхностного интеграла второго рода всегда можно свести к вычислению поверхностного интеграла первого рода. Так, в последнем примере подынтегральное выражение равно
$\left( { \bar { v } (M)\cdot \bar { n } (M) }\right)d\sigma $, где $\bar { v } (M)=3x\bar { i } +z\bar { j } +5y\bar { k } $, $\bar { n } (M)=\cos \alpha \bar { i } +\cos \beta \bar { j } +\cos \gamma \bar { k } =\frac { -2\bar { i } -3\bar { j } +4\bar { k } } { \sqrt { 29 } } $. Поэтому $\bar { v } (M)\cdot \bar { n } (M)=\frac { -6x-3z+20y } { \sqrt { 29 } } $, и, проектируя $\sigma $ на плоскость $\mathbf { \textit { Oxy } } \left( { d\sigma =\frac { dxdy } { \vert \cos \gamma \vert } =\frac { \sqrt { 29 } } { 4 } dxdy }\right)$, получим $I=\iint\limits_\sigma { 3xdydz+zdxdz+5ydxdy } =\iint\limits_\sigma { \frac { -6x-3z+20y } { \sqrt { 29 } } d\sigma = } \iint\limits_ { D_ { xy } } { \left. { \frac { -6x-3z+20y } { \sqrt { 29 } } \cdot \frac { \sqrt { 29 } } { 4 } }\right|_ { z=\frac { 1 } { 2 } x+\frac { 3 } { 4 } y-3 } dxdy= } \\ =\frac { 1 } { 4 } \iint\limits_ { D_ { xy } } { \left( { -\frac { 15 } { 2 } x+\frac { 71 } { 4 } y+9 }\right)dxdy=\frac { 1 } { 4 } \int\limits_0^6 { dx\int\limits_0^ { 4-\frac { 2 } { 3 } x } { \left( { -\frac { 15 } { 2 } x+\frac { 71 } { 4 } y+9 }\right)dy } } =\frac { 1 } { 4 } \int\limits_0^6 { \left( { \frac { 161 } { 18 } x^2-\frac { 250 } { 3 } x+178 }\right)dx= } } \\=\frac { 1 } { 4 } \left( { 644-1500+1068 }\right)=\frac { 212 } { 4 } =53$
Далее:
Определение криволинейного интеграла второго рода
Поток жидкости через поверхность
Вычисление криволинейного интеграла первого рода. Примеры
Теорема о предполных классах
Свойства тройного интеграла
Вычисление поверхностного интеграла второго рода
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Механические приложения тройного интеграла
Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы
Логические следствия
Теорема об аналоге СДНФ в Pk
Свойства криволинейного интеграла второго рода
Класс $T_1$. Теорема о замкнутости класса $T_1$
Булевы функции от $n$ переменных
Свойства потока векторного поля
Огравление $\Rightarrow $
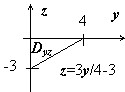
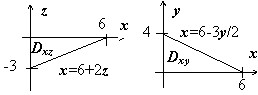
Комментарии ()