Поверхностный интеграл второго рода { по координатам } и его свойства

Поверхность $\sigma $ называется ориентируемой, если в каждой ее точке существует вектор нормали к $\sigma $, непрерывная вектор - функция на $\sigma $.

Поверхность $\sigma $ называется односторонней, если при обходе поверхности $\sigma $по контуру $\gamma $ вектор нормали меняет свое направление на противоположное.

Поверхность $\sigma $называется двусторонней, если при обходе поверхности $\sigma $по контуру $\gamma $ вектор нормали не меняет свое направление.

Примером односторонней поверхности является петля Мебиуса, примерами двусторонних поверхностей - плоскость, сфера, гиперболоиды и т.д.

Определение поверхностного интеграла второго рода

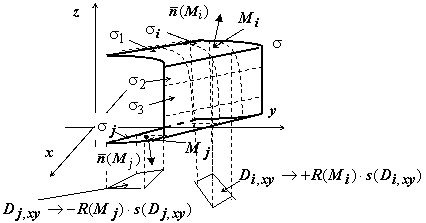
Пусть в пространстве переменных $\mathbf { \textit { x,y,z } } \mathbf { } $ задана ограниченная кусочно-гладкая двусторонняя поверхность $\sigma $, на которой введена ориентация { т.е. с помощью единичного вектора нормали в какой-либо точке $\sigma $ задана сторона поверхности } , и на которой определена функция $\mathbf { \textit { R } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } ,\mathbf { \textit { z } } )$

Разобьём поверхность на $n$ частей $\sigma _1 ,\sigma _2 ,\ldots \sigma _i ,\ldots \sigma _n $, на каждой из частей $\sigma _i $ выберем произвольную точку $M_i (x_i ,y_i ,z_i )$, найдём $R(M_i )=R(x_i ,y_i ,z_i )$, нормаль $\bar { n } (M_i )$ в точке $M_i $ к выбранной стороне поверхности, и площадь $s(D_ { i,xy } )$ проекции части $\sigma _i $ на плоскость $\mathbf { \textit { OXY } } $.

В интегральную сумму слагаемое $R(M_i )\cdot s(D_ { i,xy } )$ возьмём со знаком "+", если $\cos \gamma \geqslant 0$ { т.е. если угол $\gamma $ между $\bar { n } (M_i )$ и осью $\mathbf { \textit { Oz } } $ - острый; проекция $\bar { n } (M)$ на орт $\bar { k } $ оси $\mathbf { \textit { Oz } } $ положительна } , и со знаком "-", если $\cos \gamma <0$. В результате интегральная сумма будет иметь вид $\sum_ { i=1 } ^ { n } \pm R(M_ { i } )\cdot s(D_ { i,xy } )$

Если существует предел последовательности интегральных сумм при $\mathop { \max } \limits_ { i=1,2,\ldots n } diam\sigma _i \to 0$, не зависящий ни от способа разбиения поверхности $\sigma $ на части $\sigma _i (i=1,2,\ldots ,n)$, ни от выбора точек $M_i $, то функция $\mathbf { \textit { R } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } ,\mathbf { \textit { z } } )$ называется интегрируемой по поверхности $\sigma $, а значение этого предела называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам $\mathbf { \textit { x } } ,\mathbf { \textit { y } } $ и обозначается $\iint\limits_\sigma { R(M)\cdot dxdy } $.

Теорема существования

Если функция $\mathbf { \textit { R } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } ,\mathbf { \textit { z } } )$ непрерывна на поверхности $\sigma $, то она интегрируема по этой поверхности.

Если на поверхности $\sigma $, вместе с функцией $\mathbf { \textit { R } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } ,\mathbf { \textit { z } } )$, определены функции $\mathbf { \textit { P } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } ,\mathbf { \textit { z } } )$ и$\mathbf { \textit { Q } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } ,\mathbf { \textit { z } } )$, то, так же, как и интеграл $\iint\limits_\sigma { R(M)\cdot dxdy } $, определяются интегралы $\iint\limits_\sigma { P(M)\cdot dydz } $ и $\iint\limits_\sigma { Q(M)\cdot dxdz } $; в приложениях, как мы видели из рассмотренной в начале раздела физической задачи, обычно рассматривается сумма этих интегралов, которая обозначается $\iint\limits_\sigma { P(M)\cdot dydz+Q(M)\cdot dxdz+R(M)\cdot dxdy } $.

Запись поверхностного интеграла второго рода

Запишем вектор перемещений частиц и нормаль в точке $M(x, y, z)$, выделяя скалярные компоненты векторов

$\vec { a } \left( M \right)=P(x,\,y,\,z)\vec { i } +Q(x,\,y,\,z)\vec { j } +R(x,\,y,\,z)\vec { k } $,

$\vec { n } \left( M \right)=\cos \alpha \,\vec { i } +\cos \beta \vec { j } +\cos \gamma \vec { k } $

$\vec { a } \left( M \right)\cdot \vec { n } \left( M \right)=P\cos \alpha +Q\cos \beta +R\cos \gamma$

$ \iint\limits_\sigma { \vec { a } \cdot \vec { n } d\sigma } = \iint\limits_\sigma { (P\cos \alpha +Q\cos \beta +R\cos \gamma )d\sigma =\pm \iint\limits_\sigma { Pdydz } \pm \iint\limits_\sigma { Qdxdz } \pm \iint\limits_\sigma { Rdxdy } } $

$d\sigma \cos \alpha =\pm dydz, d\sigma \cos \beta =\pm dxdz, d\sigma \cos \gamma =\pm dxdy.$

Знак "+" выбирается, если угол между нормалью к поверхности и осью $OX$ в первом интеграле, $OY$ во втором, $OZ$ в третьем острый, знак "-" выбирается, если угол тупой. В самом деле, в поверхностных интегралах площади элементов поверхности положительны, а знаки "+" или "-" компенсируют знак косинуса угла между нормалью и координатной осью. При переходе от поверхностных интегралов к двойным одна из координат подставляется из уравнения поверхности, чтобы точка $(x, y, z)$ находилась на поверхности $\sigma $.

Свойства поверхностного интеграла второго рода

Для этого интеграла, как и для криволинейного интеграла второго рода, имеет смысл формулировать следующие свойства: линейность, аддитивность и зависимость поверхностного интеграла от выбора стороны поверхности: при изменении ориентации поверхности интеграл меняет знак

Т.е. любой поверхностный интеграл второго рода меняет знак при перемене стороны поверхности, постоянный множитель можно выносить за знак интеграла, поверхностный интеграл от суммы двух и более функций равен сумме поверхностных интегралов от этих функций, если поверхность разбита на конечное число частичных поверхностей, интеграл по всей поверхности равен сумме интегралов по частичным поверхностям.

Если $S$ - цилиндрическая поверхность с образующими, параллельными оси $OZ$, то $\iint\limits_S { R(x,y,z)dxdy } =0$. В случае, если образующие поверхности параллельны осям $OX$ и $OY$, то равны нулю соответствующие составляющие поверхностного интеграла второго рода.

Пример 1

Найти поток радиуса-вектора через полную поверхность тетраэдра, ограниченного координатными плоскостями и плоскостью $x + y + z = 1$

Поток радиус-вектора через координатные плоскости нулевой, так как на них радиус-вектор точки лежит в координатной плоскости и ортогонален нормали к координатной плоскости, т.е. $\vec { a } \cdot \vec { n } =0$.

Вычислим поток через грань тетраэдра, лежащую в плоскости $x + y + z =1$. Он и будет суммарным потоком, так как поток через остальные грани нулевой. Для этой грани $\vec { n } =\left\ { { \frac { 1 } { \sqrt 3 } ,\frac { 1 } { \sqrt 3 } ,\frac { 1 } { \sqrt 3 } }\right\ } ,\vec { a } =\vec { r } =\left\ { { x,y,z }\right\ } $, площадь грани - треугольника по теореме Пифагора равна $\frac { \sqrt 3 } { 2 } $

Поток равен $\prod=\iint\limits_\Delta { \vec { a } \cdot \vec { n } d\sigma =\iint\limits_\Delta { \frac { 1 } { \sqrt 3 } } } \left( { x+y+z }\right)d\sigma =\frac { 1 } { \sqrt 3 } \iint\limits_\Delta { d\sigma =\frac { 1 } { \sqrt 3 } } \frac { \sqrt 3 } { 2 } =\frac { 1 } { 2 } $

Поток равен $\prod=\iint\limits_\Delta { \vec { a } \cdot \vec { n } d\sigma } =\frac { 1 } { \sqrt 3 } \frac { \sqrt 3 } { 2 } =\frac { 1 } { 2 } $.

Вычислим поток через двойные интегралы проектированием на координатные плоскости. Поток радиус-вектора через координатные плоскости нулевой. Тогда $ \prod=\iint\limits_\Delta { \vec { a } \cdot \vec { n } d\sigma } =\iint\limits_ { D_ { yz } } { xdydz } +\iint\limits_ { D_ { xz } } { ydxdz } +\iint\limits_ { D_ { xy } } zdxdy=3\iint\limits_ { D_ { xy } } { zdxdy } =3\iint\limits_ { D_ { xy } } { z\left( { x,\,y }\right)dxdy } =\\=3\int\limits_0^1 { (\int\limits_0^ { 1-x } { (1-x-y)dy)dx=3\int\limits_0^1 { ((1-x)^2-\frac { 1 } { 2 } (1-x)^2)dx=\frac { 3 } { 2 } \int\limits_0^1 { \left( { x-1 }\right)^2dx } =\frac { 1 } { 2. } } } } $.

Получили тот же результат.