Поток жидкости через поверхность

Как и при изучении криволинейных интегралов, начнём с физической задачи. Пусть через объём $\mathbf { \textit { V } } $ течёт поток жидкости, имеющий скорость $\bar { v } (M)$ в точке $\mathbf { \textit { M } } $. Пусть в $\mathbf { \textit { V } } $ размещена проницаемая { возможно, воображаемая } поверхность $\sigma $. Требуется найти количество $\Pi $ жидкости, протекающей через $\sigma $ за единицу времени. В дальнейшем мы будем называть это количество потоком через поверхность.

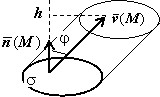
В случае, когда $\sigma $ - ограниченная плоская область и $\bar { v } (M)= \overline { const } $, решение очевидно. Это количество равно объёму, ограниченному цилиндрической поверхностью с основанием $\sigma $ и боковой стороной $\bar { v } (M)$. Площадь основания объёма равна $\sigma $ { этим символом мы обозначаем и поверхность, и её площадь } , высота $h=\mbox { пр } _ { \bar { n } } \bar { v } =\vert \bar { v } \vert \cos \varphi =\bar { v } \cdot \bar { n } $, т.е. равна скалярному произведению вектора скорости на единичный вектор нормали. Итак, $\Pi =\bar { v } \bar { n } \sigma $. Заметим, что изобразив на рисунке единичный вектор нормали, мы ввели на поверхности ориентацию. Так, применительно к рисунку справа, мы выбрали верхнюю сторону поверхности; если бы выбрали противоположную нормаль, поток изменил бы знак.

Возможны два способа представления этой величины.

1. Обозначив $f=(\bar { v } \cdot \bar { n } )$, получим $\prod = f\cdot\sigma$
2. Если в некоторой координатной системе $\bar { v } (M)$ имеет координаты $\mathbf { \textit { P } } $, $\mathbf { \textit { Q } } $, $\mathbf { \textit { R } } $, единичный вектор $\bar { n } (M)$ имеет координаты - направляющие косинусы $\cos \alpha ,\cos \beta ,\cos \gamma $, то $\Pi =\bar { v } \bar { n } \sigma =(P\cos \alpha +Q\cos \beta +R\cos \gamma )\sigma =P(\cos \alpha \cdot \sigma )+Q(\cos \beta \cdot \sigma )+R(\cos \gamma \cdot \sigma )$.

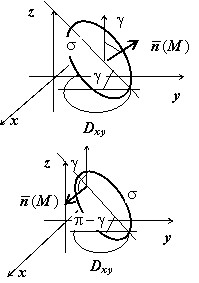
Чему равно произведение $\cos \gamma \cdot \sigma $? Произведение $\vert \cos \gamma \vert \cdot \sigma $ равно площади $s(D_ { xy } )$ проекции $D_ { xy } $ поверхности $\sigma $ на плоскость $\mathbf { \textit { Oxy } } $ { площади всегда положительны } .

Следовательно, $\cos \gamma \cdot \sigma $ равно $s(D_ { xy } )$, если $\cos \gamma \geqslant 0$ { или, что то же самое, угол $\gamma $ - острый; проекция $\bar { n } (M)$ на орт $\bar { k } $ оси $\mathbf { \textit { Oz } } $ положительна } . Этот случай соответствует верхнему рисунка.

Соответственно, $\cos \gamma \cdot \sigma $ равно $-s(D_ { xy } )$, если $\cos \gamma <0$ { или, что то же самое, угол $\gamma $ - тупой; проекция $\bar { n } (M)$ на орт $\bar { k } $ оси $\mathbf { \textit { Oz } } $ отрицательна } . Этот случай соответствует нижнему рисунку. Итак, можно записать $R(\cos \gamma \cdot \sigma )=\pm R\cdot s(D_ { xy } )$.

Аналогично изложенному, $P(\cos \alpha \cdot \sigma )=\pm P\cdot s(D_ { yz } )$, где следует взять знак "+", если угол $\alpha $ - острый, и "-", если этот угол тупой, и $Q(\cos \beta \cdot \sigma )=\pm Q\cdot s(D_ { xz } )$, где берётся знак "+", если угол $\beta $ - острый, и "-", если этот угол тупой; $D_ { yz } $ - проекция $\sigma $ на плоскость $\mathbf { \textit { Oyz } } $, $D_ { xz } $ - проекция $\sigma $ на плоскость $\mathbf { \textit { Oxz } } $. Окончательно, $\Pi =\pm P\cdot s(D_ { yz } )\pm Q\cdot s(D_ { xz } )\pm R\cdot s(D_ { xy } )$.

Пусть теперь $\sigma $ - произвольная гладкая ограниченная поверхность, и скорость $\bar { v } (M)$ может меняться от точки к точке. Чтобы свести этот случай к предыдущему, разобьём $\sigma $ сетью кривых на $n$ частей $\sigma _1 ,\sigma _2 ,\ldots \sigma _i ,\ldots \sigma _n $, на каждой из частей $\sigma _i $ выберем произвольную точку $M_i $, и, считая, что $\sigma _i $ - плоская область, скорость $v\bar { ( } M)$ по $\sigma _i $ постоянна и равна $\bar { v } (M_i )$ и что ориентация всей части $\sigma _i $ характеризуется единичным нормальным вектором $\bar { n } (M_i )$, получим, что через $\sigma _i $ в единицу времени протекает $\Pi _i =\bar { v } (M_i )\bar { n } (M_i )\sigma _i $ жидкости { $i=1,2,\ldots ,n$ } .

Как мы видели, это выражение можно представить и в виде $\Pi _i =\bar { v } (M_i )\bar { n } (M_i )\sigma _i =f(M_i )\sigma _i $ { где $f(M_i )=\left| { \bar { v } (M_i ) }\right|\cdot \cos \varphi (M_i ), \varphi (M_i )$ - угол между $\bar { n } (M_i )$ и $\bar { v } (M_i ))$, и в виде $\prod_ { i } =\pm P(M_ { i } )\cdot s( { D_ { i } } _ { yz } )\pm Q(M_i)\cdot s( { D_ { i } } _ { xz } )\pm R(M_i)\cdot s( { D_ { i } } _ { xy } )$.

Суммируя эти выражения по всем $n$ дугам, получим выражения двух интегральных сумм: $\sum\limits_ { i=1 } ^n { f(M_i )\cdot \sigma _i } $ и $\sum\limits_ { i=1 } ^n { \left[ { \pm P(M_i )\cdot s( { D_i } _ { yz } )\pm Q(M_i )\cdot s( { D_i } _ { xz } )\pm R(M_i )\cdot s( { D_i } _ { xy } ) }\right] } $.

Переход к пределу в этих интегральных суммах при $\mathop { \max } \limits_ { i = 1,2,\ldots , n } diam (\sigma i )\rightarrow 0$ приведёт к двум поверхностным интегралам: $\iint\limits_\sigma { f(M)\cdot d\sigma } $ и $\iint\limits_\sigma { \pm P(M)ds_ { yz } \pm Q(M)ds_ { xz } \pm R(M)ds_ { xy } } $

Первый из этих интегралов называется поверхностным интегралом первого рода, или поверхностным интегралом по площади поверхности. Во втором интеграле элементы площади в координатных плоскостям принято записывать так, как мы это делали в двойном интеграле: $ds_ { yz } =dydz,ds_ { xz } =dxdz,ds_ { xy } =dxdy$ и опускать знаки перед слагаемыми: $\iint\limits_\sigma { P(M)dydz+Q(M)dxdz+R(M)dxdy } $ - этот интеграл называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам. Как и криволинейные интегралы двух родов, это разные объекты. Они имеют разные определения и разные свойства. В частности, поверхностный интеграл первого рода не зависит от ориентации поверхности, так как угол $\phi$ входит в подынтегральную функцию в явном виде, в то время как поверхностный интеграл второго рода меняет знак при изменении стороны поверхности { вектор $\bar { n } (M)$ меняется на $-\bar { n } (M)$ } .